Программная реализация цифрового регулятора

СКОРОСТИ И МОДЕЛИРОВАНИЕ КОНТУРА СКОРОСТИ

УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ

НЕПРЕРЫВНЫХ СТАЦИОНАРНЫХ СИСТЕМ

В современной теории управления широко применяется метод пространства состояний, который базируется на математических моделях в переменных состояния [5, 6, 8, 9, 11, 13, 15, 16]. Такая математическая модель представляет собой систему уравнений первого порядка, которую обычно представляют в векторно-матричной форме. Преимущество такого представления заключается в том, что облегчается решение задач анализа и синтеза с применением ЦВМ на этапе проектирования.

Динамические свойства линейной непрерывной стационарной системы описываются векторно-матричными уравнениями

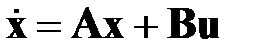, (4.1)

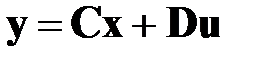,(4.2)

где х^T=[x₁ x₂ . . . x_n] – вектор-состояния размерности (n´1);

u^T=[u₁ u₂ . . . u_m] – вектор-входа размерности (m´1);

y^T=[y₁ y₂ . . . y_q] – вектор-выхода размерности (q´1);

A, B, C и D – матрицы коэффициентов размерности (n´n), (n´m), (q´n), (q´m), соответственно.

Уравнение (4.1) связывает переменные состояния и входные переменные и называется уравнением состояния. Уравнение (4.2) связывает выходные переменные с переменными состояния и входными переменными, и называется уравнением выхода.

На рис. 4.1 изображена векторная структурная схемалинейной непрерывной стационарной системы, построенная по уравнениям (4.1) и (4.2).

y

x

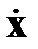D

С

А

В

s-1

u

Рис. 4.1. Векторная структурная схема

Из схемы следует, что на выходе интегратора (s^{– 1}) формируется вектор состояниях. Матрица Aназывается основной матрицейсистемы. B –матрица связи вектора входа системы с переменными состояния. C –матрица связи переменных состояния с вектором выхода системы. D – матрица связи вектора входа с вектором выхода.

СТРУКТУРНЫЕ СХЕМЫ МОДЕЛИРОВАНИЯ

ЦИФРОВЫХ СИСТЕМ

Применительно к цифровым системам управления используют структурные схемы моделирования, которые называются схемами программирования[6, 13, 15]. На основании схем программирования получают разностные уравнения цифровых регуляторов в векторно-матричной форме. Уравнения являются основой рабочей программы, которая может быть реализована в виде вычислительной процедуры микропроцессора.

Основное отличие схем моделирования цифровых систем от непрерывных заключается в наличии элемента задержки. Элемент задержки в преобразовании Лапласа представляется звеном запаздывания 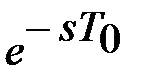, что соответствует степени z^–1 в теории z-преобразовании. Поэтому в структурных схемах моделирования цифровых систем вместо интегрирующего звена s^–1 будет стоять элемент задержки z^–1. При этом переход от непрерывной модели к цифровой осуществляется заменой в соответствии с формулой трапеций:

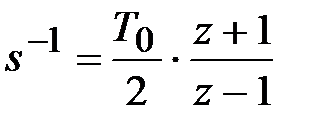, (4.3)

где Т₀ – период квантования.

Переход с применением формулы трапеций от аналоговой модели регулятора к цифровой будем называть дискретной аппроксимацией регулятора.

Большинство корректирующих устройств ЭП традиционно выполняются в виде аналоговых регуляторов, поэтому с целью модернизации на этапе проектирования решается задача замены аналогового регулятора цифровым. После проверки соответствия показателей качества синтезированного ЭП требованиям задания, выполняется дискретная аппроксимация аналогового регулятора и получение передаточной функции цифрового регулятора для обеспечения возможности перепрограммирования с целью улучшения качества управления.

Далее выполняются следующие операции:

- моделирование синтезированного ЭП с цифровым регулятором и уточнение периода квантования с применением прикладной программы MatLab;

- составление структурной схемы программирования и определение разностных уравнений цифрового регулятора;

Модель цифрового регулятора в переменных состояния описывается векторно-матричными уравнениями следующего вида:

X[(k +1) Т₀] = AX(kТ₀) + BDU(kТ₀);

U_цр(kТ₀) = СX(kТ₀) + DDU(kТ₀),

где U_цр(kТ₀) – вектор выходного сигнала цифрового регулятора;

DU(kТ₀) – вектор входного сигнала рассогласования.

Непосредственное программирование.Передаточная функция цифрового регулятора имеет вид:

.

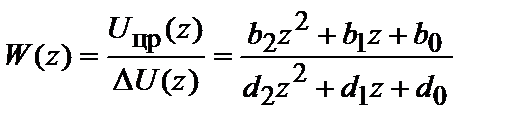После преобразования будем иметь:

.

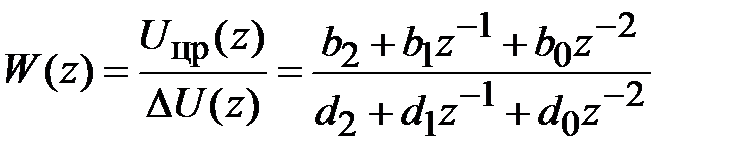Перепишем последнее выражение в виде:

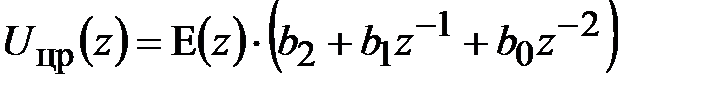, (4.4)

где

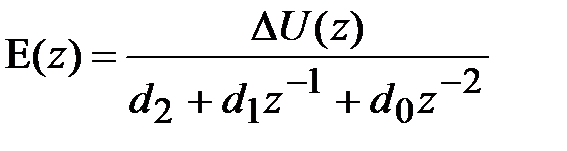. (4.5)

По выражениям (4.4) и (4.5) находим:

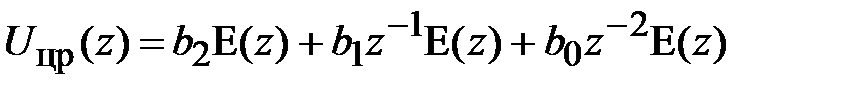, (4.6)

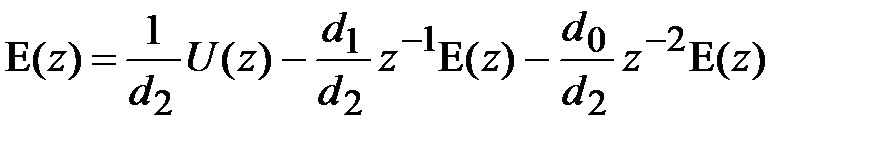. (4.7)

Уравнения (4.6) и (4.7) реализуются в виде структурной схемы непосредственного программирования, которая изображена на рис. 4.2.

Рис. 4.2. Структурная схема непосредственного программирования

В качестве переменных состояния системы принимаем выходные сигналы элементов задержки х₁(kT₀) и х₂(kT₀). По схеме (рис. 4.2) составляем уравнения состояния:

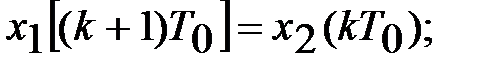
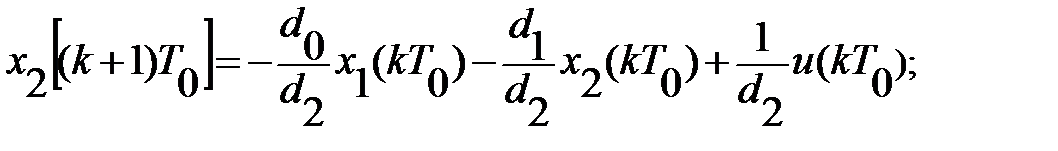
и уравнение выхода системы

.

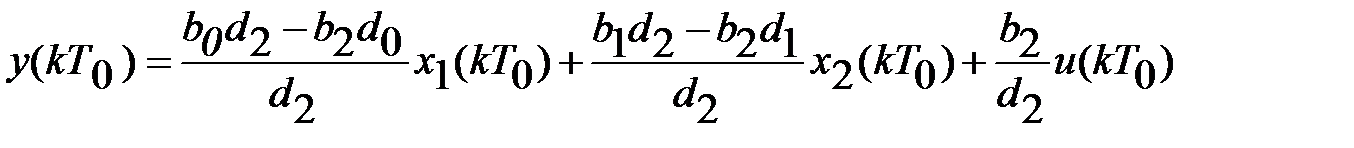Окончательно

.

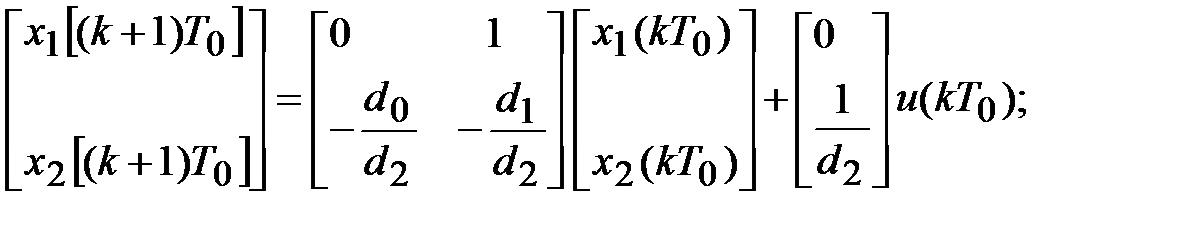
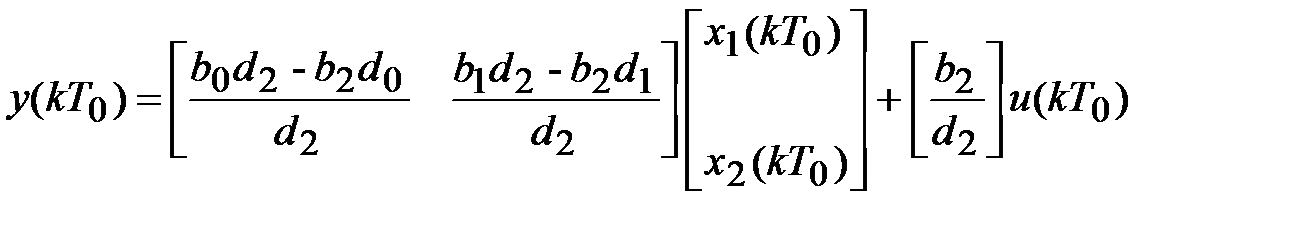Последовательное программирование. Передаточная функция цифрового регулятора записывается в виде произведения:

.

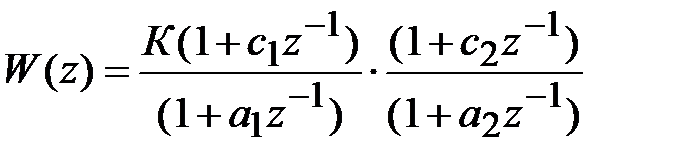Применяя к сомножителям преобразование (4.4) получаем структурную схему в переменных состояния, изображенную на рис. 4.3.

Рис. 4.3. Структурная схема последовательного программирования

Из схемы находим уравнения состояния и выхода системы в векторно-матричной форме

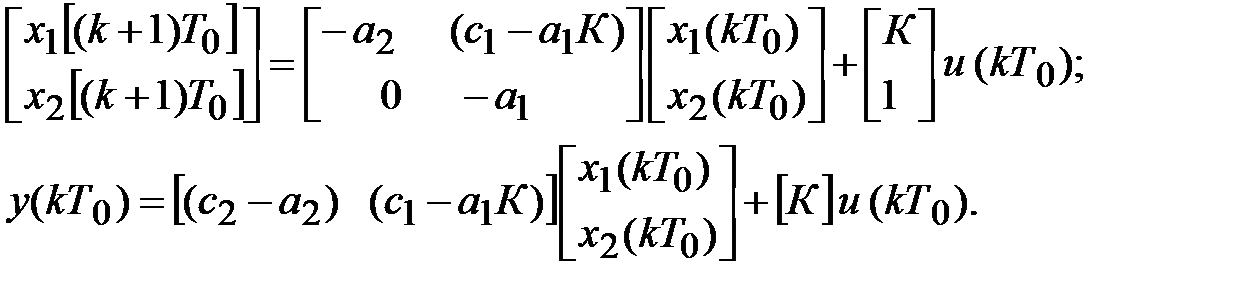
Параллельное программирование. Представим передаточную функцию цифрового регулятора в виде суммы передаточных функций

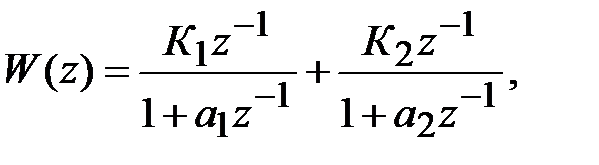(4.8)

где К₁, К₂ зависят от а₁, а₂и к и вычисляются в результате разложения (4.8) на элементарные дроби.

Структурная схема параллельного программирования, составленная непосредственно по слагаемым выражения (4.8) показана на рис. 4.4.

Рис. 4.4. Структурная схема параллельного программирования

Обозначив выходные сигналы элементов задержки символами переменных состояния x₁(kT₀) и x₂(kT₀),получаем:

;

.

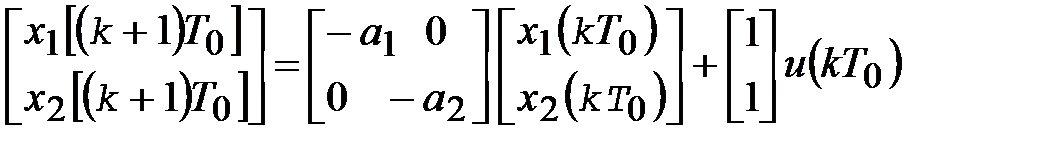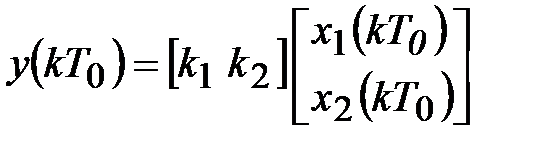Диагональные элементы основной матрицы уравнений состояния являются полюсами заданной передаточной функции, что подтверждает правильность составления уравнений по схеме, показанной на рис. 4.4.

ПРЕОБРАЗОВАНИЕ

υ-преобразование предполагает применение хорошо зарекомендовавших себя в инженерной практике методов анализа и синтеза непрерывных систем [2, 9] и позволяет с помощью замены

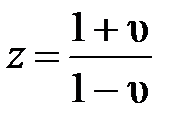(4.15)

перейти к характеристическому уравнению относительно новой переменной υ. Причем, комплексная υ-плоскость корней характеристического уравнения

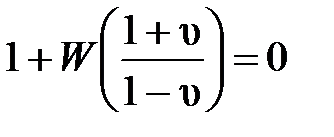
позволяет использовать критерии устойчивости, используемые для непрерывных систем.

Действительно, если ЦСУ устойчива, то в выражении (4.9) модуль числителя должен быть меньше модуля знаменателя.

Правомочность приведённых рассуждений иллюстрируется расположением вектора υ на рис. 4.5.

Рис. 4.5. υ-плоскость

Поскольку 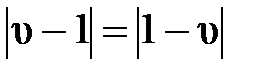, то длина вектора υ + 1 меньше длины вектора υ – 1 и тогда, согласно (4.15), модуль z будет меньше единицы и левая половина υ-плоскости будет областью устойчивости.

Аналогичное рассуждение можно привести также и для правой половины υ-плоскости, в которой (см. рис. 4.5) длина вектора υ + 1 всегда больше длины вектора υ – 1 и z по модулю больше единицы, что соответствует неустойчивой системе. Наконец, мнимая ось υ-плоскости является границей устойчивости, поскольку длины векторов υ + 1 и υ – 1 равны и .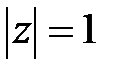

Наибольший практический интерес представляет применение логарифмических амплитудно-частотных и фазочастотных характеристик с использованием такого понятия, как псевдочастота. Для определения псевдочастоты рассмотрим -преобразование (4.15) и выделим из него комплексную переменную . Тогда

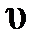
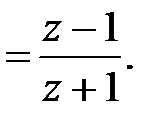
Полагая, что 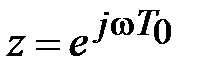, имеем

.

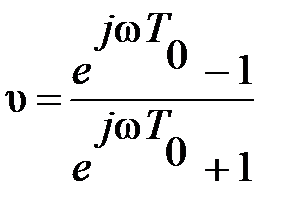Домножив числитель и знаменатель последнего выражения на степень 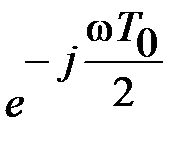, получим

,

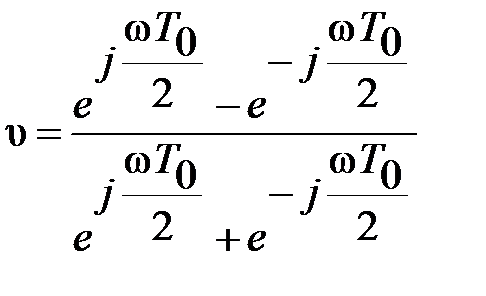После преобразований с применением формулы Эйлера можно записать, что

,

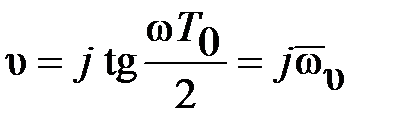где 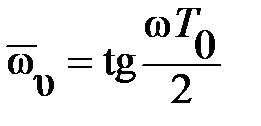– относительная псевдочастота;

Удобнее использовать абсолютную псевдочастоту

,

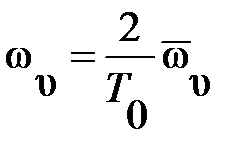которая имеет размерность с^{– 1}.

При малых частотах

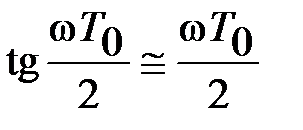
и абсолютная псевдочастота

.

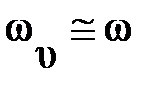При изменении частоты w в пределах от 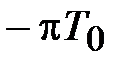до 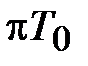псевдочастота 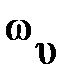изменяется от – ¥ до +¥.

Таким образом, для построения логарифмических частотных характеристик необходимо в дискретной передаточной функции разомкнутой ЦСУ W(z) сделать подстановку (4.9), получить

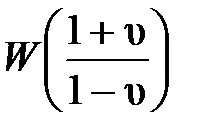
и перейти к псевдочастоте w_υ:

.
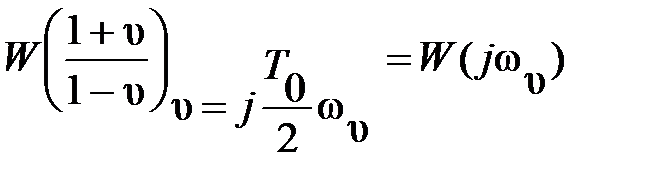