Дальнейшие свойства определенного интеграла

Вычисление определенного интеграла по формуле

Ньютона-Лейбница

Вычисление определенного интеграла, как предела интегральных сумм, сложно даже для простейших функций. Необходим простой способ вычисления определенных интегралов, минуя отыскание интегральных сумм и переход к пределу. Этот метод, основанный на связи определенного интеграла с вычислением первообразной, выражается формулой Ньютона-Лейбница.

Теорема. Пусть функция 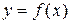непрерывна на отрезке 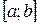и F(x) –

любая первообразная для f(x) на 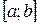. Тогда определенный инте-

грал от функции f(x) на 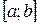равен приращению первообразной

F(x) на этом отрезке:

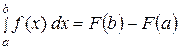. (25)

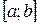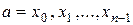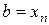
Доказательство.Разобьем отрезок точками , 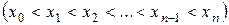на n-частичных отрезков 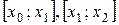, …, 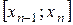(рисунок 10).

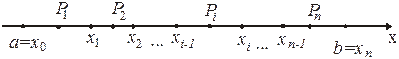
Рисунок 10

Рассмотрим тождество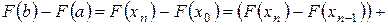

.

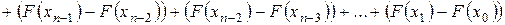Преобразуем каждую разность в скобках по теореме Лагранжа

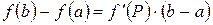. (26)

Получаем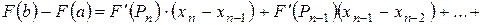

;

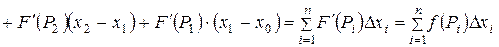следовательно, 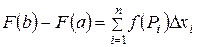, (27)

где 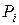есть некоторая точка интервала .

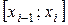Так как функция 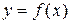непрерывна на 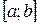, то она интегрируема на 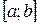. Поэтому существует предел интегральной суммы, равный определенному интегралу от 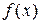на .

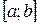Переходя в равенстве (27) к пределу при 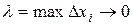, получаем

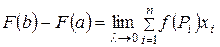, т.е. .

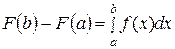Равенство (25) называется формулой Ньютона-Лейбница.

Если ввести обозначения 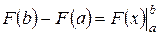, то формулу Ньютона-Лейбница (25) можно переписать в виде: .

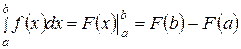Читается формула (25) так: чтобы вычислить определенный интеграл от непрерывной функции f(x) на отрезке 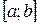, надо найти ее первообразную функцию 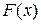и взять разность значений этой первообразной на концах отрезка : .

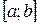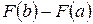Замечание 1. Мы ввели понятие 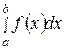для случая 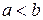. Его можно обобщить и на случай 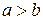. Сделаем это так, чтобы формула Ньютона-Лейбница оставалась справедливой.

Положим, по определению, что для 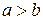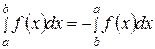. (28)

Проверим справедливость формулы Ньютона-Лейбница:

.

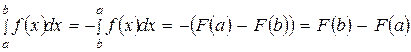Принимая во внимание (28), для нас отныне будет несущественно, какой из пределов интегрирования больше: верхний или нижний.

Эта формула имеет место и для : .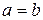

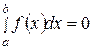Замечание 2. Величина интеграла 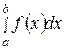не зависит от того, какой буквой обозначена переменная интегрирования, т.е. 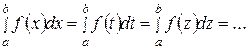, а зависит лишь от вида подынтегральной функции и отрезка интегрирования, поскольку смена обозначений такого рода никак не влияет на поведение интегральной суммы.

Формула Ньютона-Лейбница дает практически удобный метод вычис­ления определенных интегралов в том случае, когда известна первообразная подынтегральной функции.

Только с открытием этой формулы определенный интеграл смог полу­чить то значение в математике, какое он имеет в настоящее время. Эта фор­мула значительно расширила область применения определенного интеграла, так как математика получила общий метод для решения различных задач ча­стного вида и поэтому смогла значительно расширить круг приложений оп­ределенного интеграла.

Пример 10. Вычислить определенные интегралы: а) 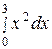; б) ;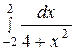

в) .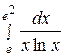

Решение. а) .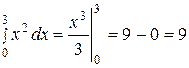

б) .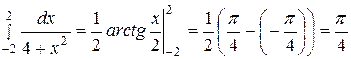

в) .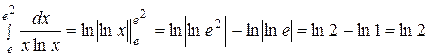

Пример 11. Найти массу прямолинейного стержня 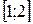, плотность которого в каждой точке 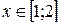равна .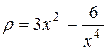

Решение. По формуле (21) имеем: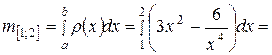

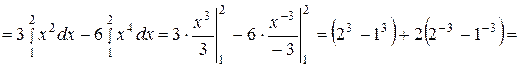
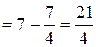(ед.массы).

Дальнейшие свойства определенного интеграла

2.1. Теорема о среднем. Если функция 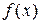непрерывна на отрезке 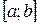, то существует точка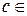 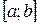такая, что

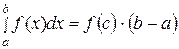. (29)

Доказательство. По формуле Ньютона-Лейбница имеем 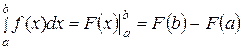, где .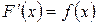

Применяя к разности 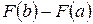теорему Лагранжа, получим .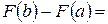

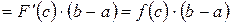Теорема о среднем при 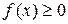имеет простой геометрический смысл: значение определенного интеграла равно, при некотором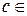 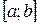, площади прямоугольника с высотой 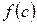и основанием 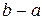(рисунок 11). Число

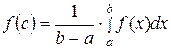(30)

называется средним значением функции 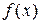на отрезке .

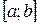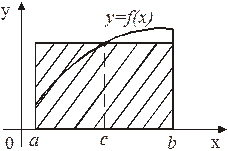
Рисунок 11

2.2 Свойство неотрицательности.

Если функция 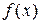сохраняет знак на отрезк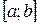е , где 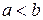, то интеграл 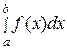имеет тот же знак, что и функция:

если 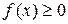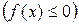на отрезке 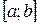, то

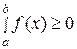
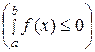. (31)

Доказательство. По теореме о среднем 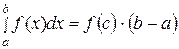, где .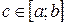

Так как 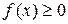для всех 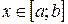, то и 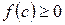, а 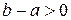, поэтому 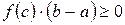, т.е. 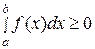, что требовалось доказать.

2.3. Неравенство между непрерывными функциями на отрезке 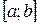, 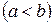можно почленно интегрировать.

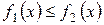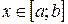Если при , то

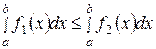. (32)

Доказательство. Так как 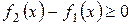, то при 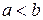согласно свойству 6 имеем 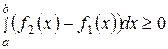, а по свойству 2 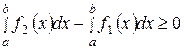, т.е.

.

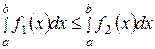Оценка интеграла.

Если m и М – соответственно наименьшее и наибольшее значения функции 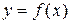на отрезке 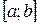, ( 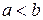), то

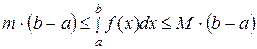. (33)

Доказательство. Так как для любого 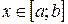имеем 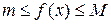, то, согласно свойству 7, имеем .

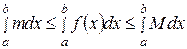Применяя к крайним интегралам свойства 1 и 4, получаем

.

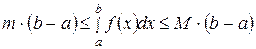Если 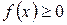, то свойство 8 иллюстрируется геометрически: площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых есть отрезок 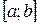, а высоты равен m и М соответственно (рисунок 12).

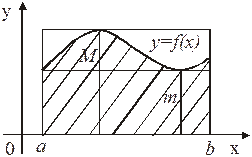
Рисунок 12

2.5. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции:

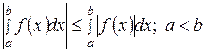. (34)

Доказательство. Применяя свойство 7 к очевидным неравенствам 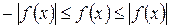, получаем .

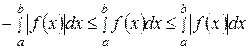Отсюда, по определению модуля, следует, что .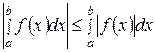

2.6. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, т.е.:

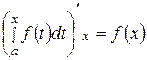. (35)

Доказательство. По формуле Ньютона-Лейбница имеем: 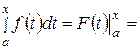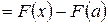. Следовательно, .

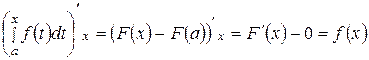Это обозначает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.

Методы интегрирования

Для нахождения определенного интеграла применяют методы интегрирования, аналогичные методам интегрирования в неопределенном интеграле. Рассмотрим основные из них.