Задачи для решения в аудитории
Занятие №2
Дифференциальные уравнения 1-го порядка (2).
Необходимые сведения.
- Уравнения с разделяющимися переменными.Метод разделения переменных:
Если ДУ имеет вид (или может быть приведено к такому виду): 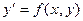 ,
,
где 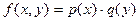 , то оно называется ДУ с разделяющимися переменными.
, то оно называется ДУ с разделяющимися переменными.
Тогда 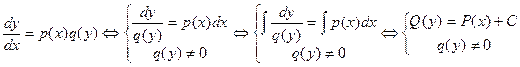
Отдельно следует проверить, не является ли интегралом ДУ выражение 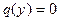 .
.
Если ответ положителен, то это выражение следует добавить к полученному решению.
- Уравнения, приводящиеся к уравнениям с разделяющимися переменными.
Уравнения вида 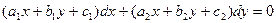 при
при 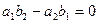 допускают разделение переменных, если произвести линейную замену
допускают разделение переменных, если произвести линейную замену 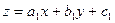 или
или 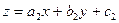
- Уравнения с однородной правой частью и приводящиеся к ним.
- Если ДУ имеет вид (или может быть приведено к такому виду):
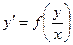 , то оно называется ДУ с однородной правой частью.
, то оно называется ДУ с однородной правой частью.
Оно сводится к уравнению с разделяющимися переменными заменой:
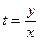
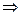
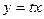
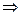
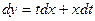 или
или 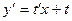
- Уравнение вида
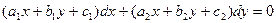 при
при 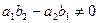 сводятся к однородному, если перенести начало координат в точку пересечения прямых
сводятся к однородному, если перенести начало координат в точку пересечения прямых
 и
и 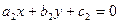 ,
,
т.е. заменой 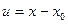 ,
, 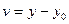 , где
, где 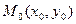 - точка пересечения прямых.
- точка пересечения прямых.
- Некоторые уравнения вида
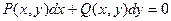 , где P и Q не являются однородными функциями одного порядка сводятся к однородному заменой
, где P и Q не являются однородными функциями одного порядка сводятся к однородному заменой 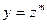 .
.
- Линейные ДУ I , уравнения Бернулли и уравнения Риккати.
- Уравнение вида
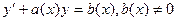 называется линейным уравнением 1-го порядка.
называется линейным уравнением 1-го порядка.
Структура общего решения такого уравнения: 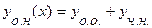 ,
,
где 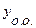 – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения 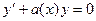 ,
,
а 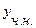 – частное решение данного неоднородного.
– частное решение данного неоднородного.
Общее решение однородного легко находится, т.к. переменные разделяются, и оно имеет вид: 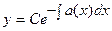 . Общее решение неоднородного ищется в виде
. Общее решение неоднородного ищется в виде 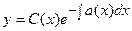 .
.
- Уравнение Бернулли – это уравнение вида:
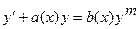
Оно сводится к линейному заменой: 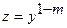 .
.
- Уравнение Риккати – это уравнение вида:
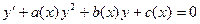
Оно сводится к уравнению Бернулли заменой 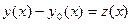 , где
, где 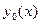 - какое-то решение уравнения Риккати
- какое-то решение уравнения Риккати
- Уравнения в полных дифференциалах.
- Уравнение вида
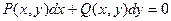 , заданное в области D, называется уравнением в полных дифференциалах, если
, заданное в области D, называется уравнением в полных дифференциалах, если 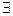 такая непрерывная в D функция
такая непрерывная в D функция 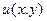 , что левая часть уравнения есть полный дифференциал этой функции (
, что левая часть уравнения есть полный дифференциал этой функции ( 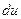 ).Тогда решение
).Тогда решение 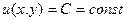 .
.
Достаточным условием того, что уравнение является ур-нием в полных дифференциалах, служит равенство: 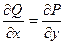
Дифференциальные уравнения 2 курс 3-ий семестр.
Задачи для решения в аудитории.
1. Найти решения уравнений, удовлетворяющих заданному начальному условию (НУ):
1.1. 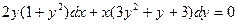 , НУ:
, НУ: 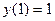
1.2 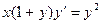 , НУ:
, НУ: 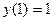
1.3 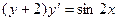 , НУ:
, НУ: 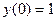
2. С помощью линейной замены переменных привести уравнение к уравнению с разделяющимися переменными и найти общее решение:
2.1. 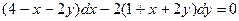
3. Найти общее решение уравнений:
3.1 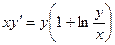 3.2
3.2 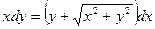 3.3
3.3 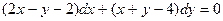
3.4 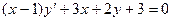 3.5
3.5 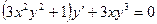
4. Найти общее решение линейного ДУ I
· методом вариации произвольной постоянной (Лагранжа):
4.1 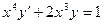 4.2
4.2 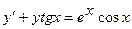
· не применяя метод Лагранжа (с помощью искусственного приёма):
4.3 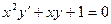
5. Найти ортогональные траектории семейства кривых 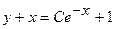 .
.
6. Решить уравнения, сводя их к линейным:
6.1 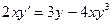 (Бернулли)
(Бернулли)
6.2 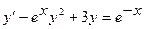 (Риккати)
(Риккати)
Домашнее задание.
1. 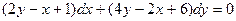 2.
2. 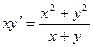 3.
3. 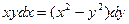
4. 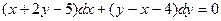 5.
5. 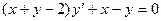
6. 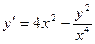 7.
7. 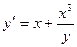 8.
8. 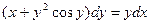
9. 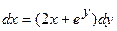 10.
10. 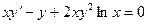
11. 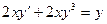 12.
12. 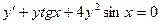
13. 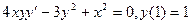 14.
14. 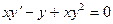 15.
15. 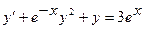
Дополнительно: Задачи для подготовки к контрольной работе, защите т.р., экзамену:
1.Сб.задач по ДУ Филиппова: №№ 51-65, 101-129, 137-160,186-194
2.Сб.задач по ДУ Романко: №№ 1-51 (стр.12-13), 57-87(стр.14-15),1-95 (стр.20-23), 1-18 (стр.28-29)
3.Сб.задач Ефимов-Поспелов т.2: №№ 10.22-10.105,10.130-10.164.
