Дифференциальные уравнения теплообмена

В общем случае теплообмен определяется не только тепловыми, но и гидродинамическими явлениями. Поэтому математическое описание задач теплообмена включает в себя дифференциальные уравнения:

· энергии;

· теплоотдачи;

· движения;

· неразрывности,

а также условий однозначности, конкретизирующих ту или иную задачу.

Дифференциальное уравнение температурного поля движущейся жидкости – уравнение энергии(1.12) – приведено в разделе 1.

Уравнение теплоотдачи. При обтекании вязкой жидкостью твердой поверхности скорость жидкости на ней равна нулю. Это условие «прилипания» вязкой жидкости является следствием того, что между поверхностью твердого тела и жидкостью действуют силы молекулярного сцепления, в результате чего прилегающий к твердой стенке слой жидкости становится неподвижным и теплота через этой слой передается только теплопроводностью

.

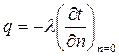С другой стороны, этот же тепловой поток определяется уравнением Ньютона-Рихмана

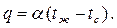
Приравняв правые части равенств, получим дифференциальное уравнение теплоотдачи

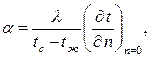(6.1)

из которого следует, что для определения коэффициента теплоотдачи необходимо найти температурный градиент среды вблизи поверхности. Температурный градиент может быть найден из дифференциального уравнения энергии (1.12). В уравнение (1.12) входят составляющие скорости (w_x, w_y , w_z), которые требуют дифференциального уравнения, позволяющего найти поле скоростей, – уравнения движения.

Уравнение движения. В классической гидродинамике уравнение движения вязкой несжимаемой жидкости (уравнение Навье – Стокса) для стационарного режима в проекции на ось ох имеет вид

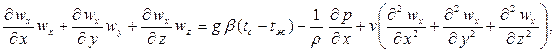(6.2)

где w_x – проекция вектора скорости на ось ох; g=9,8 м/с² ; 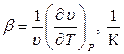- температурный коэффициент объемного расширения; r, кг/м³ – плотность;
р, Па – давление; v, м²/с – кинематическая вязкость.

Левая часть уравнения (6.2) характеризует инерционные силы потока жидкости, первое слагаемое правой части определяет подъемную силу, возникающую вследствие разности плотностей холодных и нагретых объемов жидкости, второе слагаемое – действие сил давления, третье – сил вязкого трения.

Аналогичные уравнения в проекции на оси оy, оz обозначим номерами (6.3), (6.4).

Анализ уравнений (1.12), (6.1) – (6.4) показывает, что для решения задачи конвективного теплообмена к перечисленным выше уравнениям необходимо добавить еще одно – уравнение неразрывности потока.

Уравнение неразрывности. Применение закона сохранения массы к элементарному объему несжимаемой жидкости дает дифференциальное уравнение неразрывности

.

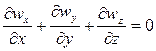(6.5)

Условия однозначности включают:

· геометрические условия (форму и размеры поверхности соприкосновения с жидкостью);

· физические условия (теплопроводность, вязкость и др. свойства жидкости);

· граничные условия (распределение скоростей и температур на границах рассматриваемой системы).

Для некоторых задач теплообмена могут быть получены и более сложные системы дифференциальных уравнений и условий однозначности.

Решение системы дифференциальных уравнений конвективного теплообмена возможно при введении упрощающих предположений для некоторых случаев теплоотдачи. Однако принятые допущения требуют сопоставления аналитических решений с результатами эксперимента.

В ряде случаев система дифференциальных уравнений конвективного теплообмена решается численными методами с применением ЭВМ.

В большинстве же случаев единственным способом получения уравнения для расчета коэффициента теплоотдачи является физический эксперимент с обработкой данных на основе теории подобия физических явлений.

Основы теории подобия

Теория подобия – учение о подобных явлениях. Она позволяет на основе дифференциальных уравнений и условий однозначности создать теоретическую базу для постановки опытов и обработки их результатов.

Понятие подобия впервые было введено в геометрии, но оно распространяется и на физические явления. Последние считаются подобными, если они относятся к одному и тому же классу, протекают в геометрически подобных системах и подобны все однородные физические величины, характеризующие эти явления.

Для подобных физических явлений в сходственных точках и в сходственные моменты времени любая величина φ¢ первого явления пропорциональна величине j¢¢ второго явления: φ¢=С_φ ∙ φ¢¢, где С_φ – константа подобия. Два промежутка времени τ′ и τ" называются сходственными, если они имеют общее начало отсчета и связаны равенством τ′ / τ"=С_τ=const. При геометрическом подобии выполняется равенство

х′ / х"=у' / у"=z' / z"= 1' / 1" = 2' / 2 "=C .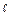

При кинематическом подобии имеет место подобие скоростей w′/w′′=C_w, при динамическом – подобие сил давления р′ /р"=С_Р , при тепловом – подобие температурных полей t'/t"=C_t .

Для физических явлений, определяемых множеством параметров, константы подобия этих параметров связаны между собой и не могут быть выбраны произвольно.

Уравнения, описывающие подобные физические явления, после приведения их к безразмерному виду становятся тождественными, при этом в сходственных точках все одноименные безразмерные величины будут одинаковыми.

Приведение к безразмерному виду системы дифференциальных уравнений конвективного теплообмена (1.12), (6.1) – (6.5) позволяет получить безразмерные комплексы, называемые числами подобия:

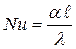- число Нуссельта, характеризует интенсивность конвективного теплообмена;

, м – геометрический размер;

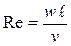- число Рейнольдса, характеризует отношение сил инерции к силам вязкости;

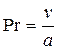- число Прандтля, характеризует теплофизические свойства жидкости;

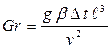- число Грасгофа, характеризует отношение подъемной силы, возникающей вследствие разности плотностей жидкости благодаря перепаду температур Δt, к силам вязкости;

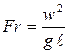- число Фруда, характеризующее отношение инерционных сил к силам тяжести, и т.д.

Число Нуссельта (Nu) является определяемым числом в задачах конвективного теплообмена, т.к. содержит искомую величину – коэффициент теплоотдачи a. Остальные числа подобия (Re, Pr, Gr, Fr…) называются определяющими и включают в себя величины, от которых зависит коэффициент теплоотдачи.

Таким образом,

Nu=f(Re, Pr, Gr, Fr…).

(6.6)

Функциональная зависимость между числами подобия типа (6.6) называется уравнением подобия. По уравнению подобия можно найти число Nu и рассчитать коэффициент теплоотдачи.

Основные положения теории подобия формулируются в виде трех теорем:

1. Подобные процессы должны иметь одинаковую физическую природу и описываться одинаковыми дифференциальными уравнениями.

2. Условия однозначности подобных процессов (геометрические, физические, граничные и т.д.) должны быть одинаковы во всем, кроме численных значений размерных постоянных.

3. Одноименные определяющие числа подобия подобных процессов должны иметь одинаковую численную величину (Re'=Re", Gr'=Gr" и т.д.).

Теорию подобия можно рассматривать как учение об обобщенных безразмерных переменных, характеризующих данный процесс.