Вычисление пределов. Бином Ньютона. Число e. Критерий Коши
Лекция №12!
1. Мы доказываем теорему о свойствах пределов. Пусть 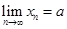 ,
, 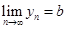 , тогда
, тогда 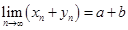 ,
, 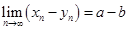 ,
, 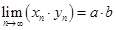 , а если, кроме того,
, а если, кроме того, 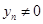 ,
, 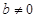 , то
, то 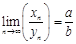 .
.
2. Доказательство формулы 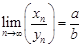 . Мы докажем, что предел частного последовательностей равен частному от их пределов, если каждый из пределов существует, все числа в знаменателе не равны 0 и предел знаменателя не равен 0. Так как
. Мы докажем, что предел частного последовательностей равен частному от их пределов, если каждый из пределов существует, все числа в знаменателе не равны 0 и предел знаменателя не равен 0. Так как 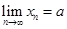 , то
, то 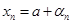 , где
, где 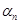 - б. м. Аналогично
- б. м. Аналогично 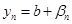 , где
, где 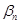 - б. м. Отсюда следует, что
- б. м. Отсюда следует, что 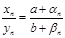 . Для доказательства формулы достаточно доказать, что величина
. Для доказательства формулы достаточно доказать, что величина 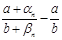 является б. м. Проверим, что величина
является б. м. Проверим, что величина 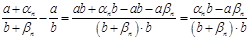 является б. м. В самом деле, легко проверить, что в полученном выражении числитель стремится к 0, а знаменатель по модулю больше некоторого положительного числа. Формула доказана.
является б. м. В самом деле, легко проверить, что в полученном выражении числитель стремится к 0, а знаменатель по модулю больше некоторого положительного числа. Формула доказана.
3. Теорема 1. Монотонная и ограниченная числовая последовательность имеет предел.
4. Мы знаем, что 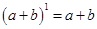 ,
, 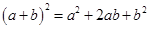 и т. д. Формула бинома Ньютона обобщает эти правила на случай произвольной степени.
и т. д. Формула бинома Ньютона обобщает эти правила на случай произвольной степени.
5. Теорема 2. Справедлива формула бинома Ньютона 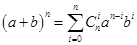 , (6) где
, (6) где 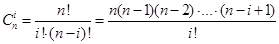 .
.
6. Доказательство. метод математической индукции. Если утверждение надо доказать для всех натуральных значений параметра 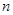 , то для этого достаточно доказать это утверждение для
, то для этого достаточно доказать это утверждение для 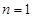 и затем доказать, что из справедливости утверждения для
и затем доказать, что из справедливости утверждения для 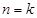 следует справедливость этого утверждения для
следует справедливость этого утверждения для 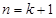 .
.
7. Проверим справедливость формулы (6) при 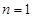 . Действительно,
. Действительно, 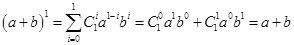 , т. к. (проверьте)
, т. к. (проверьте) 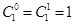 .
.
Пусть формула (6) справедлива при 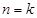 , т. е.
, т. е. 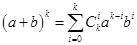 . Вычислим
. Вычислим 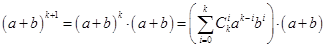 . Последнее произведение представляется в виде
. Последнее произведение представляется в виде 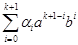 и при этом
и при этом 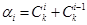 . С другой стороны, для проверки индуктивного предположения надо доказать, что
. С другой стороны, для проверки индуктивного предположения надо доказать, что 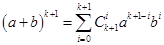 . Следовательно, для завершения доказательства теоремы Ньютона надо установить справедливость соотношения
. Следовательно, для завершения доказательства теоремы Ньютона надо установить справедливость соотношения 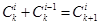 . Действительно,
. Действительно, 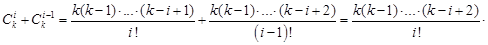
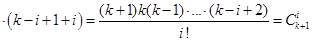 . Теорема доказана.
. Теорема доказана.
8. Кстати, величина 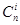 называется числом сочетаний из
называется числом сочетаний из 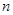 по
по 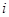 и показывает, сколькими способами можно выбрать
и показывает, сколькими способами можно выбрать 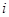 предметов из
предметов из 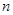 предметов.
предметов.
9. Теорема 3. Для членов числовой последовательности (7) справедливы соотношения: 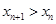 ,
, 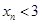 .
.
10. Доказательство. Для величины 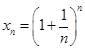 применим формулу бинома Ньютона. Следовательно,
применим формулу бинома Ньютона. Следовательно, 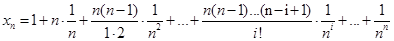 и отсюда
и отсюда 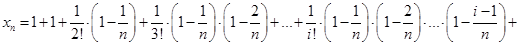
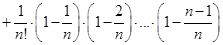 . Мы видим, что с ростом
. Мы видим, что с ростом 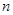 каждое слагаемое в последней записи
каждое слагаемое в последней записи 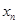 и число слагаемых увеличиваются. Следовательно,
и число слагаемых увеличиваются. Следовательно, 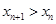 . Для доказательства второй части теоремы заметим, что
. Для доказательства второй части теоремы заметим, что 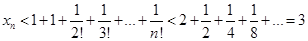 . Теорема доказана.
. Теорема доказана.
11. Теорема 4. (Больцано-Вейерштрассе) Каждая ограниченная последовательность содержит сходящуюся подпоследовательность.
12. Теорема 5. (Критерий Коши) Числовую последовательность 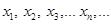 (1) сходится тогда и только тогда, когда выполнен следующий критерий:
(1) сходится тогда и только тогда, когда выполнен следующий критерий: 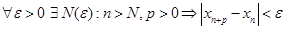 (10)
(10)
13. Доказательство. Необходимость. Достаточность.
Лекция №13!
1. Функция 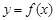 называется четной функцией, если для всех
называется четной функцией, если для всех 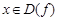 определено значение функции
определено значение функции 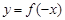 и выполнено равенство
и выполнено равенство 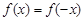 .
.
2. Функция 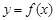 называется нечетной функцией, если для всех
называется нечетной функцией, если для всех 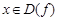 определено значение функции
определено значение функции 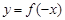 и выполнено равенство
и выполнено равенство 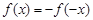 .
.
3. Число 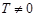 называется периодом функции
называется периодом функции 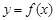 , если для всех
, если для всех 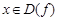 определено значение функции
определено значение функции 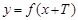 и выполнено равенство
и выполнено равенство 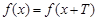 . Наименьшее положительное
. Наименьшее положительное 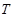 , удовлетворяющее этому условию, называется основным периодом функции
, удовлетворяющее этому условию, называется основным периодом функции 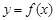 (если нет двусмысленности, то иногда просто периодом функции).
(если нет двусмысленности, то иногда просто периодом функции).
4. Множество точек вида 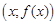 , где
, где 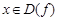 называется графиком функции
называется графиком функции 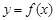 . Если функция четная, то ее график функции симметричен относительно оси ординат. Если функция нечетная, то ее график функции симметричен относительно начала координат.
. Если функция четная, то ее график функции симметричен относительно оси ординат. Если функция нечетная, то ее график функции симметричен относительно начала координат.
