Треугольник Паскаля. Бином Ньютона

В течение всех лет обучения в школе мы много решаем разнообразных задач, в том числе и логических: задачи занимательного характера, головоломки, анаграммы, ребусы и т.п. Чтобы успешно решать задачи такого вида, надо уметь выделять их общие признаки, подмечать закономерности, выдвигать гипотезы, проверять их, строить цепочки рассуждений, делать выводы. Логические задачи от обычных отличаются тем, что не требуют вычислений, а решаются с помощью рассуждений. Можно сказать, что логическая задача – это особая информация, которую не только нужно обработать в соответствии с заданным условием, но и хочется это сделать. Логика помогает усваивать знания осознанно, с пониманием, т.е. не формально; создаёт возможность лучшего взаимопонимания.

Логика – это искусство рассуждать, умение делать правильные выводы. Это не всегда легко, потому что очень часто необходимая информация «замаскирована», представлена неявно, и надо уметь её извлечь. Как известно, видение рождает мышление. Возникает проблема: как установить логические связи между разрозненными фактами и как оформить в виде единой целой. Видеть ход доказательства и решения задач позволяет метод граф - схем, который делает доказательство более наглядным и позволяет кратко и точно изложить доказательства теорем и решения задач.

Метод граф

Слово «граф» в математической литературе появилось совсем недавно. Понятие графа используется не только в математике, но и в технике и даже в повседневной жизни под разными названиями – схема, диаграмма.

Особенно большую помощь графы оказывают при решении логических задач. Представляя изучаемые объекты в наглядной форме, «графы» помогают держать в памяти многочисленные факты, содержащиеся в условии задачи, устанавливать связь между ними.

Графом называется любое множество точек, некоторые из которых соединены линиями или стрелками. Точки, изображающие элементы множества, называют вершинами графа, соединяющие их отрезки – рёбрами графа. Точки пересечения рёбер графа не являются его вершинами. Во избежание путаницы вершины графа часто изображают не точками, а маленькими кружочками. Рёбра иногда удобнее изображать не прямолинейными отрезками, а дугами.

Родившись при решении головоломок и занимательных игр ( задачи о шахматном коне, о ферзях, « кругосветное путешествие », задачи о свадьбах и гаремах и т.п. ), теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем.

Пример 1.1.Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?

Решение.Обозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке, а пунктирная, что не лежит. Тогда с учетом задачи имеем G1 (рис. 1).

Рис.1

Далее достраиваем граф по следующему правилу: поскольку в короб может лежать ровно один карандаш, то из каждой точки должны выходить одна сплошная линия и три пунктирные. Получается граф G2 , дающий решение задачи.

Пример 1.2.Беседуют трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: «Любопытно, что один из нас белокурый, другой брюнет, третий рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос имеет каждый из друзей?

Решение.Построим граф отношения, заданного в условии задачи. Для этого, прежде всего, выделим множество фамилий М и множество цветов волос К, элементы которых будем обозначать точками. Точки множества М назовем буквами Б, Ч, Р (Белокуров, Чернов и Рыжов); точки второго множества – б, бр, р (белокурый, брюнет, рыжий). Если точке из одного множества соответствует точка из другого, мы их соединим сплошной линией, а если не соответствует – штриховой. Условие задачи указывает лишь на несоответствия, поэтому вначале должен возникнуть граф, изображенный на рисунке 2.

Рис.2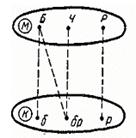

Из условия задачи следует, что для каждой точки из множества М существует одна и только одна точка из множеств К, которая соответствует первой и, наоборот, каждой точке из множества К соответствует одна и только одна точка из множества М. Задача сводится к тому, чтобы найти это единственно возможное соответствие между элементами множеств М и К, т. е. к нахождению трех сплошных линий, соединяющих соответствующие точки множеств.

Принцип решения задачи прост. Если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с его третьей точкой ее необходимо соединить сплошной линией. Поэтому граф на рисунке 2 дополняется сплошными линиями, соединяющими точки Б и р, Р и бр (рис. 3).

Рис.3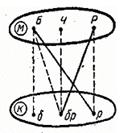

Далее остается соединить сплошной линией точку Ч и точку б, так как точка Ч соединена с точкой бр штриховой линией, а точка р уже «занята» (рис. 4).

Рис. 4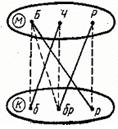

Таким образом, на графе этого рисунка автоматически прочитываем ответ: Белокуров — рыжий, Чернов — белокурый, Рыжов – брюнет.

В следующей задаче применение графов помогает обнаружить наличие двух решений.

Пример 1.3.Маша, Лида, Женя и Катя умеют играть на разных инструментах (виолончели, рояле, гитаре и скрипке), но каждая только на одном. Они же владеют разными иностранными языками (английским, французским, немецким и испанским), но каждая только одним. Известно, что:

1. девушка, которая играет на гитаре, говорит по-испански;

2. Лида не играет ни на скрипке, ни на виолончели и не знает английского языка;

3. Маша не играет ни на скрипке, ни на виолончели и не знает английского языка;

4. девушка, которая говорит по-немецки, не играет на виолончели;

5. Женя знает французский язык, но не играет на скрипке.

Кто на каком инструменте играет и какой иностранный язык знает?

Решение. Условию задачи соответствует граф, изображенный на рисунке 5.

Рис. 5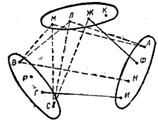

Проведем последовательно следующие сплошные отрезки: КС, ВЖ, ВФ, АК (рис.6).

Рис. 6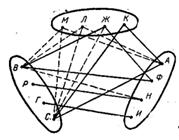

Тем самым образуются два «сплошных» треугольника ЖВФ и КСА. Проводим еще сплошной отрезок РН. Теперь убеждаемся, что условия задачи не обеспечивают однозначности выбора третьей точки для каждой из пар РН и ГИ. Возможны следующие варианты «сплошных» треугольников: МГИ и ЛРН или ЛГИ и МРН. Таким образом, задача имеет два решения.

Метод кругов Эйлера

Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.

Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги. Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры.

Пример 1.4.Часть жителей города умеет говорить только по-русски, часть – только по-узбекски и часть умеет говорить на обоих языках. По-узбекски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?

Решение.Составим схему.

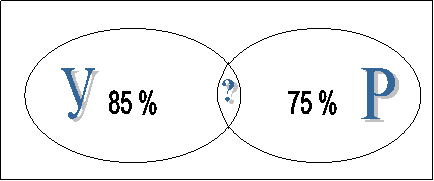
В кружке под буквой «У» обозначим жителей, говорящих по-узбекски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «У» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).

Общие правила комбинаторики

Решение многих комбинаторных задач основывается на двух фундаментальных правилах, называемых правилом суммы и правилом произведения. Прежде всего определимся в терминологии. Если имеется, к примеру, 5 шаров в ящике, то мы будем говорить, что один шар из ящика можно выбрать пятью способами.

Правило суммы. Если объект А можно выбрать n способами, а объект В-k способами, то объект "А или В" можно выбрать n+k способами.

Пример 2.1.В ящике находятся 20 шаров: 5 белых, 6 черных, 7 синих и 2 красных. Сколькими способами можно взять из ящика один цветной шар?

Решение.Здесь предполагается, что цветной шар - это синий или красный, поэтому надо применять правило суммы. Цветной шар можно выбрать 7 + 2 = 9 способами.

Правило произведения. Если объект А можно выбрать n способами, а объект В независимо от него - k способами, то пару объектов "А и В" можно выбрать n·k способами.

Пример 2.2.Сколько может быть различных комбинаций выпавших граней при бросании двух игральных костей? (Игральная кость - это кубик, на гранях которого нанесены числа 1, 2, 3, 4, 5, 6 )
Решение. На первой кости может выпасть 1, 2, 3, 4, 5 или 6 очков, то есть всего будет 6 вариантов. Точно так же и на второй кости 6 вариантов. По получится всего 6 · 6 = 36 способов. Правила суммы и произведения справедливы не только для двух, но и для любого числа объектов. Приведем еще несколько примеров, в которых необходимо выбрать правило суммы или произведения.

Пример 2.3.Из города А в город В ведут 5 дорог, а из города В в город С - 3 дороги. Сколькими способами можно проехать из города А в город С?
Решение. Чтобы проехать из А в С, надо проехать из А в В и из В в С, поэтому применим правило произведения. 5 · 3 = 15.

Пример 2.4. На книжной полке стоят 3 книги по алгебре, 4 книги по геометрии и 5 книг по литературе. Сколькими способами можно взять с полки одну книгу по математике?
Решение.Книга по математике - это книга по алгебре или по геометрии. Применяем правило суммы. 3 + 4 = 7.

Пример 2.5.В меню имеется 4 первых блюда, 3 вторых и 2 третьих. Сколько различных полных обедов можно из них составить?
Решение.Полный обед состоит из первого, и второго, и третьего блюд. По правилу произведения получаем 4 · 3 · 2 = 24 различных полных обеда.

Размещения

Если из данного множества предметов мы будем выбирать некоторое подмножество, то его будем называть выборкой. Выборки бывают упорядоченные и неупорядоченные. В упорядоченной выборке существенен порядок, в котором следуют ее элементы, другими словами, изменив порядок элементов, мы получим другую выборку. Например, из цифр 1, 2, 3, 4, 5 составляем трехзначные числа 123, 431, 524, ...и т.д. Это упорядоченные трехэлементные выборки, ведь 123 и 132 - разные числа. Другой пример: из 20 учащихся класса будем выбирать двух дежурных. Любая пара дежурных представляет собой неупорядоченную двухэлементную выборку, так как порядок их выбора не важен.

Определение. Размещениями из n элементов по m (m 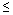n) называются упорядоченные m -элементные выборки из данных n элементов. Из определения следует, что размещения отличаются друг от друга либо самими элементами, либо их порядком.

Число размещений из n по m обозначается 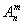Чтобы вывести формулу числа размещений, заметим, что первый элемент в выборку мы можем выбрать n способами, второй из оставшихся n-1 элементов (n-1) способами, третий - (n-2) способами и так далее, m-й элемент можно выбрать n-(m-1) = n-m+1 способами. По правилу произведения получим:

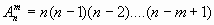(1.1)

Это и есть формула для вычисления числа размещений. Найдем, например, число размещений из 7 по 3. Здесь n = 7, n - m +1 =5. Значит,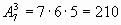

Заметим, что верхний индекс 3 показывает, сколько сомножителей надо взять в произведение. Приведем еще несколько примеров:

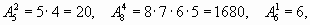
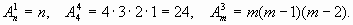
Пример 3.1. Составить все из трех букв А, В, С по две буквы.

Решение. Это будут: АВ, АС, ВС, ВА, СА, СВ. Проверим по формуле: 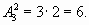Их действительно 6 штук. Отметим, что АВ и ВА - разные размещения.

Пример 3.2. На пяти карточках написаны числа 1, 2, 3, 4, 5. Сколько различных трехзначных чисел можно из них составить?

Решение. Трехзначные числа представляют собой трехэлементные выборки из пяти цифр, причем, выборки упорядоченные, поскольку порядок цифр в числе существенен. Значит, этих чисел будет столько, сколько существует из пяти элементов по 3.

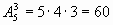
Ответ: 60 чисел.

Часто формулы комбинаторики записывают с помощью факториалов. Произведение всех последовательных натуральных чисел от 1 до n обозначается n! (читается: эн-факториал).

n! = 1 · 2 · 3 · ... · n.

Эту Формулу можно теперь преобразовать следующим образом. Умножим и разделим правую часть этой формулы на выражение

(n-m)! = 1 · 2 · 3 · ... ·(n-m).

Тогда получится:

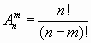(1.2)

вычислим например, 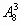по этой формуле: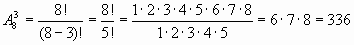
Мы видим, что здесь приходится еще сокращать дробь, поэтому для вычисления числа с конкретными значениями m и n первая формула предпочтительнее. Условились считать, что 0! =1.

Перестановки

Определение. Перестановками из n элементов называются размещения из n элементов по n. Из определения следует, что в данном случае в упорядоченную выборку входят все n элементов и отличаться выборки могут только порядком. Поэтому все перестановки имеют один и тот же состав и отличаются только порядком элементов. Число перестановок из n элементов обозначается Рn. Подставляя в формулу (1.1) или (1.2) m = n, получим формулу для вычисления числа перестановок из n элементов:

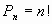(1.3)

Приведем несколько примеров использования этой формулы.

Р5 = 5! = 1· 2 ·3 · 4 ·5 = 120; Р2 = 2! = 1· 2 = 2; Р1 = 1! = 1.

Пример 4.1.Составить все размещения из трех букв А, В, С.

Решение. АВС, АСВ, ВАС, ВСА, СВА, САВ. Проверим по формуле:

Р₃ = 1·2·3 = 6.

Пример 4.2. Сколькими способами можно расставить 7 книг на книжной полке? Решение.Каждая расстановка будет отличаться от другой порядком следования книг. Поэтому это будут перестановки из семи элементов.

Р₇ = 7! = 1·2·3·4·5·6·7= 5040.

Ответ: 5040 способами.

Пример 4.3. Сколько шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5 так, чтобы цифры в числе не повторялись?

Решение. Из данных шести цифр можно составить Р₆ = 6! = 720 перестановок. Но числа, начинающиеся на нуль, не являются шестизначными. Такие числа отличаются друг от друга перестановкой пяти остальных цифр, значит, их будет Р₅ = 120. Поэтому шестизначных чисел будет 720 - 120 = 600.

Ответ: 600 чисел.

Сочетания

Определение. Сочетаниями из n элементов по m (m 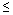n) называются неупорядоченные m-элементные выборки из данных n элементов.
Ясно, что все сочетания отличаются друг от друга хотя бы одним элементом, а порядок элементов здесь не существенен. Число сочетаний из n по m обозначается 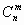Чтобы из сочетаний получить размещения, надо упорядочить каждую m-элементную выборку, а это можно сделать m! способами. Следовательно, число сочетаний 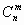меньше числа размещений 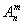в m! раз. Учитывая этот факт, из формул (1.1) и (1.2) получим соответствующие формулы для вычисления числа сочетаний:

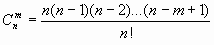(1.4) и

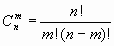(1.5)

Например,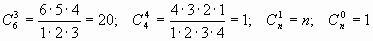

Пример 5.1. Составить все сочетания из трех букв А, В, С по две буквы.

Решение. Это будут АВ, АС, ВС. Проверим по формуле: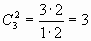

(Обратите внимание, что АВ и ВА - это одно и то же сочетание, на разные размещения.)

Пример 5.2. Из 20 учащихся надо выбрать двух дежурных. Сколькими способами это можно сделать?

Решение Надо выбрать двух человек из 20. Ясно, что от порядка выбора ничего не зависит, то есть Иванов-Петров или Петров-Иванов - это одна и та же пара дежурных. Следовательно, это будут сочетания из 20 по 2.

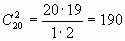
Ответ: 190 способами.

Пример 5.3. Сколькими способами можно группу из 15 учащихся разделить на две группы так, чтобы в одной группе было 4, а в другой - 11 человек?

Решение. Чтобы разделить эту группу, достаточно выбрать 4 человека из 15, а оставшиеся сами образуют другую группу. А выбрать 4 человека из 15 можно 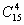способами.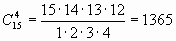

Ответ: 1365 способами.

Эту задачу можно было решить по-другому: из 15 учащихся выбрать 11 , а остальные 4 образуют другую группу. Это можно осуществить 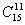cпособами.

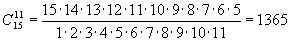
Получается тот же ответ и возникает подозрение, что

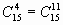. Это действительно так. Сочетания обладают свойством

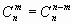(1.6)

в чем легко убедиться с помощью формулы (1.5):

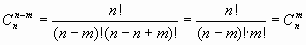
Пользуясь этой формулой, вычислим .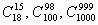

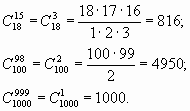
Перестановки с повторениями

До сих пор мы рассматривали комбинации, в которых элементы не повторялись, то есть каждый из них можно было взять в выборку только один раз. Если же это ограничение убрать, то получим еще три вида комбинаций: перестановки, размещения и сочетания с повторениями.
Рассмотрим, например, слово "КВАНТ", состоящее из пяти различных букв. Если менять порядок букв, получим 5! =120 перестановок, т.е. 120 новых слов. (Словом будем называть любую комбинацию букв). Если проделать то же со словом "АТАКА", то перестановок будет меньше, потому что, меняя местами первую, третью и пятую буквы, будем получать то же самое слово. И, так как три буквы "А" можно менять местами 3! = 6 способами, то и перестановок в слове "АТАКА" будет в 6 раз меньше.

А теперь рассмотрим общий случай. Пусть дана выборка

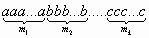
состоящая из n элементов, причем, элемент а повторяется m₁ раз, элемент b - m₂ раз, и т.д., элемент с - m_k раз и m₁ + m₂ +...+ m_k = n. Перестановки в такой выборке, где есть одинаковые элементы, называются перестановками с повторениями и число перестановок с повторениями обозначается P_n(m₁,m₂,....,m_k) Из приведенных выше рассуждений следует формула:

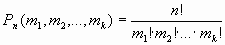(1.8)

Пример 7.1. Сколькими способами можно расставить белые фигуры (2 ладьи, 2 коня, 2 слона, ферзь и король) на первой линии шахматной доски?

Решение.Первая линия шахматной доски представляет собой 8 клеток, на которых и надо расположить эти 8 фигур. Различные варианты расположения будут отличаться только порядком фигур, значит, это будут перестановки с повторениями Р₈ (2,2,2). По формуле:

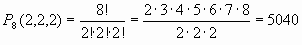
Ответ: 5040 способами

Пример 7.2. У мамы 2 яблока, 3 груши и 4 апельсина. Каждый день в течение девяти дней она выдает сыну по одному фрукту. Сколько может быть вариантов такой выдачи? Решение. Обозначая фрукты по первым буквам названия, составим несколько вариантов выдачи: ЯЯГГГАААА, ААГГЯГААЯ, ГГГААЯЯАА. Эти выборки имеют один и тот же состав и отличаются только перестановкой элементов, поэтому применяем формулу числа перестановок с повторениями.

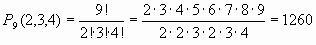
Ответ: 1260 вариантов

Размещения с повторениями

Сочетания с повторениями

Определение. Вероятностью события A (Р(А)) при проведении некоторого испытания называют отношения числа «удачных» исходов (в результате которых наступает событие А) к общему числу всех равновозможных между собой исходов этого испытания.

В течение всех лет обучения в школе мы много решаем разнообразных задач, в том числе и логических: задачи занимательного характера, головоломки, анаграммы, ребусы и т.п. Чтобы успешно решать задачи такого вида, надо уметь выделять их общие признаки, подмечать закономерности, выдвигать гипотезы, проверять их, строить цепочки рассуждений, делать выводы. Логические задачи от обычных отличаются тем, что не требуют вычислений, а решаются с помощью рассуждений. Можно сказать, что логическая задача – это особая информация, которую не только нужно обработать в соответствии с заданным условием, но и хочется это сделать. Логика помогает усваивать знания осознанно, с пониманием, т.е. не формально; создаёт возможность лучшего взаимопонимания.

Логика – это искусство рассуждать, умение делать правильные выводы. Это не всегда легко, потому что очень часто необходимая информация «замаскирована», представлена неявно, и надо уметь её извлечь. Как известно, видение рождает мышление. Возникает проблема: как установить логические связи между разрозненными фактами и как оформить в виде единой целой. Видеть ход доказательства и решения задач позволяет метод граф - схем, который делает доказательство более наглядным и позволяет кратко и точно изложить доказательства теорем и решения задач.

Метод граф

Слово «граф» в математической литературе появилось совсем недавно. Понятие графа используется не только в математике, но и в технике и даже в повседневной жизни под разными названиями – схема, диаграмма.

Особенно большую помощь графы оказывают при решении логических задач. Представляя изучаемые объекты в наглядной форме, «графы» помогают держать в памяти многочисленные факты, содержащиеся в условии задачи, устанавливать связь между ними.

Графом называется любое множество точек, некоторые из которых соединены линиями или стрелками. Точки, изображающие элементы множества, называют вершинами графа, соединяющие их отрезки – рёбрами графа. Точки пересечения рёбер графа не являются его вершинами. Во избежание путаницы вершины графа часто изображают не точками, а маленькими кружочками. Рёбра иногда удобнее изображать не прямолинейными отрезками, а дугами.

Родившись при решении головоломок и занимательных игр ( задачи о шахматном коне, о ферзях, « кругосветное путешествие », задачи о свадьбах и гаремах и т.п. ), теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем.

Пример 1.1.Красный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша отличается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?

Решение.Обозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке, а пунктирная, что не лежит. Тогда с учетом задачи имеем G1 (рис. 1).

Рис.1

Далее достраиваем граф по следующему правилу: поскольку в короб может лежать ровно один карандаш, то из каждой точки должны выходить одна сплошная линия и три пунктирные. Получается граф G2 , дающий решение задачи.

Пример 1.2.Беседуют трое друзей: Белокуров, Чернов и Рыжов. Брюнет сказал Белокурову: «Любопытно, что один из нас белокурый, другой брюнет, третий рыжий, но ни у кого цвет волос не соответствует фамилии». Какой цвет волос имеет каждый из друзей?

Решение.Построим граф отношения, заданного в условии задачи. Для этого, прежде всего, выделим множество фамилий М и множество цветов волос К, элементы которых будем обозначать точками. Точки множества М назовем буквами Б, Ч, Р (Белокуров, Чернов и Рыжов); точки второго множества – б, бр, р (белокурый, брюнет, рыжий). Если точке из одного множества соответствует точка из другого, мы их соединим сплошной линией, а если не соответствует – штриховой. Условие задачи указывает лишь на несоответствия, поэтому вначале должен возникнуть граф, изображенный на рисунке 2.

Рис.2

Из условия задачи следует, что для каждой точки из множества М существует одна и только одна точка из множеств К, которая соответствует первой и, наоборот, каждой точке из множества К соответствует одна и только одна точка из множества М. Задача сводится к тому, чтобы найти это единственно возможное соответствие между элементами множеств М и К, т. е. к нахождению трех сплошных линий, соединяющих соответствующие точки множеств.

Принцип решения задачи прост. Если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с его третьей точкой ее необходимо соединить сплошной линией. Поэтому граф на рисунке 2 дополняется сплошными линиями, соединяющими точки Б и р, Р и бр (рис. 3).

Рис.3

Далее остается соединить сплошной линией точку Ч и точку б, так как точка Ч соединена с точкой бр штриховой линией, а точка р уже «занята» (рис. 4).

Рис. 4

Таким образом, на графе этого рисунка автоматически прочитываем ответ: Белокуров — рыжий, Чернов — белокурый, Рыжов – брюнет.

В следующей задаче применение графов помогает обнаружить наличие двух решений.

Пример 1.3.Маша, Лида, Женя и Катя умеют играть на разных инструментах (виолончели, рояле, гитаре и скрипке), но каждая только на одном. Они же владеют разными иностранными языками (английским, французским, немецким и испанским), но каждая только одним. Известно, что:

1. девушка, которая играет на гитаре, говорит по-испански;

2. Лида не играет ни на скрипке, ни на виолончели и не знает английского языка;

3. Маша не играет ни на скрипке, ни на виолончели и не знает английского языка;

4. девушка, которая говорит по-немецки, не играет на виолончели;

5. Женя знает французский язык, но не играет на скрипке.

Кто на каком инструменте играет и какой иностранный язык знает?

Решение. Условию задачи соответствует граф, изображенный на рисунке 5.

Рис. 5

Проведем последовательно следующие сплошные отрезки: КС, ВЖ, ВФ, АК (рис.6).

Рис. 6

Тем самым образуются два «сплошных» треугольника ЖВФ и КСА. Проводим еще сплошной отрезок РН. Теперь убеждаемся, что условия задачи не обеспечивают однозначности выбора третьей точки для каждой из пар РН и ГИ. Возможны следующие варианты «сплошных» треугольников: МГИ и ЛРН или ЛГИ и МРН. Таким образом, задача имеет два решения.

Метод кругов Эйлера

Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.

Один из величайших математиков петербургский академик Леонард Эйлер за свою долгую жизнь (он родился в 1707 г., а умер в 1783 г.) написал более 850 научных работ. В одной из них и появились эти круги. Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры.

Пример 1.4.Часть жителей города умеет говорить только по-русски, часть – только по-узбекски и часть умеет говорить на обоих языках. По-узбекски говорят 85%, по-русски 75%. Сколько процентов жителей говорят на обоих языках?

Решение.Составим схему.

В кружке под буквой «У» обозначим жителей, говорящих по-узбекски, под буквой «Р» - по-русски. В общей части кружков обозначим жителей, говорящих на обоих языках. Теперь от всех жителей (100%) отнимем кружок «У» (85%), получим жителей, говорящих только по-русски (15%). А теперь от всех, говорящих по-русски (75%), отнимем эти 15%. Получим говорящих на обоих языках (60%).

Общие правила комбинаторики

Решение многих комбинаторных задач основывается на двух фундаментальных правилах, называемых правилом суммы и правилом произведения. Прежде всего определимся в терминологии. Если имеется, к примеру, 5 шаров в ящике, то мы будем говорить, что один шар из ящика можно выбрать пятью способами.

Правило суммы. Если объект А можно выбрать n способами, а объект В-k способами, то объект "А или В" можно выбрать n+k способами.

Пример 2.1.В ящике находятся 20 шаров: 5 белых, 6 черных, 7 синих и 2 красных. Сколькими способами можно взять из ящика один цветной шар?

Решение.Здесь предполагается, что цветной шар - это синий или красный, поэтому надо применять правило суммы. Цветной шар можно выбрать 7 + 2 = 9 способами.

Правило произведения. Если объект А можно выбрать n способами, а объект В независимо от него - k способами, то пару объектов "А и В" можно выбрать n·k способами.

Пример 2.2.Сколько может быть различных комбинаций выпавших граней при бросании двух игральных костей? (Игральная кость - это кубик, на гранях которого нанесены числа 1, 2, 3, 4, 5, 6 )
Решение. На первой кости может выпасть 1, 2, 3, 4, 5 или 6 очков, то есть всего будет 6 вариантов. Точно так же и на второй кости 6 вариантов. По получится всего 6 · 6 = 36 способов. Правила суммы и произведения справедливы не только для двух, но и для любого числа объектов. Приведем еще несколько примеров, в которых необходимо выбрать правило суммы или произведения.

Пример 2.3.Из города А в город В ведут 5 дорог, а из города В в город С - 3 дороги. Сколькими способами можно проехать из города А в город С?
Решение. Чтобы проехать из А в С, надо проехать из А в В и из В в С, поэтому применим правило произведения. 5 · 3 = 15.

Пример 2.4. На книжной полке стоят 3 книги по алгебре, 4 книги по геометрии и 5 книг по литературе. Сколькими способами можно взять с полки одну книгу по математике?
Решение.Книга по математике - это книга по алгебре или по геометрии. Применяем правило суммы. 3 + 4 = 7.

Пример 2.5.В меню имеется 4 первых блюда, 3 вторых и 2 третьих. Сколько различных полных обедов можно из них составить?
Решение.Полный обед состоит из первого, и второго, и третьего блюд. По правилу произведения получаем 4 · 3 · 2 = 24 различных полных обеда.

Размещения

Если из данного множества предметов мы будем выбирать некоторое подмножество, то его будем называть выборкой. Выборки бывают упорядоченные и неупорядоченные. В упорядоченной выборке существенен порядок, в котором следуют ее элементы, другими словами, изменив порядок элементов, мы получим другую выборку. Например, из цифр 1, 2, 3, 4, 5 составляем трехзначные числа 123, 431, 524, ...и т.д. Это упорядоченные трехэлементные выборки, ведь 123 и 132 - разные числа. Другой пример: из 20 учащихся класса будем выбирать двух дежурных. Любая пара дежурных представляет собой неупорядоченную двухэлементную выборку, так как порядок их выбора не важен.

Определение. Размещениями из n элементов по m (m 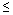n) называются упорядоченные m -элементные выборки из данных n элементов. Из определения следует, что размещения отличаются друг от друга либо самими элементами, либо их порядком.

Число размещений из n по m обозначается 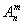Чтобы вывести формулу числа размещений, заметим, что первый элемент в выборку мы можем выбрать n способами, второй из оставшихся n-1 элементов (n-1) способами, третий - (n-2) способами и так далее, m-й элемент можно выбрать n-(m-1) = n-m+1 способами. По правилу произведения получим:

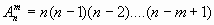(1.1)

Это и есть формула для вычисления числа размещений. Найдем, например, число размещений из 7 по 3. Здесь n = 7, n - m +1 =5. Значит,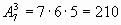

Заметим, что верхний индекс 3 показывает, сколько сомножителей надо взять в произведение. Приведем еще несколько примеров:

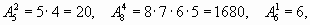
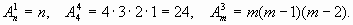
Пример 3.1. Составить все из трех букв А, В, С по две буквы.

Решение. Это будут: АВ, АС, ВС, ВА, СА, СВ. Проверим по формуле: 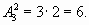Их действительно 6 штук. Отметим, что АВ и ВА - разные размещения.

Пример 3.2. На пяти карточках написаны числа 1, 2, 3, 4, 5. Сколько различных трехзначных чисел можно из них составить?

Решение. Трехзначные числа представляют собой трехэлементные выборки из пяти цифр, причем, выборки упорядоченные, поскольку порядок цифр в числе существенен. Значит, этих чисел будет столько, сколько существует из пяти элементов по 3.

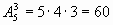
Ответ: 60 чисел.

Часто формулы комбинаторики записывают с помощью факториалов. Произведение всех последовательных натуральных чисел от 1 до n обозначается n! (читается: эн-факториал).

n! = 1 · 2 · 3 · ... · n.

Эту Формулу можно теперь преобразовать следующим образом. Умножим и разделим правую часть этой формулы на выражение

(n-m)! = 1 · 2 · 3 · ... ·(n-m).

Тогда получится:

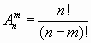(1.2)

вычислим например, 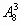по этой формуле: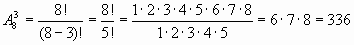
Мы видим, что здесь приходится еще сокращать дробь, поэтому для вычисления числа с конкретными значениями m и n первая формула предпочтительнее. Условились считать, что 0! =1.

Перестановки

Определение. Перестановками из n элементов называются размещения из n элементов по n. Из определения следует, что в данном случае в упорядоченную выборку входят все n элементов и отличаться выборки могут только порядком. Поэтому все перестановки имеют один и тот же состав и отличаются только порядком элементов. Число перестановок из n элементов обозначается Рn. Подставляя в формулу (1.1) или (1.2) m = n, получим формулу для вычисления числа перестановок из n элементов:

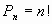(1.3)

Приведем несколько примеров использования этой формулы.

Р5 = 5! = 1· 2 ·3 · 4 ·5 = 120; Р2 = 2! = 1· 2 = 2; Р1 = 1! = 1.

Пример 4.1.Составить все размещения из трех букв А, В, С.

Решение. АВС, АСВ, ВАС, ВСА, СВА, САВ. Проверим по формуле:

Р₃ = 1·2·3 = 6.

Пример 4.2. Сколькими способами можно расставить 7 книг на книжной полке? Решение.Каждая расстановка будет отличаться от другой порядком следования книг. Поэтому это будут перестановки из семи элементов.

Р₇ = 7! = 1·2·3·4·5·6·7= 5040.

Ответ: 5040 способами.

Пример 4.3. Сколько шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5 так, чтобы цифры в числе не повторялись?

Решение. Из данных шести цифр можно составить Р₆ = 6! = 720 перестановок. Но числа, начинающиеся на нуль, не являются шестизначными. Такие числ