Тема 8. Непараметрические методы математической статистики
Основные понятия по теме:
1. Неравенство Чебышева, теорема Чебышева.
2. Объединение, пересечение нечетких множеств, дополнение нечетких множеств.
3. Статистическая, нулевая, простая, сложная гипотезы.
4. Ошибки первого и второго рода.
5. Статистический критерий.
6. Уровень значимости.
7. Проверка гипотез.
8. Основные понятия дисперсионного анализа.
9. Общая, факторная, остаточная, исправленная факторная дисперсии.
Применение этих понятий на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. Критическая область для проверки гипотезы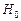 
имеет вид: 
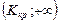. Гипотеза будет принята, если …
1) * 
;
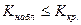2) 
;
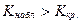3) 
;
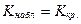4) 
;
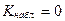5) 
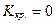
2. Критическая область для проверки гипотезы 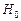имеет вид: 
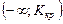. Гипотеза будет принята, если …
1) 
;
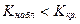2)* 
;
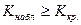3) ;
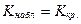4) ;
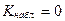5)
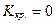
3. Критическая область для проверки гипотезы 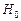имеет вид: 
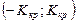. Гипотеза 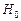будет принята, если …
1) ;
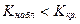2)* 
;
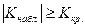3) ;
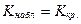4) 
;
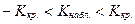5)
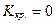
4. Предполагается, что выборки извлечены из нормальных совокупностей с одинаковыми дисперсиями. Проверить нулевую гипотезу о равенстве групповых средних, если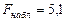 
, 
.
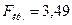1) верна;
2) * не верна;
3) другой ответ
5. Проведены измерения признака на трех уровнях при четырех испытаниях на каждом из них.
Общая дисперсия признака равна 286, факторная дисперсия 150. Найти остаточную дисперсию.
1)* 136;
2) 163;
3) 124;
4) 150;
5) 104
6. Проведены измерения признака на трех уровнях при четырех испытаниях на каждом из них.
Общая дисперсия равна 286, факторная дисперсия 150. Найти исправленную факторную дисперсию.
1) 286-150;
2)* 
;
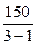3) 
;
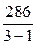4) 
;
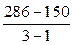5) 
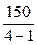
7. Проведены измерения признака на трех уровнях при четырех испытаниях на каждом из них.
Общая дисперсия равна 286, факторная дисперсия 150. Найти остаточную исправленную дисперсию.
1)* 
;
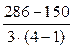2) ;
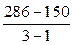3) 
;
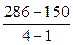4) 
;
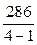5)
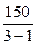
Тема 9. Основы математической статистики
Для успешной сдачи тестов студент должен знатьследующие определения математической статистики:
1. Генеральная и выборочная совокупности.
2. Вариационный ряд и его характеристики.
3. Точечные оценки, их свойства. Интервальные оценки.
4. Метод произведений.
Применение этих понятий на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. Вариантой с наибольшей частотой вариационного ряда является …
 |  | |||
 |
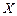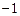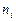1) 1;
2) 
;
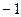3) 0;
4)*6;
5)27
2. Объем выборки, представленной вариационным рядом равен …
| | | ||
| |
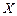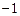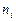1) 15;
2) 20;
3)* 45;
4) 2;
5) 30
3. Вариационный ряд:
| |  |  |  |
| |
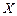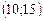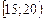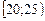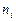Является вариационным рядом …
1) с равностоящими вариантами;
2) с неравностоящими вариантами;
3)* интервальным;
4) неинтервальным;
5) другой ответ
4. Для вариационного ряда выборочное среднее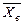 
, выборочная дисперсия 
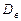равны …
| | | ||
| |
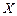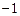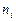5. Доверительный интервал для оценки математического ожидания при выборочной средней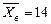 
и точности оценки 
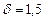имеет вид …
1)* -0,2; 0,76,
2) 0;1 ,
3) 0;0,8.
Тема 10. Корреляция
Основные понятия по теме теории корреляции
Применение этих понятий на практических примерах.
Примерные тестовые задания, предлагаемые в этой теме:
1. В формуле для вычисления коэффициента линейной корреляции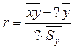 
вместо «?» надо поставить …
1)* 
; 
;
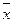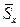2) 
; 
;
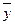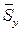3) , 
;
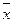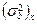4) 1,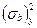 
;
5) 0,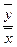 
.
2. Пусть в результате измерения величины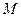 
получено значение 
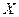, и пусть на процесс измерения влияет случайный независимый фактор 
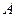. Тогда для оценки значимости фактора 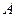применяют …
1) *однофакторный дисперсионный анализ;
2)*двухфакторный дисперсионный анализ;
3) корреляционный анализ;
4) регрессионный анализ;
5) трехфакторный дисперсионный анализ
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА ДЛЯ ПОДГОТОВКИ К ТЕСТИРОВАНИЮ И ЭКЗАМЕНУ (ЗАЧЕТУ)
Учебники
1. Булдык, Г. М. Теория вероятностей и математическая статистика: учеб. пособие для экон. спец. вузов / Г. М. Булдык. — Мн.: Выш. шк., 1989. — 284 с.
2. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие для студ. вузов / В. Е. Гмурман. — М.: Высш. шк., 1998. — 480 с.
3. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В. Е. Гмурман. — М.: Высш. шк., 2003. — 479 с.
4. Жевняк, Р. М. Теория вероятностей и математическая статистика: учеб. пособие для вузов / Р. М. Жевняк, А. А. Карпук, В. Т. Унукович. — Мн.: Харвест, 2000. — 384 с.
5. Колемаев, В. А. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В. А. Колемаев, О. В. Староверов, В. Б. Турундаевский; под ред. В. А. Колемаева. — М.: Высш. шк., 1991. — 400 с.
Задачники
6. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для студ. вузов / В. Е. Гмурман. — М.: Высш. шк., 1998. — 400 с.
7. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / В. Е. Гмурман. — М.: Высш. шк., 2003. — 405 с.