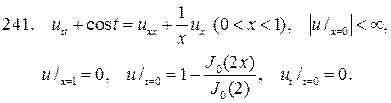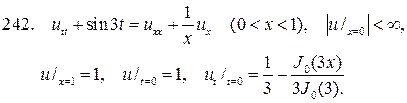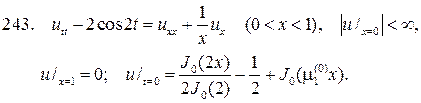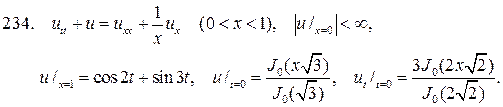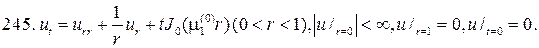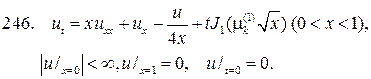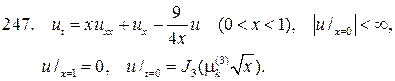Следовательно, решение смешанной задачи нужно искать в виде суммы

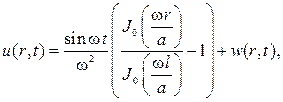
и функция w(x,t) , будет уже решением однородной смешанной задачи

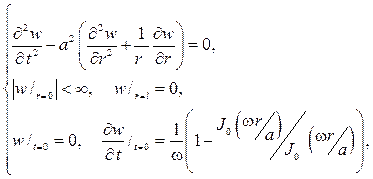
которая решается в соответствии с простейшей схемой метода Фурье.

Как и при решении задачи 229 придем к ряду

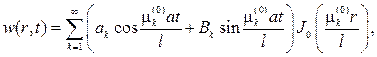
где 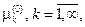положительные нули цилиндрической функции J₀(x). Что касается коэффициентов А_k, то из начального условия w/_t=0=0 будет следовать

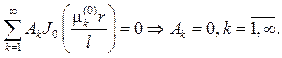
Второе начальное условие приведет к равенству

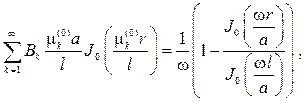
откуда в силу ортогональности собственных функций с весом r на[0,l] найдем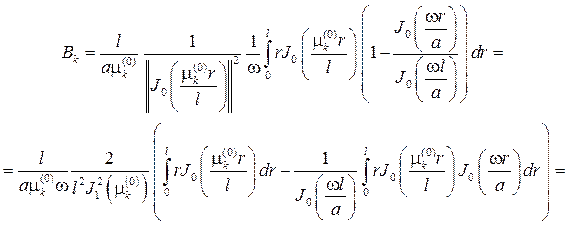

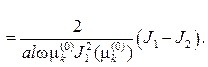
Чтобы вычислить J₁ , нужно сделать замену переменной интегриро- вания и воспользоваться равенством (73), соответственно получим

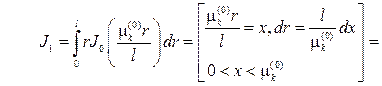
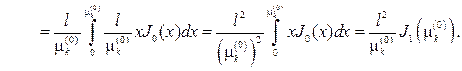
Чтобы вычислить

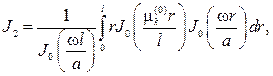
заметим, что

,

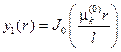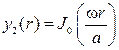
удовлетворяют уравнениям

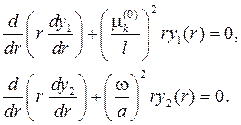
Умножив первое из этих уравнений на y₂( r ), второе на y₁( r), вычитая полученные результаты и интегрируя в пределах от 0 до l, будем иметь

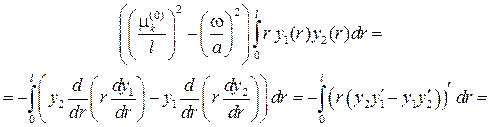
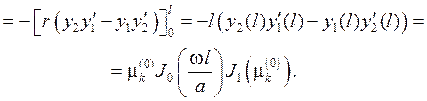
Возвращаясь теперь к J₂ , получим

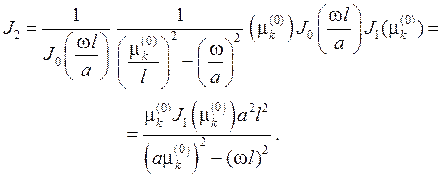
Подставляя теперь найденные значения J₁ и J₂в выражение для В_k , найдем

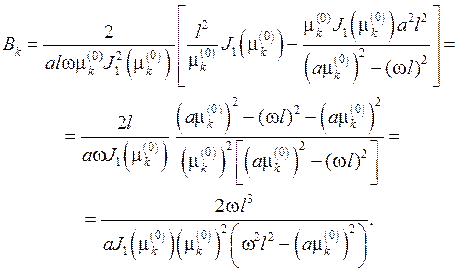
В итоге придем к ответу

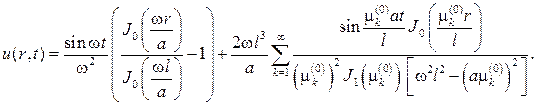
Заметим в заключение, что рассматривается так называемый нерезо- нансный случай, когда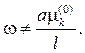

233. Найти радиальное распределение температуры в бесконечном круго- вом цилиндре радиуса l , боковая поверхность которого поддерживается при постоянной температуре u₀ . Начальная температура внутри цилиндра равна нулю.

Р е ш е н ие. После перевода текста на формулы придем к смешанной задаче

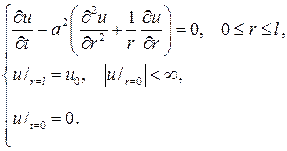
С помощью замены

u(r,t)=u₀+v(r,t)

получим смешанную задачу для функции v(r,t):

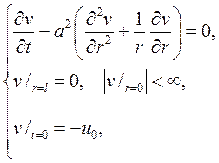
решение которой уже ищем в виде произведения R(r)и T(t) так, что

v(r,t)=R(r)T(t).

Разделив переменные, придем к двум обыкновенным дифферен- циальным уравнениям:

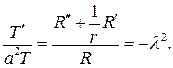
С учетом граничных условий относительно радиальной функции R(r) придем к задаче Штурма Лиувилля

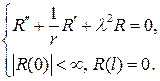
Такая задача уже встречалась ранее в задачах 229 и 230, ее собствен- ные значения и собственные функции будут

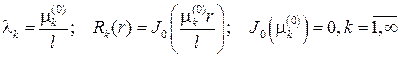
Собственные функции ортогональны между собой с весом р(r)=r. Дифференциальное решение для функции T(t) имеет вид

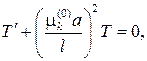
его можно решить как линейное с постоянным коэффициентом и мето- дом разделения переменных, тогда получим

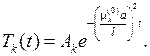
Перемножая T_k(t) на собственные функции и суммируя, придем к ряду

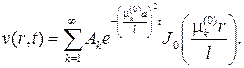
Подставляя этот ряд в начальное условие, будем иметь

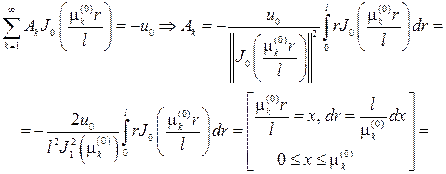
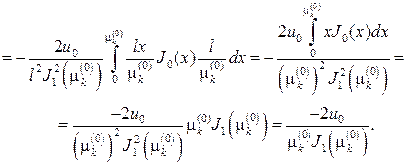
Итак решение исходной задачи будет выражаться рядом

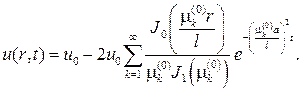
234. Дан неограниченный цилиндр радиуса l , на поверхности которого поддерживается постоянная концентрация u₀ вещества. Определить коли- чество вещества, продиффундировавшего внутрь цилиндра в момент вре- мени t, на единицу длины, если начальная концентрация u(r,t)/_t=0=0.

Р е ш е н и е. Поскольку уравнение теплопроводность есть одновре -

менно и уравнение диффузии, то будем иметь смешанную задачу

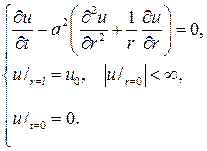
Эта задача идентична встретившейся задаче 233 , поэтому ее решение сразу выписываем:

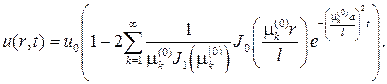
Теперь мы должны взять интеграл от концентрации, т. е.

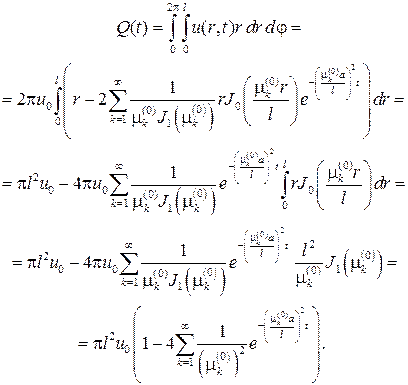
235. Дана неограниченная цилиндрическая труба 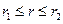, и ее началь- ная температура u(r,0)=f(r). Внутренняя и наружная поверхности трубы поддерживаются при нулевой температуре. Найти распределение температуры в сечении u(r,t) при t>0.

Р е ш е н и е. Здесь возникает смешанная задача

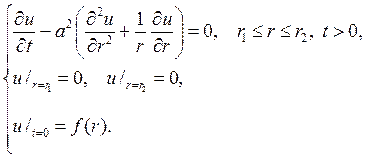
Полагая u(r,t)=R(r)T(t), после разделения переменных придем к соот- ношениям

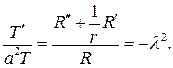
С учетом граничных условий для радиальной функции получим зада- чу Штурма Лиувилля

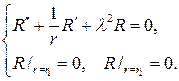
Собственные функции будут ортогональными на отрезке [r₁ ,r₂] с весом r.

Общее решение дифференциального уравнения будет иметь вид

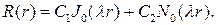
Подставив его в граничные условия, придем к соотношениям

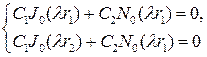
для определения С₁, С₂ и λ .Однородная система линейных уравнений имеет нетривиальные решения, если ее определитель

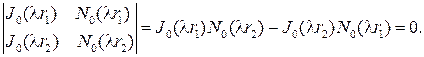
Корни 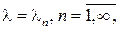уравнения

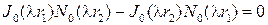
и будут собственными значениями, а собственные функции, как нетрудно проверить, будут иметь вид

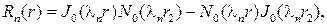
как уже отмечалось, они образуют ортогональную систему с весом r на отрезке 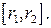Найдем квадрат нормы

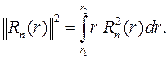
Через y_n(r) обозначим функцию

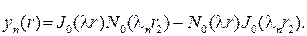
Радиальная собственная функция R_n(r) и y_n(r) суть соответственно решения уравнений

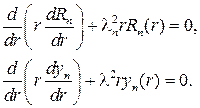
Умножим первое уравнение на y_n(r),второе – на R_n(r), вычтем из пер- вого второе и проинтегрируем по отрезку [r_1, r₂.]. В итоге получим

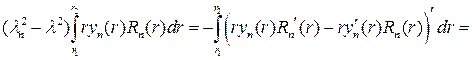
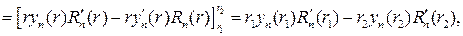
откуда следует, что

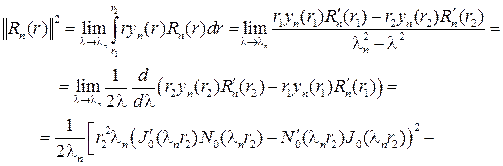
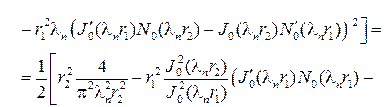
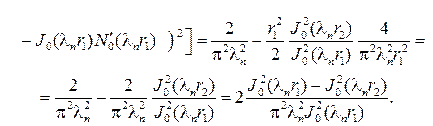
Здесь использованы соотношения, вытекающие из определения соб-

ственных значений и формулы для определителя Вронского

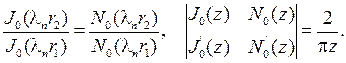
Из дифференциального уравнения для временной функции

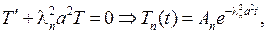
поэтому умножая T_n(t) на собственную функцию, найдем ряд

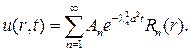
Подставляя этот ряд в начальное условие, будем иметь

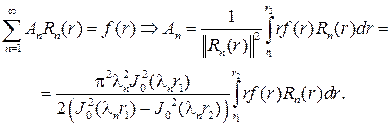
Ответ запишется в форме

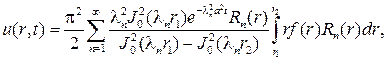
где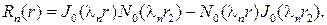

236. Найдите распределение температуры внутри бесконечного круглого цилиндра радиуса l , если начальная температура 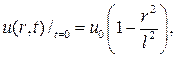и на поверхности цилиндра поддерживается нуле- вая температура.

237. Решите задачу о свободных колебаниях однородной круглой мемб- раны радиуса l, закрепленной по краю, если начальные скорости ее точек равны нулю, а начальное отклонение

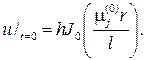
Здесь 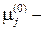положительный корень уравнения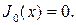

Решите следующие смешанные задачи