Основные теоремы о пределах функций
Теорема 2.4.1. Функция у = f(х) не может иметь более одного предела при х ® а.
Доказательство. Предположим противное, пусть функция у = f(х) при х ® а имеет два предела b1 и b2:  f(х) = b1,
f(х) = b1,  f(х) = b2, причём b1 ¹ b2.
f(х) = b2, причём b1 ¹ b2.
Согласно теореме 2.2.1 из этих равенств следует, что у = b1 + о1(х), у = b2 + о2(х). Поэтому b1 – b2 = о2(х) – о1(х). Последнее равенство невозможно, так как в левой части стоит постоянная, отличная от нуля, а в правой – бесконечно малая функция. Пришли к противоречию. Теорема
доказана.
Теорема 2.4.2. Если каждая из функций у(х) и z(х) имеет предел
при х ® а, то сумма, разность и произведение этих функций также имеют пределы, причём
 ( у(х) ± z(х)) =
( у(х) ± z(х)) =  у(х) ±
у(х) ±  z(х), (3)
z(х), (3)
 ( у(х) ×z(х)) =
( у(х) ×z(х)) =  у(х) ×
у(х) ×  z(х). (4)
z(х). (4)
Если, кроме того,  z(х) ¹ 0, то и частное
z(х) ¹ 0, то и частное 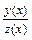 имеет предел, причём
имеет предел, причём

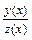 =
= 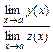 . (5)
. (5)
Доказательство. Пусть  у(х) = b,
у(х) = b,  z(х) = с, тогда на основании теоремы 2.2.1 у(х) = b + о1(х), z(х) = с + о2(х). Тогда получаем у(х) ± z(х) = (b ± с) + (о1(х) ± о2(х)), где b ± с – постоянная, а о1(х) ± о2(х) – бесконечно малая при х ® а.
z(х) = с, тогда на основании теоремы 2.2.1 у(х) = b + о1(х), z(х) = с + о2(х). Тогда получаем у(х) ± z(х) = (b ± с) + (о1(х) ± о2(х)), где b ± с – постоянная, а о1(х) ± о2(х) – бесконечно малая при х ® а.
Согласно теореме 2.2.1 из последнего равенства следует, что
 ( у(х) ± z(х)) = b ± с =
( у(х) ± z(х)) = b ± с =  у(х) ±
у(х) ±  z(х).
z(х).
Поскольку
у(х)×z(х) = (b + о1(х))(с + о2(х)) = bc + (b×о2(х) + c×о1(х) + о1(х)×о2(х)),
где bc – постоянная, о3(х) = b×о2(х) + c×о1(х) + о1(х)×о2(х) – бесконечно малая при х ® а, то на основании теоремы 2.2.1 получаем
 ( у(х) ×z(х)) = bc =
( у(х) ×z(х)) = bc =  у(х) ×
у(х) ×  z(х).
z(х).
Предположив, что  z(х) = с ¹ 0, составим разность
z(х) = с ¹ 0, составим разность
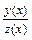 –
– 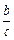 =
= 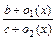 –
– 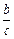 =
= 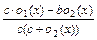 .
.
Обозначив v(x) = 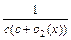 , о3(х) = c×о1(х) – b×о2(х), получим
, о3(х) = c×о1(х) – b×о2(х), получим
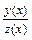 –
– 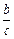 = v(x)× о3(х),
= v(x)× о3(х),  (v(x)× о3(х)) = 0,
(v(x)× о3(х)) = 0,
так как v(x) – ограниченная функция, а о3(х) – бесконечно малая функ-
ция при х ® а. Следовательно,

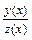 =
= 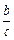 =
= 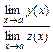 .
.
Теорема доказана.
Следствие 1. Постоянный множитель можно выносить за знак предела:
 (с×у(х)) = с×
(с×у(х)) = с×  у(х).
у(х).
Следствие 2. Если  у(х) = b и m – натуральное число, то
у(х) = b и m – натуральное число, то
 (у(х)m) = (
(у(х)m) = (  у(х))m,
у(х))m,
в частности,
 (хm) = (
(хm) = (  х)m = am.
х)m = am.
Теорема 2.4.3. Пусть три функции u = u(x), y = y(x), v = v(x) определены в некотором промежутке, содержащим точку а. Если для любого х из этого промежутка выполняются неравенства u(x) £ y(x) £ v(x) и функции u = u(x), v = v(x) имеют одинаковые пределы при х ® а, то функция y = y(x) имеет тот же предел при х ® а.
Теорема 2.4.4. Пусть функция у = f(х) определена в некотором промежутке, содержащим точку а. Если при х ® а функция у = f(х) имеет положительный (отрицательный) предел, то найдётся d-окрестность точки а такая, что для всех х из этой окрестности функция положительна (отрицательна).
Теорема 2.4.5. Если функции u(x) и v(x) определены в некоторой d-окрестности точки а, для всех х из этой окрестности, х ¹ а, выполняется неравенство u(x) < v(x) и функции имеют пределы при х ® а, то  u(x) £
u(x) £  v(x).
v(x).
Доказательство. Пусть  u(x) = b,
u(x) = b,  v(x) = c. Требуется доказать, что b £ c. Предположим противное, то есть b > c.
v(x) = c. Требуется доказать, что b £ c. Предположим противное, то есть b > c.
В силу условия и теоремы 2.4.2 функция v(x) – u(x) имеет предел  (v(x) – u(x)) = c – b, c – b < 0, ибо b > c.
(v(x) – u(x)) = c – b, c – b < 0, ибо b > c.
На основании теоремы 2.4.4 найдётся d-окрестность точки а, для всех точек которой (х ¹ а) v(x) – u(x) < 0, или v(x) < u(x), что противоречит условию. Следовательно, b £ c, то есть  u(x) £
u(x) £  v(x). Теорема доказана.
v(x). Теорема доказана.
Два замечательных предела
1) 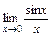 = 1; 2)
= 1; 2) 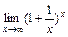 = e.
= e.
Вопросы для самоконтроля
1. Дайте определение предела функции
2. В чем заключается геометрический смысл предела функции?
3. Как определяются односторонние пределы?
4. Как связаны односторонние пределы с пределом функции? Интерпретируйте ваши рассуждения рисунками.
5. Сформулируйте определение предела функции, когда х ® ¥.
6. Какие функции называются бесконечно малыми? Приведите примеры.
7. Какие свойства бесконечно малых функций вы знаете?
8. Дайте определение бесконечно больших функций. Приведите примеры.
9. Сколько пределов может иметь функция? Докажите Ваши утверждение.
10. Сформулируйте и докажите теорему о сумме (разности), произведении и частном двух функций
11. Какие следствия можно получить из выше названной теоремы?
12. Сформулируйте и докажите теорему о сохранении знака неравенства при предельном переходе.
13. Напишите два замечательных предела.
Практическое занятие №1
Тема: Нахождение пределов
1. Найти пределы функций:
1) 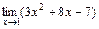 ; 2)
; 2) 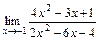 ; 3)
; 3) 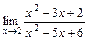 ;
;
4) 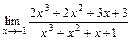 ; 5)
; 5) 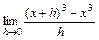 ; 6)
; 6) 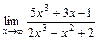 .
.
7) 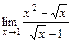 ; 8)
; 8) 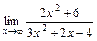 ; 9)
; 9) 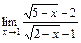 ;
;
10) 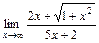 ; 11)
; 11) 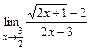 ;12)
;12) 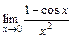 ;
;
13) 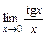 ; 14)
; 14) 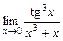 ; 15)
; 15) 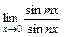 ; 16)
; 16) 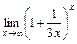 ;
;
17) 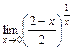 .
.
Задание для самостоятельной работы
Найти следующие пределы:
1) 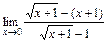 ; 2)
; 2) 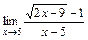 ; 3)
; 3) 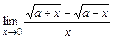 ;
;
4) 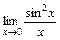 ; 5)
; 5) 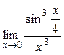 ; 6)
; 6) 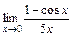 ; 7)
; 7) 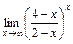 ;
;
8) 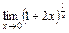 .
.
