Краткие теоретические сведения. Уравнения прямой на плоскости:
Уравнения прямой на плоскости:
y = kx + b – уравнение прямой с угловым коэффициентом,
Ax + By + D = 0 – общее уравнение прямой,
y - y 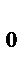 = k(x - x
= k(x - x 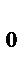 ) – уравнение прямой, проходящей через данную точку в данном направлении,
) – уравнение прямой, проходящей через данную точку в данном направлении,
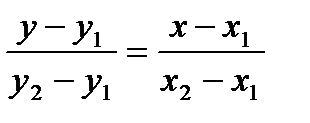 – уравнение прямой, проходящей через две точки,
– уравнение прямой, проходящей через две точки,
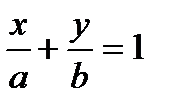 – уравнение прямой в отрезках,
– уравнение прямой в отрезках,
A(x - x 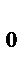 ) + B(y - y
) + B(y - y 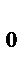 ) = 0 – уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
) = 0 – уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Вектор 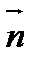 = (A, B), перпендикулярный прямой, называется нормальным вектором этой прямой.
= (A, B), перпендикулярный прямой, называется нормальным вектором этой прямой.
Условие перпендикулярности двух прямых: 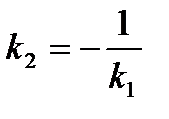 .
.
Условие параллельности двух прямых: 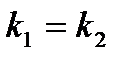 .
.
Расстояние d от точки M 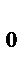 (x
(x 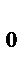 , y
, y 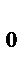 ) до прямой, заданной уравнением Ax + By + C= 0 находится по формуле: d =
) до прямой, заданной уравнением Ax + By + C= 0 находится по формуле: d = 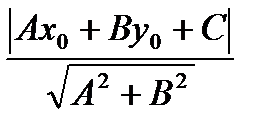 .
.
Окружностью называется множество точек плоскости, находящим на одном и том же расстоянии от некоторой точки этой же плоскости.
Каноническое уравнение окружности: (x - x 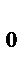 )
)  + (y - y
+ (y - y  )
) 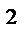 = R
= R 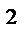 . M
. M 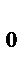 (x
(x 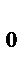 , y
, y 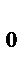 ) – центр окружности, R – радиус окружности.
) – центр окружности, R – радиус окружности.
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой же плоскости, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Каноническое уравнение эллипса: 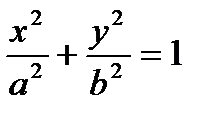 .
.
Эксцентриситетом эллипса 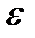 называется отношение расстояния между фокусами к большой оси. Если a > b, то
называется отношение расстояния между фокусами к большой оси. Если a > b, то 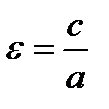 (фокусы лежат на оси абсцисс, их координаты
(фокусы лежат на оси абсцисс, их координаты 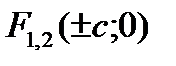 ,
, 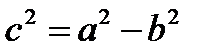 ); если b > a, то
); если b > a, то 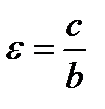 (фокусы лежат на оси ординат, их координаты
(фокусы лежат на оси ординат, их координаты 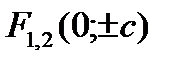 ,
, 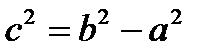 ).
).
Гиперболойназывается множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояния между фокусами.
Канонические уравнения гиперболы: 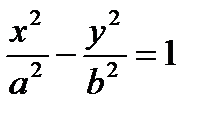 (фокусы гиперболы лежат на оси абсцисс, их координаты
(фокусы гиперболы лежат на оси абсцисс, их координаты 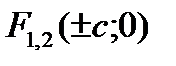 ,
, 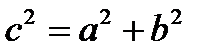 ) и
) и 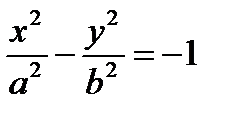 (фокусы гиперболы лежат на оси ординат, их координаты
(фокусы гиперболы лежат на оси ординат, их координаты 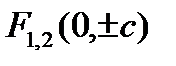 ,
, 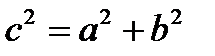 ).
).
Эксцентриситетом гиперболы 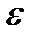 называется отношение расстояния между фокусами к действительной оси. Если фокусы гиперболы лежат на оси абсцисс, то
называется отношение расстояния между фокусами к действительной оси. Если фокусы гиперболы лежат на оси абсцисс, то 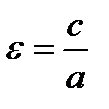 ; если фокусы гиперболы лежат на оси ординат то
; если фокусы гиперболы лежат на оси ординат то 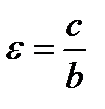 .
.
Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
Расстояние от фокуса F до директрисы параболы называется параметром параболы, обозначается p, p > 0.
Канонические уравнения параболы:
y2 = 2px (фокус имеет координаты 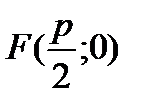 );
);
y2 = -2px (фокус имеет координаты 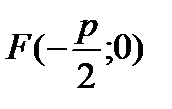 );
);
x2 = 2py (фокус имеет координаты 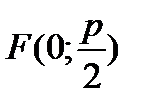 );
);
x2 = -2py (фокус имеет координаты 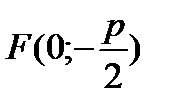 ).
).
Уравнения плоскости в пространстве:
A(x – x 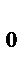 ) + B(y – y
) + B(y – y 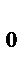 ) + C(z –z
) + C(z –z 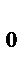 )= 0 – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору,
)= 0 – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору,
Ax+ By + Cz + D = 0 – общее уравнение плоскости,
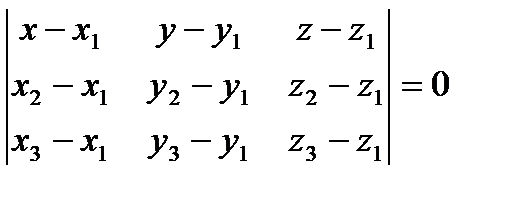 – уравнение плоскости, проходящей через три данные точки,
– уравнение плоскости, проходящей через три данные точки,
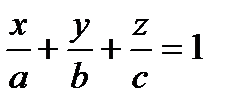 – уравнение плоскости в отрезках.
– уравнение плоскости в отрезках.
Уравнения прямой в пространстве:
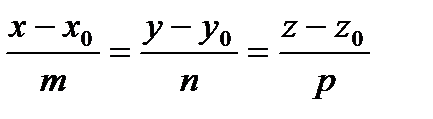 - канонические уравнения прямой,
- канонические уравнения прямой,
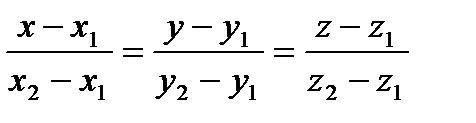 - уравнение прямой, проходящей через две точки,
- уравнение прямой, проходящей через две точки,
A 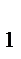 x+ B
x+ B 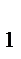 y + Cz
y + Cz 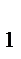 + D
+ D 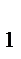 = 0,
= 0,
A  x+ B
x+ B 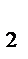 y + C
y + C 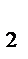 z + D
z + D 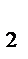 = 0 – общие уравнения прямой.
= 0 – общие уравнения прямой.
Угол между прямой, заданной в пространстве уравнением 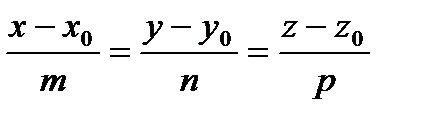 и плоскостью, заданной уравнением Ax+ By + Cz + D = 0, находится по формуле: sin
и плоскостью, заданной уравнением Ax+ By + Cz + D = 0, находится по формуле: sin 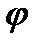 =
= 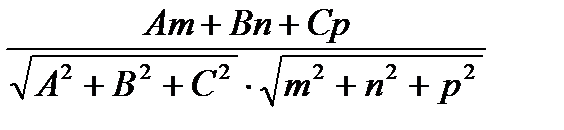 .
.
Расстояние d от точки M 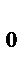 (x
(x 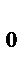 , y
, y 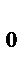 , z
, z 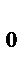 ) до плоскости, заданной уравнением Ax + By + Cz + D= 0 находится по формуле: d =
) до плоскости, заданной уравнением Ax + By + Cz + D= 0 находится по формуле: d = 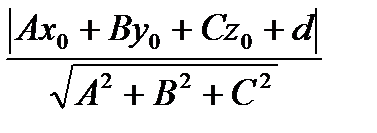 .
.
Тема 3. Введение в математический анализ
