Типовой расчет по теории вероятностей
Задача 1. Одновременно подбрасывают две игральные кости. В вариантах 1-10 найти вероятность того, что сумма выпавших очков 1) равна k; 2) меньше k+1; 3) больше k-1; 4) заключена в промежутке [a,b]. В вариантах 11-30 найти вероятность того, что произведение выпавших очков: 1) равно k; 2) меньше k+1; 3) больше k-1; 4) заключено в промежутке [a,b].
Задача 2. На некоторое обслуживающее устройство поступает две заявки. Каждая может поступить в любой момент времени в течение T минут. Время обслуживания первой заявки t1 минут, второй t2 минут. При поступлении заявки на занятое устройство она не принимается. При поступлении её хотя бы в последний момент времени T заявка обслуживается. Найти вероятность того, что 1) обе заявки будут обслужены; 2) будет обслужена одна заявка.
Задача 3. Задана электрическая схема системы, состоящей из пяти элементов. Событие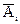 
отказ i-го элемента за некоторый промежуток времени. Вероятности безотказной работы элементов заданы:
P(Ai)=0.95, i=1,3,5; P(Ai)=0.9, i=2,4.
Событие A состоит в безотказной работе всей системы за рассматриваемый промежуток времени. Требуется: 1) Выразить событие A через Ai или 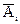(i=1,2,3,4,5); 2) найти вероятность P(A) безотказной работы системы.
Задача 4. Из партии, содержащей n изделий, среди которых k – высшего сорта, для контроля последовательно выбирают наугад m изделий. Найти вероятность того, что среди выбранных изделий окажется ровно l высшего сорта, при условии, что выборка производится: 1) с возвращением (выбранное изделие после проверки возвращается обратно в партию); 2) без возвращения (выбранное изделие в партию не возвращается).
Задача 5. На склад поступили детали, изготовляемые на трех станках. Изготовлено на станках деталей, %: на первом a, на втором – b, на третьем – c. Вероятность выпуска бракованных деталей на i-ом станке равна Pi(i=1,2,3). Определить вероятность того, что изделие, наудачу взятое со склада: 1) оказалось бракованным; 2) оказалось небракованным. Найти вероятность того, что оно изготовлено на j-м станке.
Задача 6. Произведено n выстрелов с постоянной вероятностью попадания при каждом выстреле, равной P.
Для случайной величины m (числа попаданий в цель) найти: 1) распределение вероятностей; 2) функцию распределения и построить её график; 3) вероятность попадания случайной величины в интервал ]a,b[; 4) найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины x.
Задача 7. Непрерывная случайная величина x имеет плотность вероятности f(x). Требуется; 1) найти её функцию распределения F(x); 2) построить графики функции распределения F(x) и плотности вероятности f(x); 3) вычислить вероятность попадания случайно величины в интервал ]a,b[; 4) найти математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины x.
Задача 8. Дана плотность вероятности f(x) случайной величины x . Случайная величина h связана со случайной величиной x функциональной зависимостью h=ax2+s. Найти: 1) математическое ожидание и дисперсию случайной величины h, используя плотность вероятности случайной величины x; 2) плотность вероятности случайной величины h и построить её график; 3) математическое ожидание и дисперсию случайной величины h , используя найденную плотность вероятности случайной величины h.
Задача 9. Дана система двух случайных величин (x, h) закон распределения которой задан таблицей, где x1=2, x2=3, x3=5, y1=-1, y2=0, y3=1, y4=2. Найти: 1) законы распределения случайных величин x и h; 2) математическое ожидания и дисперсии случайных величин x и h; коэффициент корреляции rxh ; условные распределения Px(xi|y2), Ph(yi|x2); 3) условные математические ожидания M(x|y2), M(h|x2)
Задача 10. Система непрерывных случайных величин (x, h) распределена равномерно в области D, ограниченной линиями x=a, y=b, y=b|x|a. Найти: 1) совместную плотность распределения f(x,y), предварительно построив область D; 2) плотность вероятности случайных величин x и h; 3) математическое ожидания и дисперсии случайных величин x и h; 4) коэффициент корреляции rxh ; 5) условные плотности распределения fx(x|y), fh(y|x); 6) условные математические ожидания M(x|y), M(h|x), линии регрессии и построить их графики.
Задача 11. Найти математическое ожидание и дисперсию случайной величины x =ax +bh+c, где (x, h) система случайных величин из задачи 10.
| Задача 1 | Задача 2 | Задача 3 | Задача 4 | |||||||
| Вариант | k | [a,b] | T | t1 | t2 | n | k | m | l | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| [4;6] |  | |||||||||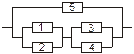
| [2;5] |  | |||||||||
| [3;7] |  | |||||||||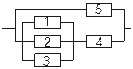
| [2;6] |  | |||||||||
| [3;5] |  | |||||||||
| [3;4] |  | |||||||||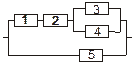
| [3;8] |  | |||||||||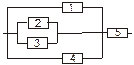
| [4;7] |  | |||||||||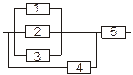
| [9;12] |  | |||||||||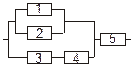
| [8;12] |  | |||||||||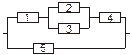
| [4;10] |  | |||||||||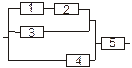
| [2;8] |  | |||||||||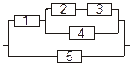
| [5;17] |  | |||||||||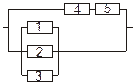
| [8;12] |  | |||||||||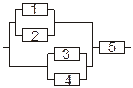
| [10;13] |  | |||||||||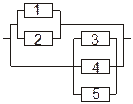
| [20;28] |  | |||||||||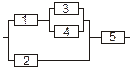
| [30;35] |  | |||||||||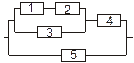
| [21;26] |  | |||||||||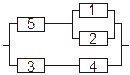
| [15;18] |  | |||||||||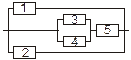
| [20;23] |  | |||||||||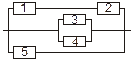
| [19;24] |  | |||||||||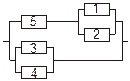
| [24;28] |  | |||||||||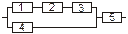
| [28;31] |  | |||||||||
| [21;36] |  | |||||||||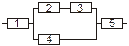
| [17;22] |  | |||||||||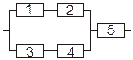
| [15;19] |  | |||||||||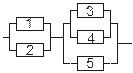
| [22;28] |  | |||||||||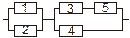
| [10;15] |  | |||||||||
| [12;18] |  | |||||||||
| [3;8] |  |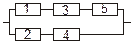
| Вар. | Задача 5 | Задача 6 | Задача 7 | ||||||||||
| a, % | b, % | c, % | P1 | P2 | P3 | j | n | P | ]a,b[ | f(x) | l | ]a,b[ | |
| 0.01 | 0.02 | 0.03 | 0.2 | ]1;0.5[ | Распеределение Релея f(x)=2l2xe^(-l2x2), x>0 | ]1;3[ | |||||||
| 0.01 | 0.04 | 0.03 | 0.3 | ]0.5;3[ | ]1/2;1[ | ||||||||
| 0.02 | 0.04 | 0.03 | 0.4 | ]1.5;2.5[ | ]2;3[ | ||||||||
| 0.03 | 0.01 | 0.05 | 0.5 | ]4.5;3[ | ]1/2;3[ | ||||||||
| 0.02 | 0.05 | 0.01 | 0.6 | ]0.5;3[ | ]1;2[ | ||||||||
| 0.01 | 0.03 | 0.02 | 0.7 | ]0.5;2[ | Распеределение Парето f(x)=l/2(2/x)^(l+1), x>2 | ]3;4[ | |||||||
| 0.03 | 0.03 | 0.04 | 0.8 | ]2;3.5[ | ]4;5[ | ||||||||
| 0.03 | 0.03 | 0.04 | 0.9 | ]1;3[ | ]4;8[ | ||||||||
| 0.05 | 0.05 | 0.03 | 0.1 | ]0.5;4[ | ]3;5[ | ||||||||
| 0.01 | 0.01 | 0.05 | 0.2 | ]-1;0.5[ | ]4;6[ | ||||||||
| 0.02 | 0.03 | 0.01 | 0.3 | ]0.5;3[ | Гамма-распределение f(x)=1/2 l3x2e^(-lx), x>0 | ]1;2[ | |||||||
| 0.03 | 0.01 | 0.04 | 0.4 | ]0.5;2.5[ | ]2;3[ | ||||||||
| 0.03 | 0.04 | 0.02 | 0.5 | ]1.5;3[ | ]1;3[ | ||||||||
| 0.05 | 0.01 | 0.03 | 0.6 | ]0.5;2[ | ]3;4[ | ||||||||
| 0.05 | 0.01 | 0.02 | 0.7 | ]1.3;2[ | ]2;4[ | ||||||||
| 0.02 | 0.01 | 0.03 | 0.8 | ]2;3.5[ | Экспоненциальное распределение f(x)=le^(-lx), x>0 | ]1;3[ | |||||||
| 0.03 | 0.01 | 0.02 | 0.9 | ]1;3[ | ]3;5[ | ||||||||
| 0.03 | 0.04 | 0.01 | 0.1 | ]3;4[ | ]3;4[ | ||||||||
| 0.03 | 0.02 | 0.04 | 0.2 | ]2;6[ | ]1;2[ | ||||||||
| 0.05 | 0.03 | 0.01 | 0.3 | ]1.5;4[ | ]2;5[ | ||||||||
| 0.05 | 0.02 | 0.01 | 0.4 | ]1;6[ | Распределение арксинуса f(x)=1/p(sqrt(l2-x2), l>x>-l | ]-2;2[ | |||||||
| 0.03 | 0.02 | 0.01 | 0.5 | ]2;7[ | ]0;1[ | ||||||||
| 0.04 | 0.01 | 0.03 | 0.6 | ]4;7[ | ]-1;1[ | ||||||||
| 0.04 | 0.02 | 0.03 | 0.7 | ]0.5;3[ | ]-3;0[ | ||||||||
| 0.01 | 0.03 | 0.05 | 0.8 | ]1;4[ | ]1;1/2[ | ||||||||
| 0.04 | 0.03 | 0.02 | 0.9 | ]-2;3[ | Распределение Лапласа (x)=1/2 le^(-l|x-3|), ¥>x>-¥ | ]2;3[ | |||||||
| 0.01 | 0.05 | 0.03 | 0.1 | ]0;2[ | ]1;3[ | ||||||||
| 0.04 | 0.03 | 0.025 | 0.2 | ]0.5;3[ | ]1;2[ | ||||||||
| 0.01 | 0.05 | 0.02 | 0.3 | ]-1;1.5[ | ]2;3[ | ||||||||
| 0.04 | 0.03 | 0.025 | 0.5 | ]2;4[ | ]1/2;1[ |
| Вар | Задача 8 | Задача 9 | Задача 10 x>0 | Задача 11 | |||||||||||||
| f(x) | a | b | x1 | x2 | x3 | a | b | a | b | a | b | c | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ||||
 
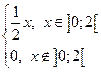|   | y1 y2 y3 y4 | 0.05 0.08 0.12 0.10 | 0.10 0.18 | 0.04 0.06 0.15 0.12 | -7 | |||||||||||
| 0.18 0.10 | 0.06 0.15 0.12 0.04 | 0.12 0.10 0.05 0.08 | -6 | -1 | |||||||||||||
| 0.18 0.10 | 0.15 0.12 0.04 0.06 | 0.10 0.05 0.08 0.12 | ½ | -5 | |||||||||||||
| 0.06 0.05 0.10 | 0.18 0.15 0.08 0.10 | 0.04 0.12 0.12 | -4 | -2 | |||||||||||||
| 0.18 0.15 0.08 0.10 | 0.04 0.12 0.12 | 0.06 0.05 0.10 | -2 | -3 | |||||||||||||
| 0.05 0.12 0.10 | 0.04 0.15 0.08 0.10 | 0.18 0.06 0.12 | -2 | -2 | -3 | ||||||||||||
| 0.05 0.08 0.18 | 0.12 0.04 0.10 0.06 | 0.10 0.15 0.12 | ½ | -2 | -2 | ||||||||||||
| 0.10 0.18 | 0.15 0.04 0.12 0.06 | 0.10 0.08 0.05 0.12 | -2 | -2 | |||||||||||||
| -1 | 0.04 0.12 0.06 0.10 | 0.08 0.05 0.12 | 0.10 0.18 0.15 | -2 | |||||||||||||
| -2 | 0.10 0.12 0.10 | 0.06 0.04 0.05 | 0.18 0.15 0.12 0.08 | -2 | -5 | ||||||||||||
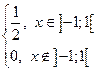 | y1 y2 y3 y4 | 0.04 0.06 0.02 0.08 | 0.10 0.15 0.05 0.20 | 0.06 0.09 0.03 0.12 | 1/2 | -6 | |||||||||||
| 0.15 0.05 0.10 0.20 | 0.06 0.02 0.04 0.08 | 0.09 0.03 0.06 0.12 | -5 | -6 | |||||||||||||
| 0.075 0.075 0.06 0.09 | 0.075 0.075 0.06 0.09 | 0.10 0.10 0.08 0.12 | -2 | -2 | -4 | ||||||||||||
| 0.06 0.06 0.04 0.04 | 0.06 0.06 0.04 0.04 | 0.18 0.18 0.12 0.12 | -2 | -2 | -3 | -7 | |||||||||||
| 0.03 0.04 0.01 0.02 | 0.09 0.12 0.03 0.06 | 0.18 0.24 0.06 0.12 | -2 | ½ | -2 | -2 | |||||||||||
| 0.09 0.12 0.03 0.06 | 0.09 0.12 0.03 0.06 | 0.12 0.16 0.04 0.08 | -1 | -3 | -8 | ||||||||||||
| 0.015 0.035 0.025 0.025 | 0.045 0.105 0.075 0.075 | 0.09 0.21 0.15 0.15 | -1 | -3 | |||||||||||||
| 0.02 0.03 0.07 0.08 | 0.07 0.105 0.245 0.28 | 0.010 0.015 0.035 0.040 | -1 | ½ | -3 | -7 | |||||||||||
| -1 | 0.030 0.045 0.105 0.120 | 0.050 0.075 0.175 0.200 | 0.02 0.03 0.07 0.08 | -1 | -3 | ||||||||||||
| -2 | y1 y2 y3 y4 | 0.06 0.045 0.075 0.120 | 0.04 0.03 0.05 0.08 | 0.100 0.075 0.125 0.200 | -1 | -2 | -3 | -6 | |||||||||
| | 0.12 0.10 0.18 0.08 | 0.15 0.10 | 0.04 0.06 0.12 0.05 | -1 | -2 | -5 | |||||||||||
| 0.05 0.08 0.12 0.10 | 0.18 0.06 | 0.15 0.12 0.10 0.04 | -1 | ½ | -2 | -4 | -5 | ||||||||||
| 0.18 0.06 0.12 | 0.12 0.05 0.10 | 0.15 0.04 0.10 0.08 | -1 | -2 | -3 | ||||||||||||
| 0.08 0.04 0.10 0.05 | 0.12 0.18 0.10 0.15 | 0.12 0.06 | -2 | -4 | |||||||||||||
| 0.08 0.05 0.10 0.12 | 0.04 0.12 0.15 0.06 | 0.10 0.18 | -1 | ||||||||||||||
| -1 | 0.10 0.06 | 0.18 0.12 0.15 0.10 | 0.04 0.08 0.05 0.12 | ½ | -4 | -3 | |||||||||||
| -1 | 0.18 0.12 0.15 0.10 | 0.04 0.08 0.05 0.12 | 0.06 0.10 | -4 | |||||||||||||
| -2 | 0.05 0.04 0.06 0.15 | 0.12 0.08 0.12 0.10 | 0.10 0.18 | -2 | -2 | -4 | -2 | ||||||||||
| -2 | 0.05 0.10 0.04 | 0.10 0.18 0.10 0.15 | 0.08 0.06 0.12 | -2 | -2 | -4 | |||||||||||
| -2 | -2 | 0.10 0.12 0.06 | 0.18 0.10 0.12 | 0.05 0.18 0.04 0.15 | -2 | ½ | -2 | -4 | -1 |
