Немного о потере решений в дифференциальных уравнениях

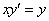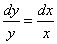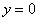В однородных уравнениях решение может потеряться в результате типовой замены и дальнейших сокращений, однако, на практике распространена и другая причина потери решений – это неосмотрительное деление. На самом деле с этим мы столкнулись в первом же примере вводного урока о дифференциальных уравнениях. В процессе решения уравнения «игрек» оказался в знаменателе: , но , очевидно, является решением ДУ и в результате неравносильного преобразования (деления) есть все шансы его потерять! Другое дело, что оно вошло в общее решение 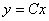при нулевом значении константы.

Аналогичная история с уравнением 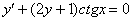Примера 3 того же урока, в ходе решения которого мы «сбросили» 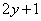в знаменатель. Строго говоря, следовало предварительно проверить, а не является ли 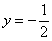решением данного диффура. Ведь является! Но и тут «всё обошлось», поскольку эта функция вошла в общий интеграл 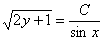при нулевом значении константы.

В действительности, конечно же, вовсе «не обошлось» – ситуация была под контролем, но я намеренно умолчал об этих нюансах на 1-ом уроке, чтобы не перегружать «чайников» информацией.

При неравносильных преобразованиях ВСЕГДА проверяйте (по крайне мере, устно), не теряете ли вы решения! Какие это преобразования? Чаще всего, сокращение на что-то или деление на что-то. Так, например, при делении на 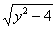нужно проверить, являются ли функции 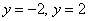решениями дифференциального уравнения. В то же время при делении на 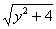необходимость в такой проверке уже отпадает – по причине того, что этот делитель не обращается в ноль.

Перечисленные тонкости также теряют актуальность, если в задаче требуется найти только частное решение (см., например, Пример №2 первого урока).

Следующий диффур – самостоятельно:

Пример 6

Решить дифференциальное уравнение

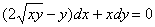
Полное решение и ответ в конце урока. Попробуйте для тренировки и здесь выразить общее решение.

В заключительной части урока рассмотрим еще пару характерных задач по теме:

Пример 7

Решить дифференциальное уравнение

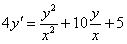
Решение: «любимая функция» 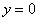не является решением, что убавляет хлопот. Идём проторенной дорогой. Данное уравнение является однородным, проведем замену:

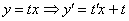
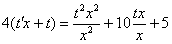
После замены проводим максимальные упрощения:

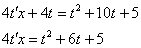
Разделяем переменные:

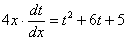
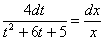
Интегрируем:

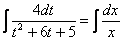
Интеграл левой части можно найти двумя способами: методом выделения полного квадрата или методом неопределенных коэффициентов. Как я уже отмечал, в диффурах удобнее использовать второй метод (если, конечно, многочлен можно разложить на множители)

Здесь многочлен на множители раскладывается: можно решить квадратное уравнение 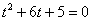, найти его корни и в результате: 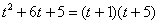. Опытные студенты способны выполнить подбор корней и устно.

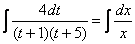
Методом неопределенных коэффициентов получим сумму дробей:

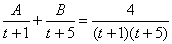
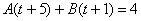
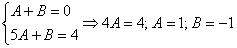
Таким образом:

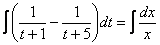
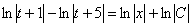
Получившийся общий интеграл упрощаем:

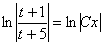
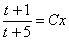
И только после упрощений выполняем обратную замену: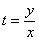

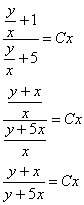
Ответ: общий интеграл: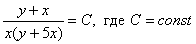

Пример 8

Решить дифференциальное уравнение

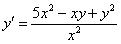
Это пример для самостоятельного решения. Отмечу, что время от времени однородное уравнение встречается в виде дроби, и типичный пациент выглядит примерно так: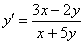

Наверное, многие обратили внимание, что во всех приведенных примерах мы не находили частные решения уравнений (задача Коши). Это не случайно. В практических заданиях
с однородными уравнениями частное решение требуют находить крайне редко, если честно, я даже не припомню таких случаев. Ну а если уж встретилась задача Коши в однородном уравнении, то, после изучения предыдущего урока, она не должна представлять для вас трудностей. Технология – точно такая же, как и для уравнений с разделяющимися переменными. Если уточнить, то почти всегда будут получаться не частные решения, а частные интегралы.

Существуют и более сложные однородные уравнения. Сложность состоит не в замене переменной или упрощениях, а в достаточно трудных или редких интегралах, которые возникают в результате разделения переменных. У меня есть примеры решений таких однородных уравнений – страшненькие интегралы и страшненькие ответы. Но о них не будем, иначе к большинству читателей во сне явится Александр Емелин известный персонаж с формулами на полосатом свитере.

И, для полноты картины, рекомендую изучить статью Линейные неоднородные дифференциальные уравнения.

Успешного продвижения!

Решения и ответы:

Пример 2: Решение: Проверим уравнение на однородность:
Вместо 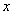подставляем 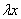, вместо 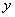подставляем :

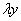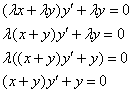
Все лямбды сократились, и получилось исходное уравнение, значит, данное ДУ является однородным.
Очевидно, что 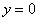является одним из решений данного уравнения.
Проведем замену: 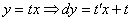и максимально упростим уравнение:

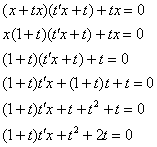
Разделяем переменные, слева собираем «тэ», справа – «иксы»:

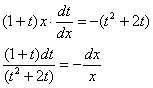
Интегрируем:

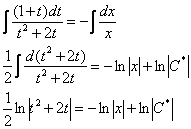
Надо сказать, с интегралом левой части повезло, бывает гораздо хуже.
Максимально упрощаем общий интеграл.
Если есть дроби, то от них лучше избавиться, умножаем каждую часть на 2:

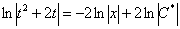
Константу 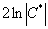я переобозначу через :

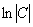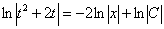
(Если этот момент не понятен, читайте статью Дифференциальные уравнения первого порядка)
Собираем в правой части всё под логарифм, затем избавляемся от логарифмов

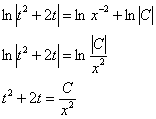
Обратная замена: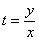

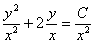
Умножаем все слагаемые на :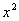

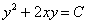
Ответ: общий интеграл: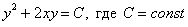

Примечание: Решение 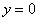входит в общее решение (когда 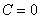), поэтому его не нужно дополнительно указывать в ответе.

Проверка: Дифференцируем общий интеграл:

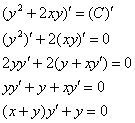
Получено исходное дифференциальное уравнение, значит, решение найдено верно.

Пример 4: Решение: Проверим уравнение на однородность:

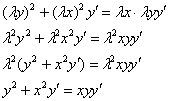
Таким образом, данное уравнение является однородным.
Очевидно, что 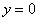является одним из решений уравнения.
Проведем замену:


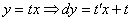
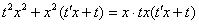
После подстановки проводим максимальные упрощения:

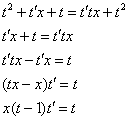
Разделяем переменные и интегрируем:

Новорожденный общий интеграл получен, здесь константу я не стал загонять под логарифм, в данном случае – это ни к чему. Использовать или не использовать этот прием с константой – понимание придет с опытом.
Упрощать особо нечего, поэтому проводим обратную замену: :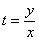

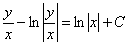
Общий интеграл можно упростить:

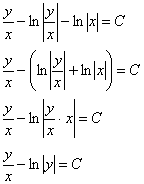
Ответ: общий интеграл: 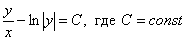. Ещё одно решение: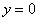
Примечание: здесь решение 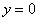не вошло в общий интеграл (т.к. не существует соответствующего значения константы), поэтому его следует указать дополнительно!

Пример 6: Решение: Преобразуем уравнение:

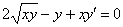
Очевидно, что 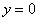является решением.
Данное уравнение является однородным, проведем замену:


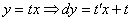
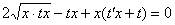
Максимально упрощаем:

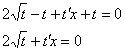
Разделяем переменные и интегрируем:

Упрощать нечего, поэтому проводим обратную замену :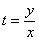

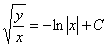
Ответ: общий интеграл: 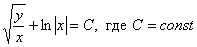. Ещё одно решение: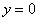

Примечание: также здесь можно выразить и общее решение: 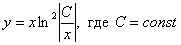, для этого сразу после интегрирования константу следует загнать под логарифм.

Пример 8: Решение: Данное ДУ является однородным, проведем замену: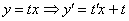





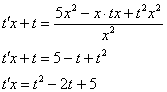
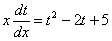
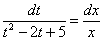
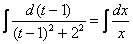
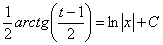
Обратная замена: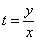

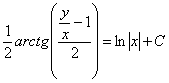
Ответ: общий интеграл: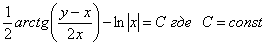

Линейные дифференциальные уравнения первого порядка.
Примеры решений

На данном уроке мы рассмотрим алгоритм решения третьего типа дифференциальных уравнений, который встречается практически в любой контрольной работе – линейные неоднородные дифференциальные уравнения первого порядка. Для краткости их часто называют просто линейными уравнениями. Материал не представляет особых сложностей, главное, уметь уверенно интегрировать и дифференцировать.

Начнем с систематизации и повторения.

На что в первую очередь следует посмотреть, когда вам предложено для решения любое дифференциальное уравнение первого порядка? В первую очередь необходимо проверить, а нельзя ли у данного диффура разделить переменные? Если переменные разделить можно (что, кстати, далеко не всегда очевидно), то нужно использовать алгоритмы и приемы решения, которые мы рассмотрели на первом уроке – Дифференциальные уравнения первого порядка. Советую посетить этот урок чайникам и всем читателям, которые чувствуют, что их знания и навыки в теме пока не очень хороши.

Если переменные в ДУ разделить не удалось, переходим к следующему этапу – проверяем, а не является ли уравнение однородным? Проверку обычно выполняют мысленно или на черновике, с самим алгоритмом проверки и образцами решения однородных уравнений можно ознакомиться на втором уроке – Однородные дифференциальные уравнения первого порядка.

Если переменные разделить не удалось, и уравнение однородным не является, то в 90% случаев перед вами как раз линейное неоднородное уравнение первого порядка.

Линейное уравнение первого порядка в стандартной записи имеет вид:

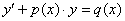
Что мы видим?
1) В линейное уравнение входит первая производная .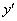
2) В линейное уравнение входит произведени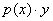е , где 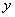– одинокая буковка «игрек» (функция), а 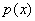– выражение, зависящее только от «икс».
3) И, наконец, в линейное уравнение входит выражение 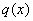, тоже зависящее только от «икс». В частности, 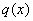может быть константой.

Примечание: Разумеется, в практических примерах эти три слагаемых не обязаны располагаться именно в таком порядке, их спокойно можно переносить из части со сменой знака.

Перед тем, как перейти к практическим задачам, рассмотрим некоторые частные модификации линейного уравнения.

– Как уже отмечалось, выражение 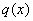может быть некоторой константой 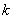(числом), в этом случае линейное уравнение принимает вид: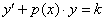

– Выражение 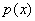тоже может быть некоторой константой 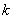, тогда линейное уравнение принимает вид: 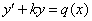. В простейших случаях константа равна +1 или –1, соответственно, линейное уравнение записывается еще проще: 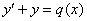или .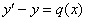

– Рядом с производной может находиться множитель 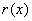, зависящий только от «икс»: 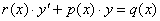– это тоже линейное уравнение.

Поехали.

Пример 1

Решить дифференциальное уравнение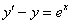

Решение: Данное уравнение является линейным и имеет простейший вид: 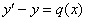.