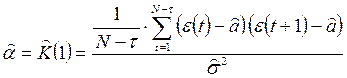Проверка гипотезы о наличии тренда во временном ряде
Даны значения временного ряда x(1), x(2),..., x(n). Необходимо определить, имеет ли этот ряд неслучайную компоненту, зависящую от времени - тренд.
Пусть xmed - выборочная медиана этого временного ряда. Образуем ряд z(1), z(2),..., z(n) следующим образом:
z(i) = знак(x(i) - xmed).
Серия - это группа подряд идущих +1 или -1.
Обозначим n(n) - количество серий; t(n) - длина самой протяжённой серии.
Критерий, основанный на выборочной медиане состоит в следующем:
если выполняются оба неравенства
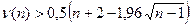
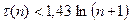
тогда с вероятностью, заключённой между 0,9025 и 0,95 делается вывод о неизменности среднего значения ряда и об отсутствии тренда. Если хотя бы одно из неравенств не выполняется, тогда с такой же вероятностью следует сделать вывод о наличии тренда.
Алгоритм скользящего среднего заключается в следующем:

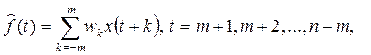
где wk – некоторые весовые коэффициенты, в сумме равные 1, т.е.
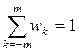
Для 2m+1 элементов временного ряда x(1), x(2),…, x(2m+1) строится полином степени p методом наименьших квадратов
значение этого полинома используют для расчёта значений оценки тренда 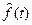 в средней точке этого отрезка ряда m + 1, т.е.
в средней точке этого отрезка ряда m + 1, т.е.
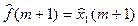
Эта же процедура выполняется для отрезка временного ряда x(2),…, x(2m+2).
Эта идея реализована в методе экспоненциально взвешенного скользящего среднего Брауна
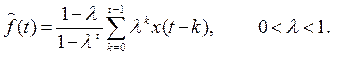
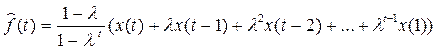
Дисперсия остаточной случайной компоненты после сглаживания
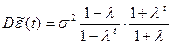
где
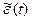 – остаточная нерегулярная компонента после сглаживания.
– остаточная нерегулярная компонента после сглаживания.
s2 = Dx(t);
поэтому при значениях l, не слишком близких к 1, и для достаточно удалённых от прошлого значений t случайные остатки 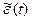 подвержены существенно меньшему разбросу.
подвержены существенно меньшему разбросу.
Рекуррентный способ вычисления сглаженных значений 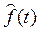 .
.
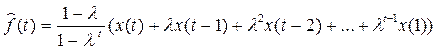 ;
;
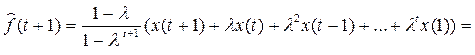
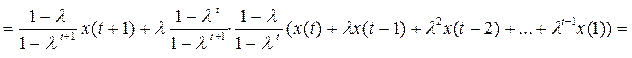
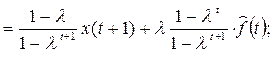
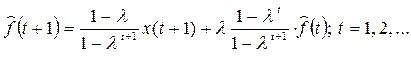
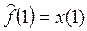
Среднее значение
Мe(t) = a;
дисперсия
De(t) = M(e(t) – a)2 = s2.
Оценки
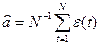
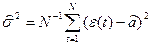
Так как значения временного ряда в моменты времени t, t + t являются случайными величинами, можно рассмотреть коэффициент корреляции между ними…
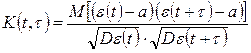
Корреляционной функцией стационарного временного ряда называется функция
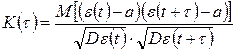
для стационарного временного ряда
De(t) = De(t + t) = s2,
поэтому
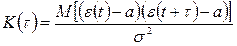
таким образом, корреляционная функция в точке t – это коэффициент корреляции между значениями ряда, отстоящими друг от друга на временной промежуток t.
Оценка корреляционной функции
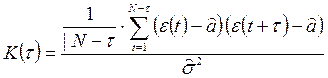
при сильной положительной зависимости e(t), e(t+t) в числителе будет много положительных слагаемых, и корреляционная функция будет иметь большое положительное значение; при сильной отрицательной зависимости (при e(t) > 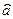 с большой вероятностью e(t) <
с большой вероятностью e(t) < 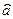 ) в числителе будет много отрицательных слагаемых, и корреляционная функция будет иметь малое отрицательное значение; при слабой зависимости e(t), e(t+t) примерно одинаковое количество слагаемых будут иметь положительные и отрицательные знаки, в это случае корреляционная функция будет мала по абсолютной величине.
) в числителе будет много отрицательных слагаемых, и корреляционная функция будет иметь малое отрицательное значение; при слабой зависимости e(t), e(t+t) примерно одинаковое количество слагаемых будут иметь положительные и отрицательные знаки, в это случае корреляционная функция будет мала по абсолютной величине.
1. 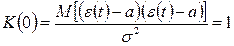 , что очевидно должно быть, так как измеряется коэффициент корреляции между одинаковыми случайными величинами.
, что очевидно должно быть, так как измеряется коэффициент корреляции между одинаковыми случайными величинами.
2. Чем больше t, т.е. сильнее разнесены во времени значения временного ряда e(t), e(t+t), тем слабее взаимосвязь между этими значениями, тем должна быть меньше по абсолютной величине K(t). Поэтому K(t) ® 0 при t ® ¥.
3. |K(t)|£1.
Для марковских процессов доказано, что
1) Me(t) = 0,
2) K(t) = at,
Таким образом, большое положительное (близкое к 1) значение a означает сильную коррелированность значений временного ряда, отстоящих на небольшое значение t, и медленное затухание этой зависимости с ростом t. Временной ряд при таких a имеет более плавный характер. При малом значении a степень зависимости значений временного ряда быстро уменьшается. При этом ряд имеет более изрезанный «дёрганный характер».
K(1) = a,
то есть величина a – это коэффициент корреляции соседних значений временного ряда.
3) 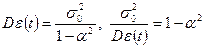
Из последнего соотношения следует, что, если значение |a| близко к 1, тогда дисперсия e(t) будет значительно больше дисперсии возмущения d(t). То есть, если соседние значения ряда e(t) сильно коррелированны, то ряд довольно слабых возмущений d(t) будет порождать размашистые колебания остатков e(t).
Из соотношения
K(1) = a,
следует способ идентификации модели авторегрессии 1-го порядка.
Оценка величины a формируется как оценка корреляционной функции в точке 1: