Момент импульса. Закон сохранения момента импульса
Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение[1].
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Определение[править | править исходный текст]
Момент импульса 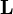 материальной точки относительно некоторого начала отсчёта определяется векторным произведением еёрадиус-вектора и импульса:
материальной точки относительно некоторого начала отсчёта определяется векторным произведением еёрадиус-вектора и импульса:
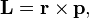
где 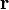 — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, 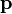 — импульс частицы.
— импульс частицы.
Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов:
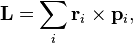
где 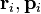 — радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
— радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется.
(В пределе количество частиц может быть бесконечным, например, в случае твердого тела с непрерывно распределенной массой или вообще распределенной системы это может быть записано как 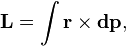 где
где 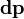 — импульс бесконечно малого точечного элемента системы).
— импульс бесконечно малого точечного элемента системы).
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Из определения момента импульса следует его аддитивность: как, для системы частиц в частности, так и для системы, состоящей из нескольких подсистем, выполняется:
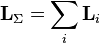 .
.
Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
В упрощённом виде: 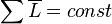 , если система находится в равновесии.
, если система находится в равновесии.
