Какие интегралы будут рассмотрены?
Сначала мы рассмотрим интегралы с корнями, для решения которых последовательно используется замена переменнойи интегрирование по частям. То есть, в одном примере комбинируются сразу два приёма. И даже больше.
Затем мы познакомимся с интересным и оригинальным методом сведения интеграла к самому себе. Данным способом решается не так уж мало интегралов.
Третьим номером программы пойдут такие интегралы от дробей, которых не было в предыдущих рахдела.
В-четвертых, будут разобраны дополнительные интегралы от тригонометрических функций. В частности, существуют методы, которые позволяют избежать трудоемкой универсальной тригонометрической подстановки.
И в заключении рассмотрим интеграл от корня, под которым находится дробь, а в числителе и знаменателе дроби – линейные функции.
Последовательная замена переменной и интегрирование по частям
Пример 1
Найти неопределенный интеграл
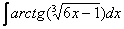 . Подынтегральная функция представляет собой арктангенс, под которым находится кубический корень. Первая же мысль, которая приходит в голову – избавиться бы от этого корня. Данный вопрос решается путем замены переменной, сама техника замены специфична, и она подробно рассмотрена на уроке Интегралы от иррациональных функций.
. Подынтегральная функция представляет собой арктангенс, под которым находится кубический корень. Первая же мысль, которая приходит в голову – избавиться бы от этого корня. Данный вопрос решается путем замены переменной, сама техника замены специфична, и она подробно рассмотрена на уроке Интегралы от иррациональных функций.
Проведем замену:
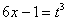 . После такой замены у нас получится вполне симпатичная вещь:
. После такой замены у нас получится вполне симпатичная вещь: 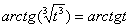 .
.
Осталось выяснить, во что превратится 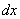 . Навешиваем дифференциалы на обе части нашей замены:
. Навешиваем дифференциалы на обе части нашей замены:
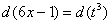 .
.
И, само собой, раскрываем дифференциалы:
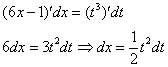 .
.
На чистовике решение кратко записывается примерно так:
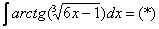 .
.
Проведем замену:
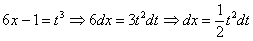 .
.
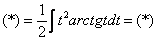 .
.
В результате замены получим интеграл, который интегрируется по частям:
 .
.
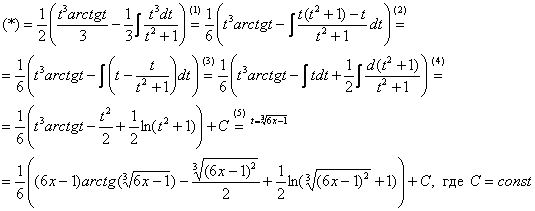
(1) Выносим (1/3) за скобки. К оставшемуся интегралу применяем прием, который рассмотрен в первых примерах урока статьи Интегрирование некоторых дробей.
(2) В подынтегральной функции почленно делим числитель на знаменатель.
(3) Используем свойство линейности неопределенного интеграла. В последнем интеграле сразу подводим функцию под знак дифференциала.
(4) Берём оставшиеся интегралы. Обратите внимание, что здесь в логарифме можно использовать скобки, а не модуль, так как 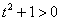 .
.
(5) Проводим обратную замену, выразив из прямой замены 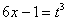 «тэ»:
«тэ»: 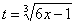 .
.
Как видите, в ходе решения пришлось использовать даже больше двух приемов решения, таким образом, для расправы с подобными интегралами нужны уверенные навыки интегрирования и не самый маленький опыт.
На практике, конечно же, чаще встречается квадратный корень, вот три примера для самостоятельного решения.
Пример 2
Найти неопределенный интеграл
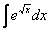 .
.
Пример 3
Найти неопределенный интеграл
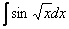 .
.
Пример 4
Найти неопределенный интеграл
 .
.
Данные примеры однотипны, поэтому полное решение в конце статьи будет только для Примера 2, в Примерах 3-4 – одни ответы. Какую замену применять в начале решений - очевидно. Но не всегда, когда под арктангенсом, синусом, косинусом, экспонентой и др. функциями находится корень из линейной функции, приходится применять сразу несколько методов. В ряде случаев удается «легко отделаться», то есть сразу после замены получается простой интеграл, который элементарно берётся. Самым легким из предложенных выше заданий является Пример 4, в нём после замены получается относительно несложный интеграл.
