Маршрутизация перевозок

Одной из важных задач оперативного планирования перевозок является составление маршрутов движения подвижного состава.

Маршрутизация перевозок называется составление рациональных маршрутов движения автомобилей, обеспечивающих сокращение непроизводительных холостых пробегов в целом по всему подвижному составу.

Задача составления рациональных маршрутов является особенно актуальной при перевозках массовых грузов.

К рациональным относятся маршруты, которые в сумме дают максимальный коэффициент использования пробега.

Рациональные маршруты разрабатываются различными методами, одним из которых является метод совмещённых матриц.

Метод совмещённых матриц

Согласно решению предыдущей задачи, поставщики должны обеспечить доставку грузов получателям в таком порядке: от поставщика А1 к получателям Б2–224 т и Б3–210 т; от А2 к Б1-434 т и Б4-196 т; от А3 к Б2-210.

Известны расстояния от поставщиков к получателям (таблица 3).

Таблица 3 – Исходные данные

Получатель	Расстояние от поставщиков, км
А1	А2	А3
Б1 Б2 Б3 Б4

Требуется составить маршруты работы подвижного состава таким образом, чтобы, не меняя порядок перевозки грузов от поставщиков к получателям, добиться наибольшего значения коэффициента использования пробега.

Решение. Исходные данные заносим в матрицу, которая является зашифрованным планом перевозок, т.е. планом, заявленным поставщиком (рисунок 10).

Потребитель	Вспомога- тельные	Поставщик
Строка Столбец	А1	А2	А3	Потребность вгрузет
Б1
Б2
Б3
Б4
Наличие груза, т

Рисунок 10. – Матрица №10 – Заданный план перевозок.

Решаем матрицу №10 аналогично тому, как это было сделано ранее при определении оптимального плана закрепления получателей за поставщиками. Такая матрица показана на рисунке 11 (матрица №11) и представляет собой оптимальный план движения автомобилей без груза, т.е. кратчайший путь возврата порожних автомобилей на пункты погрузки.

Потребитель	Вспомога- Тельные	Поставщик
Строка Столбец	А1	А2	А3	Потребность вгрузет
Б1
Б2
Б3
Б4
Наличие груза, т

Рисунок 11. – Матрица №11 – Оптимальный план возврата порожних автомобилей на пункты погрузки.

Для разработки рациональных маршрутов накладываем данные одной матрицы на другую: в матрицу №10 подставляем цифры из матрицы №11, причём цифры груза показаны в скобках, а без скобок – цифры плана возврата порожних автомобилей (матрица №12).

Потребитель	Вспомога- тельные	Поставщик
Строка Столбец	А1	А2	А3	Потребность вгрузет
Б1
(434)
Б2
		(434)
Б3
				(210)
Б4				(196)
Наличие груза, т

Рисунок 12. – Матрица №12 – Совмещённая матрица.

Составляя рациональные маршруты, следует учитывать следующие правила.

Правило 1. Если в клетках матрицы находятся две цифры в скобках и без них, то здесь имеет место маятниковый маршрут, причём число перемещаемого груза принимаем по наименьшей цифре.

На совмещённой матрице имеется лишь одна клетка А2Б4 в которой проставлены две цифры в скобках и без них. Загрузка в этой клетке равна 196 т. Груз от поставщика А2 будет доставляться получателю Б4 в количестве 196 т на расстояние 15 км и, разгрузившись, автомобили возвратятся опять на пункт погрузки А2.

Шифр маршрута будет следующий: А2Б4 - Б4А2.

А2 – Б4 – 15 км – 196 т;

Б4 – А2 – 15 км.

Коэффициент использования пробега:

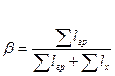, (11)

где 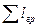- сумма длин груженой ездки.

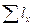- сумма длин холостой ездки.

Коэффициент использования пробега составит

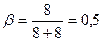
При дальнейшем рассмотрении использованные цифры из матрицы исключаются и в последующих распределениях не участвуют.

Для отыскания маршрутов работы подвижного состава строим контур.

Правило 2. Контур состоит из горизонтальных и вертикальных отрезков прямых, вершины которых должны лежать попеременно в загруженных клетках со скобками и без них; контур следует начинать из клетки с наименьшей загрузкой, независимо от наличия скобок, и вести его по кратчайшему пути.

Матрица с нанесённым на ней контуром, который охватывает клетки А1Б1 – А2Б1 – А2Б2 – А1Б2 – А1Б1, показана на рисунке 13.

Потребитель	Вспомога- тельные	Поставщик
Строка Столбец	А1	А2	А3	Потребность вгрузет
Б1
(434)
Б2
		(434)
Б3
				(210)
Б4
Наличие груза, т

Рисунок 13. – Матрица №13 с контуром маршрута.

Здесь имеет место кольцевой маршрут по схеме: из пункта А1 груз в количестве 224т будет направлен потребителю Б1 на расстояние 12 км; после разгрузки в пункте Б1 порожние автомобили будут направлены в пункт А2 на расстояние 6 км. В пункте А2 автомобили будут загружены грузом в количестве 224 т и направлены на расстояние 17 км в пункт Б2, откуда после разгрузки в холостую будут направлены в пункт А1 на расстояние 13 км.

Следовательно, шифр маршрута будет такой: А1Б1 – Б1А2 – А2Б2 – Б2А1.

А1 – Б1 – 12 км – 224 т; Б1 – А2 – 6 км;

А2 – Б2 – 17 км – 224 т; Б2 – А1 – 13 км.

Коэффициент использования пробега

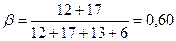
Количество перевезённого груза составит 448 т; из пункта А1 в Б1 – 224 т и из А2 в Б2 - 224 т.

Использованные цифры из матрицы исключаются.

Построение очередного кольцевого маршрута показано на рисунке 14.

Потребитель	Вспомога- тельные	Поставщик
Строка Столбец	А1	А2	А3	Потребность вгрузет
Б1
(210)		210
Б2
		(210)
Б3
210				(210)
Б4
Наличие груза, т

Рисунок 14. – Матрица №14 с контуром маршрута

Шифр маршрута: А1Б1 – Б1А2 – А2Б2 – Б2А3 – А3Б3 – Б3А1.

А1 – Б1 – 12 км – 210 т; Б1 – А2 – 6 км;

А2 – Б2 – 17 км – 210 т; Б2 – А3 – 5 км;

А3 – Б3 – 12 км – 210 т; Б3 – А1 – 8 км.

Общий пробег за оборот

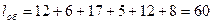км.

Гружёный пробег за оборот

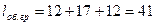км.

Коэффициент использования пробега на данном маршруте

.

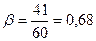Количество груза, перевезённом на данном маршруте, равно

210+210+210=630 т.

После использования всех имеющихся в матрице цифр задача на маршрутизацию перевозок считается законченной.