Второго порядка с правыми частями специального типа

Линейным неоднородным уравнением второго порядка с постоянными коэффициентами называется уравнение вида:

,

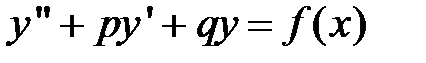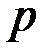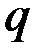где и – постоянные коэффициенты.

Теорема. Общее решение линейного неоднородного уравнения второго порядка находится по формуле:

, (1)

где 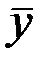– общее решение однородного дифференциального уравнения;

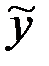– частное решение, определенное видом правой части неоднородного уравнения, то есть функции .

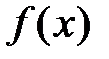Таким образом, чтобы найти общее решение неоднородного дифференциального уравнения нужно:

1) найти общее решение 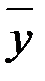соответствующего однородного уравнения;

2) найти любое частное решение 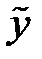неоднородного уравнения;

3) найденные решения сложить, найденная сумма и будет общим решением неоднородного уравнения.

Рассмотрим несколько случаев нахождения частных решений неоднородного дифференциального уравнения со специальными правыми частями.

1. Пусть в правой части уравнения функция 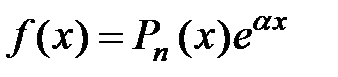, где 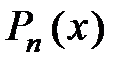– многочлен 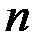-й степени.

В этом случае возможны такие ситуации:

а) число 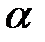не является корнем характеристического уравнения.

Тогда частное решение находится в виде:

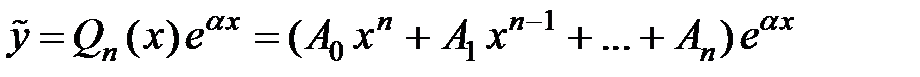, (2)

где 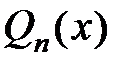– полный многочлен той же степени, что и 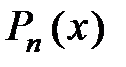. Коэффициенты этого многочлена неизвестны и находятся при подстановке решения в неоднородное уравнение в результате приравнивания коэффициентов, которые стоят при одинаковых степенях 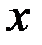в левой и правой частях уравнения. В этом заключается суть метода неопределенных коэффициентов;

б) число 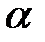совпадает с одним из корней характеристического уравнения: 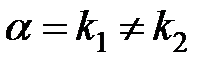.Тогда частное решение находится в виде:

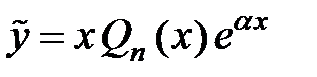; (3)

в) число 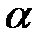совпадает с двукратным корнем характеристического уравнения: 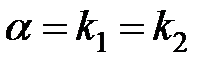.Тогда частное решение находится в виде:

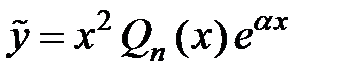. (4)

Пример 4. Найти решение дифференциального уравнения

,

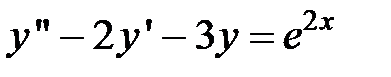которое удовлетворяет начальным условиям: ; .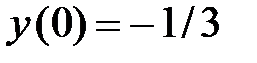

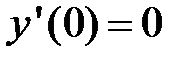Решение.

Определим общее решение данного дифференциального уравнения. Это линейное неоднородное дифференциальное уравнение, поэтому его общее решение состоит из общего решения соответствующего однородного уравнения и любого частного решения неоднородного уравнения.

Найдем общее решение однородного уравнения: .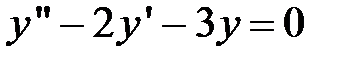

Составим его характеристическое уравнение: .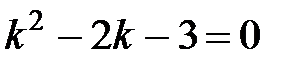

Это уравнение имеет разные действительные корни: 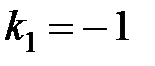; 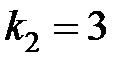, которым соответствуют два частных решения однородного уравнения: 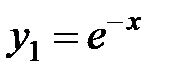и .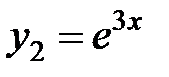

Общее решение однородного уравнения имеет вид:

.

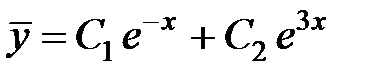Для нахождения частного решения неоднородного уравнения применим метод неопределенных коэффициентов. Будем искать частное решение неоднородного уравнения в виде: .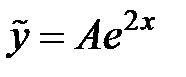

Для нахождения неизвестного коэффициента 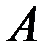подставим функцию 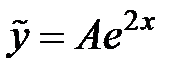и ее производные: 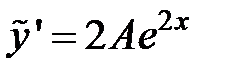и 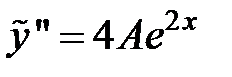в исходное неоднородное уравнение.

Имеем: 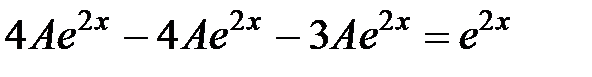, откуда .

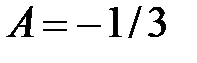Таким образом, общее решение неоднородного уравнения запишется так:

.

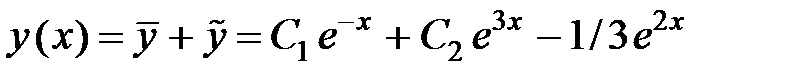Найдем частное решение неоднородного уравнения при начальных условиях: ; .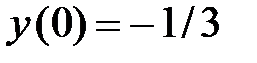

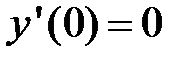Подставим: 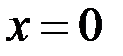, , 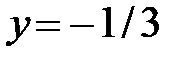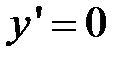в выражения для 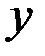и .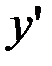

Если 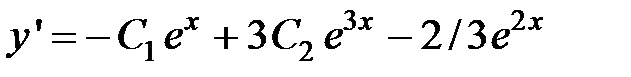, то получим:

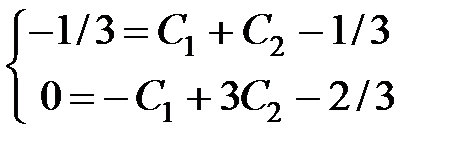, или .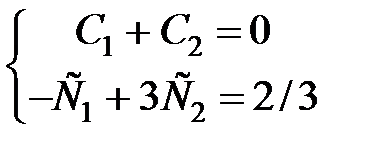

Откуда: , .

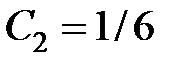Тогда искомое частное решение:

.

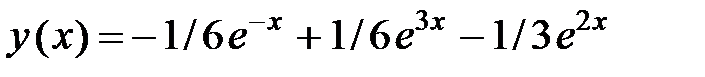Если правая часть уравнения 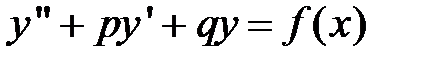имеет вид: 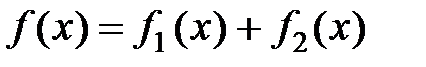, то частное решение этого уравнения может быть найдено, как сумма частных решений уравнений:

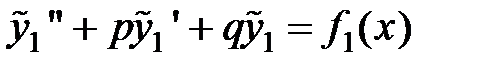
и

.

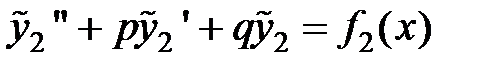То есть

.

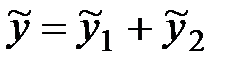Пример 5. Найти общее решение уравнения:

.

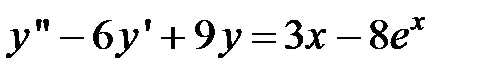Решение.

Записав характеристическое уравнение: 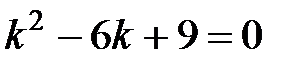, находим его корни: 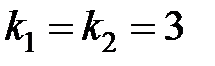. Общее решение соответствующего однородного уравнения имеет вид:

.

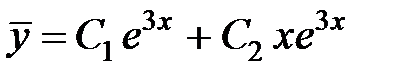Правая часть данного уравнения является суммой:

,

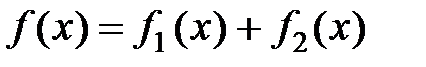где , .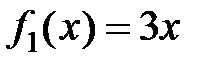

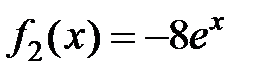Следовательно частное решение 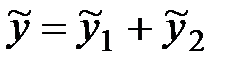, а именно:

.

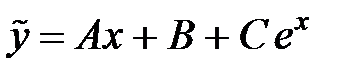Взяв первую и вторую производные от функции 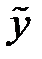и подставив их и саму функцию в исходное уравнение, получим:

.

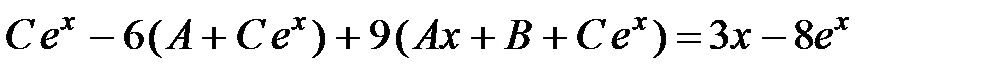Приравняем коэффициенты у подобных членов обеих частей полученного соотношения.

Получим систему линейных уравнений относительно неизвестных коэффициентов:

,

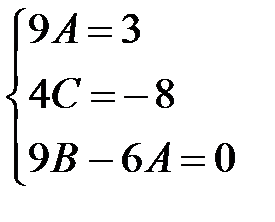решением которой являются:

, , .

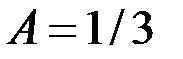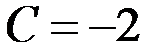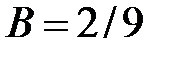Следовательно, .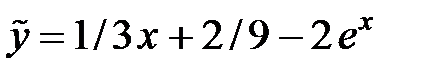

Таким образом, общее решение имеет вид:

.

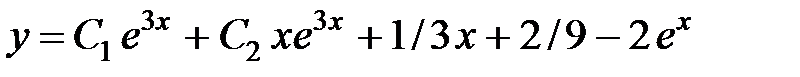2. Рассмотрим уравнение, которое имеет в правой части:

,

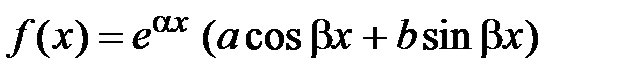где 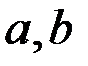– постоянные.

При таком виде функции 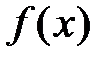могут быть два случая:

а) 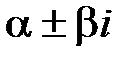не являются корнями характеристического уравнения. Тогда частное решение имеет вид:

,

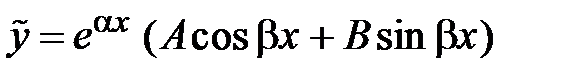где 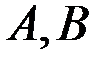определяются в результате приравнивания коэффициентов пр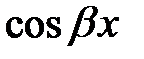и и 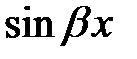в левой и правой частях уравнения при подстановке в это уравнение частного решения 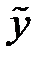и его первой и второй производных;

б) 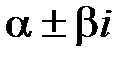совпадают с корнями характеристического уравнения. В этом случае:

.

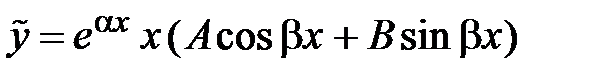При нахождении частного решения линейного неоднородного уравнения предлагаем пользоваться табл. 1.

Таблица 1