Исследование устойчивости системы с помощью критерия Михайлова

Содержание

курсовой работы по дисциплине " Теория автоматического управления",

тема "Исследование линейных САУ",

специальность 140604, группа ЭП-31

1) Содержание……………………………………………………...………..2

2) Введение…………………………………………………………………..3

3) Исходные данные…………………………………………...……………3

4) Структурные преобразования………………………………...…………4

5) Исследование устойчивости САУ в среде пакета Mathcad…………..5

6) Исследование устойчивости САУ в среде пакета MATLAB-Simulin.10

7) Анализ результатов……………………………………………………..16

8) Заключение………………………………………………………………17

9) Литература………………………………………………………..……..18

Введение.

Целью данной курсовой работы является исследование на устойчивость линейной САУ (системы автоматического управления). Анализ проводить различными методами: алгебраическими и частотными. При исследовании использовать два программных пакета Mathcad 14.0 и Matlab 6.5 с встроенным пакетом Simulink. На основе полученных данных сделать выводы о устойчивости системы линейной САУ и о том какие результаты выдали разные программные пакеты (совпали ли они).

Исходные данные.

Вариант № 2.

Исходная схема:

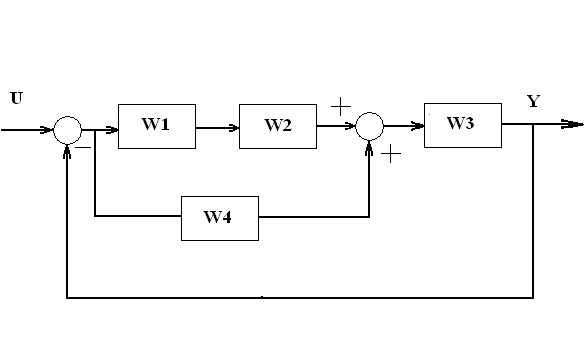
Значения передаточных функций звеньев:

W1	W2	W3	W4

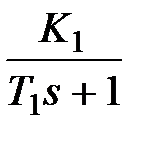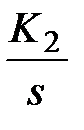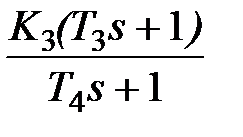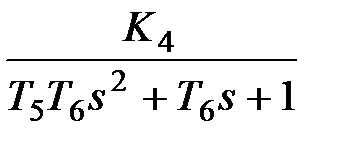Значения коэффициентов усиления:

, , , .

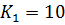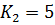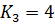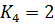Значения постоянных времени(с):

, , , ,

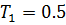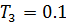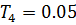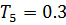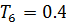
Структурные преобразования.

Эти преобразования нужны для упрощения исходной схемы и получения одной передаточной функции.

Подставим все имеющиеся числовые данные в формулы передаточных звеньев:

; ; ;

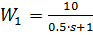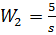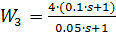Звено 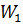соединено последовательно со звеном 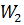. Их общая передаточная функция находится перемножением: .

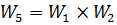Звено 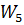параллельно звену 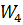по положительной связи. Их общая передаточная функция находится сложением: .

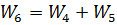Звено 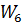соединено последовательно со звеном 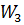. Их общая передаточная функция находиться перемножением: .

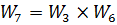Звено 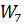имеет отрицательную обратную связь. Общая передаточная функция всей системы имеет вид: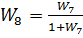

Исследование устойчивости линейной САУ в среде пакета Mathcad.

Найдем передаточную функцию системы используя структурные преобразования.

1) Первое преобразование:

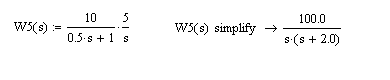
2) Второе преобразование:

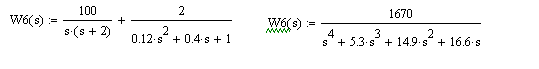
3) Третье преобразование:

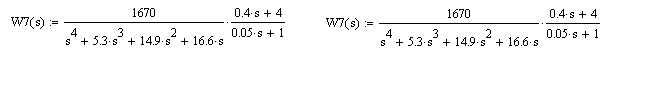
4) Четвертое преобразование:

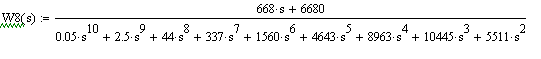
Получим основные характеристики исследуемой передаточной функции.

1) Заменим оператор s на jω и распишем функцию в виде коэффициентов b(ω), c(ω), d(ω), f(ω).

Теперь составим функции U(ω) и V(ω) по следующим формулам:

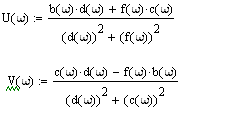
2) АФЧХ (разворот годографа) будет иметь вид:

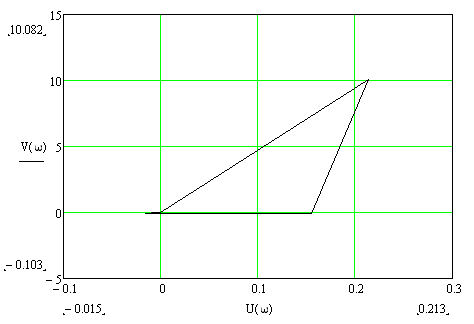
3) АЧХ имеет вид:

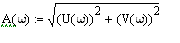
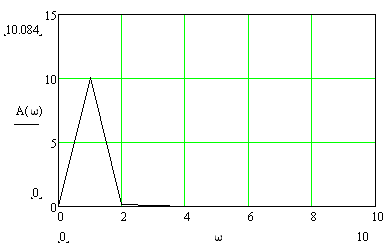
4) ФЧХ имеет вид:

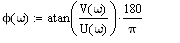
Т.к. ФЧХ имеет скачкообразный вид, вводим специальные уравнения сглаживающие эти скачки:

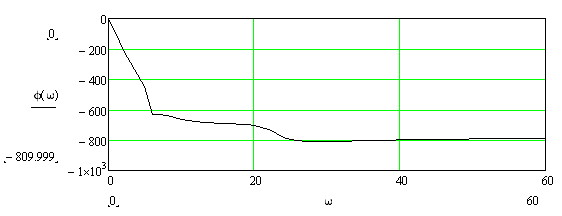
5) Логарифмическая характеристика имеет вид:

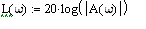
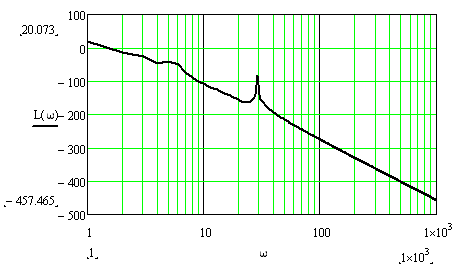
Найдем корни характеристического уравнения передаточной функции:

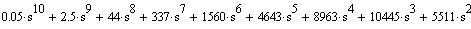
Корни:

Отметим данные корни на комплексной плоскости:

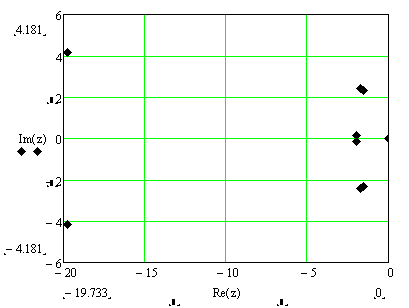
Из графика видно, что система находится на границе устойчивости (имеются корни на Re(z)=0).

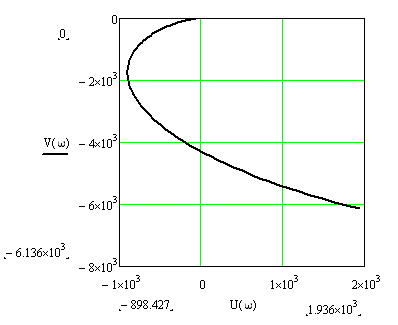
Исследование устойчивости системы с помощью критерия Михайлова.

На основе этого критерия система является устойчивой, если при изменении частоты от 0 до ∞ годограф характеристического вектора (кривая Михайлова) начинается на положительной части вещественной оси и последовательно обходит в положительном направлении n-квадрантов.

Знаменатель передаточной функции имеет вид:

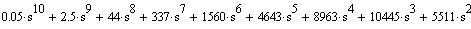
Выделим действительную и мнимую часть:

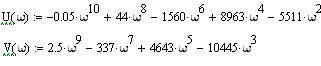
Построим годограф по ним при изменении ω от 0 до 1:

Полученный график говорит об неустойчивости системы.