Критерий устойчивости Михайлова

Рассмотрим характеристическое уравнение замкнутой системы n-ой степени с действительными коэффициентами.

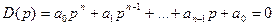(5-7)

где 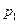, ,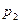…, 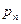- корни этого уравнения.

На комплексной плоскости корней (Рис. 5.1) каждому корню соответствует вполне определенная точка или две точки для сопряженных корней.

Рис 5.1 Комплексная плоскость корней.

Теоретически каждый корень 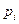изображается в виде вектора, проведенного из начало координат в точке 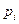. Длина этого вектора равна модулю комплексного числа 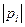, а угол, образованный вектором с положительным направлением действительной оси, аргументу или фазе комплексного числа – .

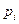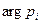Изменение положения корня в плоскости комплексного переменного ведет к изменению аргумента- .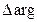

Положив 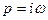в характеристическом уравнении 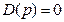, получим изменение аргумента вектора – .

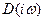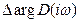Если все корни характеристического уравнения находятся слева от мнимой оси, то согласно теореме Ляпунова система будет устойчива, а при изменении частот 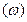вектор 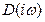будет поворачиваться в положительном направлении – против часовой стрелки. При изменении частот от -∞ до ∞ изменение вектора будет равно ,

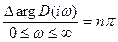где 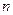- степень характеристического уравнения 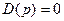, определяющая число его корней, 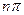- наибольшее изменение аргумента .

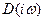При изменении от -∞ до ∞ вектор 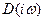на плоскости комплексного переменного описывает своим концом кривую, которая называется характеристической кривой или годографом вектора .

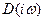Уравнение характеристической кривой можно найти, подставив 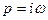в многочлен .

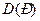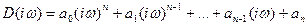(5-8)

Отделяя в нем действительную часть от мнимой, получим

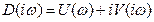(5-9)

где 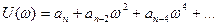- действительная часть,

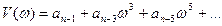- мнимая часть.

Действительная часть является четной функцией , все степени ее членов четные, начиная с нулевой (первый член 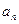), а мнимая 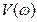- нечетной функцией .

Поэтому для отрицательных значений

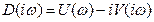(5-10)

Следовательно, характеристическая кривая симметрична относительно действительной оси, поэтому при построении характеристической кривой можно ограничится лишь положительными 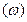от 0 до ∞, тогда угол поворота вектора 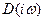, т.е. изменение аргумента 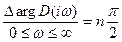, уменьшится вдвое.

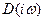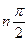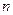Следовательно, критерий устойчивости можно сформулировать следующим образом: замкнутая АСР будет устойчива, если при возрастании от 0 до ∞ вектор повернется в положительном направлении на угол , где - степень характеристического уравнения 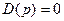или, что то же самое, если характеристическая кривая при изменении от 0 до ∞, начиная с положительной действительной оси, обходит последовательно в положительном направлении n-квадрантов комплексной плоскости.

В такой форме критерий устойчивости был предложен А.В.Михайловым в 1938 г.

Характеристическая кривая при изменении от 0 до ∞ будет обходить n квадрантов в положительном положении, если уравнения

;

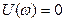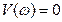
имеют все действительные и перемежающиеся корни, т.е. между каждыми двумя соседними корнями уравнения 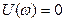лежит один корень уравнения 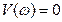и наоборот, между двумя соседними корнями уравнения 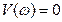лежит один корень уравнения .

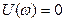Система будет находится на границе устойчивости, если характеристическая кривая при некотором значении пересекает начало координат, обходя при этом (n-1) квадрантов.(Рис. 5.2)

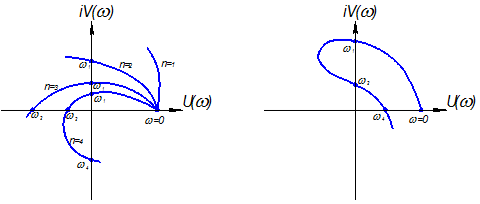
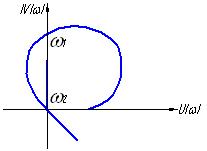
Рис 5.2 Характеристические кривые.

а) устойчивые системы б)неустойчивая система в) система на границе устойчивости.

Свойства годографа вектора :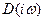

1) Годограф представляет кривую, всегда симметричную относительно действительной оси комплексной плоскости. Это следует из того, что 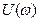- функция четная, а 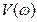- нечетная функция переменной .

2) При 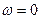годограф пересекает действительную ось в точке, отстоящей от начало координат на расстоянии, равном значению 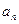-свободного члена характеристического уравнения.

3) Максимально возможное число пересечений полуветви годографа с действительной осью равно 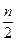, при 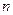- четном и 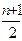, при нечетном, где 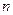- степень характеристического уравнения.

Значение , отвечающее точкам пересечения годографа с вещественной осью, определяются из уравнения .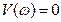

4) Максимально возможное число пересечений полуветви годографа с мнимой осью равно 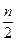при 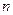- четном и 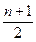при нечетном. Значение , отвечающее точкам пересечения годографа с мнимой осью, определяются из уравнения .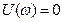

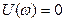Методы построения годографа Михайлова. 1) Характеристическая кривая строится последовательно, задаваясь значениями частот от 0 до ∞ в уравнения и .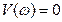

2) Метод контрольных точек, при котором построение характеристической кривой не обязательно. Вычисления ограничиваются нахождением только точек пересечения годографа с осями. Расположения этих точек позволяет судить об устойчивости системы. Их находят из уравнени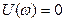й и 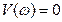и они должны быть перемежающимися.