Анықтамасы, түрлері, мысалдары
Айталық, V және V¢ – F өрісінде берілген векторлық кеңістіктер болсын.
Анықтама. Бір өрісте берілген V векторлық кеңістігін V¢ векторлық кеңістігіне бейнелейтін бейнелеуді оператор деп атайды.
Анықтама. Бір өрісте берілген V векторлық кеңістігін V¢ векторлық кеңістігіне бейнелейтін  операторы аддитивті және біртекті болса, оны сызықтық оператор дейді.
операторы аддитивті және біртекті болса, оны сызықтық оператор дейді.
 операторының аддитивтік шарты:
операторының аддитивтік шарты:
 а,b
а,b  V
V  (a + b) =
(a + b) =  (a ) +
(a ) +  (b),
(b),
 операторының біртектілік шарты:
операторының біртектілік шарты:
 а
а  V
V 

 F
F  (
(  a) =
a) = 
 (a).
(a).
Ескертулер:
1). Сызықтық оператордың аддитивтік және біртектілік шарттарын біріктіріп төмендегіше бір шарт етіп жазуға болады:
 а,b
а,b  V
V 
 ,
, 
 F
F  (
(  a +
a +  b) =
b) = 
 (a) +
(a) + 
 (b).
(b).
2). Сызықтық оператор гомоморфизм екені түсінікті.
3). Егер V¢ кеңістігі сан жиыны болса (Z,Q,R,C), онда сызықтық операторды сызықтық функционал деп атайды.
4). Егер V және V¢ кеңістіктері беттессе, онда V кеңістігінде берілген сызықтық операторды, кейде, сызықтық түрлендіру деп те атайды.
Осыларды ескеріп, векторлық кеңістікте берілген (анықталған) сызықтық оператордың анықтамасын былайша тұжырымдауға болады:
Анықтама.
def
(  : V
: V 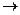 V –сыз. операт.)
V –сыз. операт.) 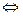 (
(  а,b
а,b  V
V 
 ,
, 
 F
F  (
(  a+
a+  b)=
b)= 
 (a)+
(a)+ 
 (b) )
(b) )
Бұл анықтамадан, векторлық кеңістікте берілген сызықтық оператор – сол кеңістіктің эндоморфизмі екені түсінікті.
Сызықтық оператордың анықтамадан шығатын 2 қарапайым қасиеттері бар:
1  .
.  =
=  = 0
= 0  F болса,
F болса,  ( 0 ) = 0
( 0 ) = 0  сызықтық оператор нольдік векторды орынында қалдырады (немесе сызықтық оператор нольдік векторды өз – өзіне көшіреді).
сызықтық оператор нольдік векторды орынында қалдырады (немесе сызықтық оператор нольдік векторды өз – өзіне көшіреді).
2  . Оператордың сызықтық болу шартын бірнеше векторлар үшін жалпылауға болады, яғни
. Оператордың сызықтық болу шартын бірнеше векторлар үшін жалпылауға болады, яғни
 (
( 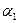 а
а  + ... +
+ ... + 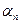 а
а  ) =
) = 

 (a
(a  ) + ... +
) + ... + 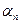
 (а
(а  ).
).
Мысалдар.
1). Кезкелген V векторлық кеңістігінде тепе – тең бейнелеу 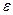 (х) = х (х
(х) = х (х  V) сызықтық оператор болады. Шынында да,
V) сызықтық оператор болады. Шынында да,
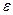 (
(  a +
a +  b) =
b) =  a +
a +  b =
b = 
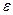 (a) +
(a) + 
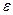 (b)
(b) 
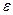 –сызықтық оператор.
–сызықтық оператор.
Оны бірлік оператордейді.
2). Кезкелген V векторлық кеңістігінің барлық векторын нольдік векторға көшіретін 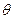 (х) =0(х
(х) =0(х  V) бейнелеуі де сызықтық оператор болады. Шынында да,
V) бейнелеуі де сызықтық оператор болады. Шынында да, 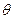 (
(  a+
a+  b) = 0= 0+ 0=
b) = 0= 0+ 0= 
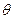 (a) +
(a) + 
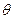 (b)
(b) 
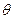 –сызықтық оператор.
–сызықтық оператор.
Оны нольдік оператордейді.
3). С 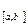 – үздіксіз функциялар кеңістігінде бейнелеу ретінде дифференциал- дау заңдылығын d(f ) = f ¢ алайық. Онда ол да сызықтық оператор болады. Шынында да, d(
– үздіксіз функциялар кеңістігінде бейнелеу ретінде дифференциал- дау заңдылығын d(f ) = f ¢ алайық. Онда ол да сызықтық оператор болады. Шынында да, d(  a +
a +  b) = (
b) = (  a +
a +  b)¢ = |дифференциалдау ережелері бойынша| =
b)¢ = |дифференциалдау ережелері бойынша| =  a¢ +
a¢ +  b¢ =
b¢ =  d(a)+
d(a)+  d(b)
d(b)  d–сызықтық оператор.
d–сызықтық оператор.
Оны дифференциалдау операторыдейді.
4). Айталық, V векторлық кеңістігі өзінің екі ішкі кеңістігінің тура қосындысы болсын: V = W 
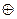 W
W  . Онда х = х
. Онда х = х  + х
+ х  бірмәнді өрнектелуіндегі
бірмәнді өрнектелуіндегі
х  – х векторының W
– х векторының W  -ге проекциясы ( W
-ге проекциясы ( W  -ге параллель) деп,
-ге параллель) деп,
х  – х векторының W
– х векторының W  -ге проекциясы ( W
-ге проекциясы ( W  -ге параллель) деп аталады.
-ге параллель) деп аталады.
х векторына х  векторын сәйкестікке қоятын заңдылықты қарастырайық. Оны V кеңістігін W
векторын сәйкестікке қоятын заңдылықты қарастырайық. Оны V кеңістігін W  ішкі кеңістігіне (W
ішкі кеңістігіне (W  -ге параллель) проекциялау деп атап,
-ге параллель) проекциялау деп атап, 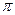 деп белгілейді:
деп белгілейді: 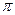 (х) = х
(х) = х  .
.
(Сәйкесінше, 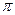 (х) = х
(х) = х  алынса, ол V кеңістігін W
алынса, ол V кеңістігін W  ішкі кеңістігіне (W
ішкі кеңістігіне (W  -ге параллель) проекциялау болады).
-ге параллель) проекциялау болады).
Қосынды тура қосынды болғандықтан, әрбір х векторы үшін х  бірмәнді анықталады. Сондықтан
бірмәнді анықталады. Сондықтан 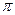 заңдылығы, шынында да, бейнелеу болады. Осы
заңдылығы, шынында да, бейнелеу болады. Осы 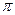 бейнелеуі сызықтық оператор болатынын өзіңіз тексеріңіз.
бейнелеуі сызықтық оператор болатынын өзіңіз тексеріңіз.
Оны проекциялау операторыдейді.
5). F өрісінде берілген кезкелген V векторлық кеңістігінде, тұрақтандырылған 
 F скаляры үшін,
F скаляры үшін,  (х) =
(х) =  х (х
х (х  V) бейнелеуі де сызық- тық оператор болады. (Тексеріңіз).
V) бейнелеуі де сызық- тық оператор болады. (Тексеріңіз).
Оны ұқсастық операторыдейді.
