Приклади для самостійного розв’язання
Розв’язати матричним способом системи рівнянь:
1. 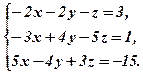 2.
2. 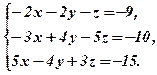
Розв’язати матричні рівняння
3. 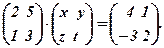 4.
4. 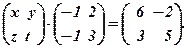
5.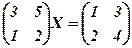 .6.
.6. 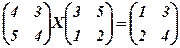 .
.
7.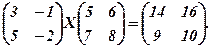
Відповіді. 1. . 2. . 3. .
4. . 5. . 6. . 7. .
Ранг матриці
Означення 1. Визначник, складений із елементів матриці 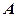 розміру
розміру 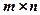 , які знаходяться на перетині довільних її
, які знаходяться на перетині довільних її 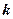 рядків і
рядків і 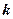 стовпців, називається мінором
стовпців, називається мінором 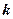 -того порядку даної матриці.
-того порядку даної матриці.
Для даної матриці можна складати мінори різних порядків, починаючи від 1 (визначник першого порядку приймається рівним своєму єдиному елементу) до меншого із чисел 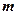 або
або 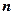 . Так для матриці
. Так для матриці
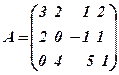 .
.
Можна скласти 12 мінорів першого порядку (самі елементи), 18 мінорів другого порядку і 4 мінори третього порядку. Випишемо мінори 3-го порядку, знайшовши їх значення (останнє пропонуємо перевірити самостійно)
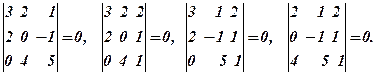
Серед мінорів другого порядку можуть бути нульові і відмінні від нуля. (Всі їх ми виписувати не будемо).
Наприклад, 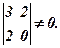
Означення 2. Найвищий порядок мінора матриці 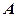 , відмінного від нуля, називається рангомцієї матриці і позначається
, відмінного від нуля, називається рангомцієї матриці і позначається 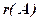 .
.
Із означення випливає, що якщо ранг матриці 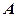
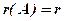 , то серед мінорів
, то серед мінорів 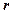 -того порядку є відмінні від нуля мінори, а всі мінори
-того порядку є відмінні від нуля мінори, а всі мінори 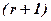 -го порядку дорівнюють нулю.
-го порядку дорівнюють нулю.
Якщо ж матриця нульова, то її ранг дорівнює нулю. Якщо матриця квадратна і невироджена, то її ранг дорівнює порядку матриці. Таким чином, для кожної матриці 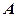 розміру
розміру 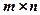 її ранг приймає відповідне значення
її ранг приймає відповідне значення 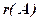 , яке знаходиться в межах
, яке знаходиться в межах
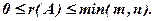
В наведеному вище прикладі матриці ми бачили, що найвищий порядок її мінора, відмінного від нуля, дорівнює 2, 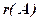 =2.
=2.
Знаходження ранга матриці шляхом перебору значень всіх її можливих мінорів пов’язано із значним обсягом обчислень, особливо коли розмір матриці великий. Тому існує простіший спосіб знаходження рангу, заснований на елементарних перетвореннях.
До елементарних перетворень матриці відносяться:
1) транспонування матриці;
2)множення елементів рядка (стовпця) матриці на число відмінне від нуля;
3)перестановка місцями двох рядків (стовпців);
4)додавання до елементів одного рядка (стовпця) відповідних елементів другого рядка (стовпця) помножених на одне й те ж саме число.
Теорема. При елементарних перетвореннях ранг матриці не змінюється.
Означення 3. Дві матриці 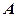 і
і 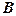 називаються еквівалентними (позначається
називаються еквівалентними (позначається 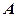 ~
~ 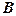 ), якщо одна з них може бути отримана з іншої за допомогою скінченого числа елементарних перетворень.
), якщо одна з них може бути отримана з іншої за допомогою скінченого числа елементарних перетворень.
Ранги еквівалентних матриць рівні,
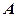 ~
~ 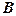
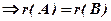 .
.
Приклад 1. Знайти ранг матриці
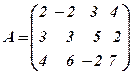 .
.
Розв’язання. Із другого рядка матриці 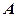 віднімемо перший і переставимо їх місцями:
віднімемо перший і переставимо їх місцями:
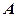 ~
~ 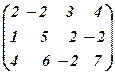 ~
~ 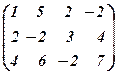 .
.
Додамо до ІІ-го і ІІІ-го рядків перший, відповідно помножений на –2 і –4, а тоді поміняємо місцями ІІ-ий і ІІІ-ій стовпці, отримаємо:
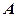 ~
~ 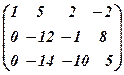 ~
~ 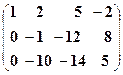 .
.
Помножимо ІІ-ий рядок на –10 і додамо з ІІІ-м рядком:
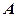 ~
~ 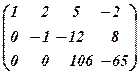
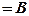 .
.
Матриця 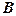 є трапецієподібною. Вона отримана з
є трапецієподібною. Вона отримана з 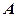 за допомогою скінченого числа елементарних перетворень, її ранг дорівнює 3.
за допомогою скінченого числа елементарних перетворень, її ранг дорівнює 3.
Таким чином,
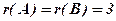 .
.
Зауважимо, що ранг матриці можна знаходити, якщо скористатись правилом прямокутника (див. 1.1), яке по суті відповідає послідовному застосуванню елементарних перетворень матриць 1) - 4).
Приклад 2.Знайти ранг матриці
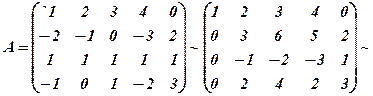
Помножимо ІІІ-ій рядок на (-1) і переставимо його з ІІ-м, провідним елементом виберемо 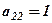
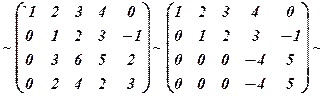
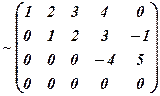 .
.
Очевидно що ранг останньої, а значить, і еквівалентної їй початкової матриці А дорівнює 3, тобто 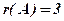 .
.
Зауваження. При знаходжені рангу матриці великого розміру раціональніше використовувати ЕОМ, застосовуючи відносно простий алгоритм правила прямокутників.
Знайти ранг матриць
1. . 2. .
3. . 4. .
Відповіді. 1. 2. 2. 2. 3. 3. 4. 3.
1.15.Лінійна залежність та лінійна незалежність рядків (стовпців) матриці
Зупинимось ще на відомому вже в 1.14. прикладі матриці
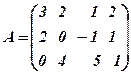 .
.
Там було встановлено, що ранг 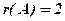 . Це означає, що один з рядків (стовпців) може бути записаний у вигляді лінійної комбінації двох інших. Для цього позначимо рядки матриці
. Це означає, що один з рядків (стовпців) може бути записаний у вигляді лінійної комбінації двох інших. Для цього позначимо рядки матриці  :
:
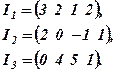
Покажемо, що можна знайти числа 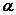 і
і 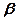 такими, що
такими, що
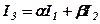 . (1)
. (1)
Дійсно, підставивши в (1) вирази для 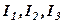 маємо:
маємо:
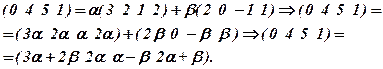
Відомо, що два рядки рівні, якщо в них рівні відповідні елементи, тобто
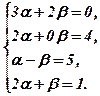 (2)
(2)
Із системи (2) знаходимо: 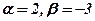 . Таким чином,
. Таким чином,
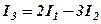 ,
,
або ще будемо говорити, що рядок 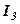 є лінійною комбінацією рядків
є лінійною комбінацією рядків 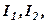 або ж рядок
або ж рядок 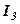 лінійно залежить від рядків
лінійно залежить від рядків 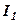 і
і 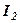 .
.
Перейдемо до означення понять лінійної залежності і лінійної незалежності рядків (стовпців) матриці 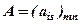 в загальній формі.
в загальній формі.
Нехай
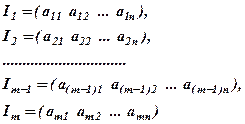
– рядки матриці 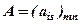 , і нехай
, і нехай
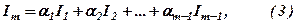
де 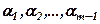 – деякі числа. Будемо говорити, що
– деякі числа. Будемо говорити, що 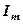 , тобто
, тобто
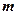 -ий рядок матриці
-ий рядок матриці 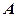 , лінійно виражаєтьсячерез перші
, лінійно виражаєтьсячерез перші 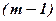 рядки цієї матриці, або що
рядки цієї матриці, або що 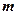 -ий рядок є лінійною комбінацією рядків
-ий рядок є лінійною комбінацією рядків 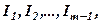 або ж, що рядок
або ж, що рядок 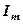 лінійно залежитьвід рядків
лінійно залежитьвід рядків 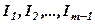 .
.
Рівність (3) можна переписати у вигляді
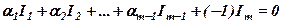 ,
,
де нуль в правій частині означає нульовий рядок.
Означення. Рядки 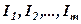 матриці
матриці 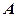 називаються лінійно залежними, якщо існують такі числа
називаються лінійно залежними, якщо існують такі числа 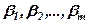 , не рівні одночасно нулю, що
, не рівні одночасно нулю, що
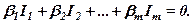 (4)
(4)
Якщо ж рівність (4) виконується тільки за умови, що всі коефіцієнти 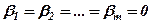 , то рядки
, то рядки 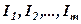 називаються лінійно незалежними.
називаються лінійно незалежними.
Ми вже відмічали, що якщо один з рядків матриці лінійно виражається через інші, то вони лінійно залежні. Навпаки, якщо має місце лінійна залежність (4) і при цьому хоча б один з коефіцієнтів, наприклад, 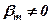 , то
, то
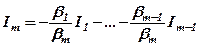 ,
,
тобто 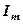 лінійно виражається через
лінійно виражається через 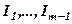 .
.
Аналогічним чином можна ввести поняття лінійної залежності і лінійної незалежності стовпців матриці 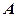 .
.
Теорема (про лінійну залежність і лінійну незалежність).
Якщо ранг матриці 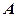 дорівнює
дорівнює 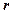 , то в цій матриці можна знайти
, то в цій матриці можна знайти 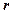 лінійно незалежних між собою рядків (стовпців), через які лінійно виражаються всі інші її рядки (стовпці).
лінійно незалежних між собою рядків (стовпців), через які лінійно виражаються всі інші її рядки (стовпці).
Наслідок 1. Максимальне число лінійно незалежних стовпців матриці дорівнює максимальному числу лінійно незалежних рядків, тому що при транспонуванні матриці її рядки стають стовпцями, а ранг при цьому не міняється.
Наслідок 2. Для того, щоб визначник дорівнював нулю, необхідно і досить, щоб його рядки (стовпці) були лінійно залежними.
1.16. Умови сумісності системи лінійних рівнянь. Теорема Кронекера – Капеллі[3]
Дослідимо в загальному вигляді систему 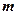 лінійних рівнянь з
лінійних рівнянь з 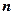 невідомими
невідомими 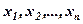 (
( 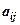 – задані коефіцієнти):
– задані коефіцієнти):
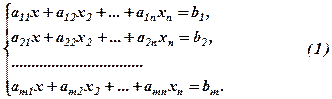
Розв’язком системи (1) називається сукупність чисел 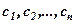 , яка будучи підставленою в кожне з рівнянь цієї системи замість невідомих
, яка будучи підставленою в кожне з рівнянь цієї системи замість невідомих 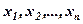 , перетворює її в тотожність.
, перетворює її в тотожність.
Система вигляду (1) називається сумісною, якщо вона має хоча б один розв’язок. Якщо система (1) не має розв’язку, то вона називається несумісною. Питання сумісності або несумісності системи можна розв’язати за допомогою ранга матриці.
Розглянемо матриці:
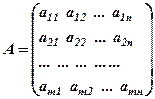 ,
, 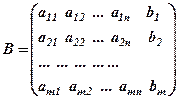 .
.
Матриця 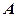 називається основною або матрицеюсистеми (1),
називається основною або матрицеюсистеми (1), 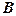 – розширеною матрицею. Позначимо їх ранги
– розширеною матрицею. Позначимо їх ранги 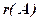 і
і 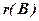 . Відмітимо, що
. Відмітимо, що 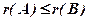 , тому що елементи матриці
, тому що елементи матриці 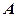 містяться серед елементів матриці
містяться серед елементів матриці 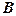 .
.
Умови сумісності чи несумісності системи лінійних рівнянь (1) виражаються наступною теоремою.
Теорема 1. (Кронекера – Капеллі). Для того щоб система лінійних рівнянь (1) було сумісною, необхідно і досить, щоб ранг матриці системи 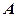 дорівнював рангу розширеної матриці
дорівнював рангу розширеної матриці 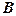 , тобто
, тобто 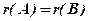 .
.
Із теореми випливає, що якщо 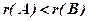 , то система несумісна.
, то система несумісна.
Сумісна система може мати єдиний розв’язок і тоді вона називається визначеною, або система може мати нескінченне число розв’язків і тоді вона називається невизначеною.
Теорема 2. Сумісна система (1) має єдинийрозв’язок, якщо 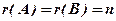 (ранги дорівнюють числу невідомих); якщо
(ранги дорівнюють числу невідомих); якщо 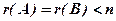 , то система має нескінченне число розв’язків.
, то система має нескінченне число розв’язків.
Вправи. Дослідити кожну із систем рівнянь і у випадку сумісності розв’язати її:
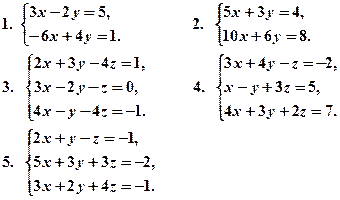
Відповіді: 1. Система несумісна. 2. Система має нескінченне число розв’язків, загальний розв’язок 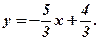 3. (1, 1, 1). 4. Система несумісна.
3. (1, 1, 1). 4. Система несумісна.
5. Система має нескінченне число розв’язків, загальний розв’язок: 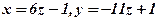 .
.
[1] К..Гаусс(1777-1855)-німецький математик,фізик,астроном
[2] Г. Крамер (1704 - 1752) - швейцарський математик.
[3] Л. Кронекер (1823 – 1891) – німецький математик,
А. Капеллі (1855 – 1910) – італійський математик.
