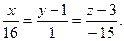Задачі для самостійного розв’язання
1.Скласти рівняння прямої , що проходить через точки А(-2,1,0) і В(0,1,3), та знайти координати її напрямного вектора.
2.Дано рівняння руху точки М(x,y,z): 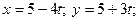
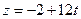 . Знайти: а) координати точки
. Знайти: а) координати точки 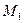 через 10 секунд від початку руху (t=0); б) довжину пройденого точкою шляху S за проміжок часу від t=0 до t=10с; в) величину швидкості; г) канонічне рівняння траєкторії руху.
через 10 секунд від початку руху (t=0); б) довжину пройденого точкою шляху S за проміжок часу від t=0 до t=10с; в) величину швидкості; г) канонічне рівняння траєкторії руху.
3.Знайти координати точок перетину прямої 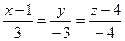 з координатними площинами. Побудувати пряму.
з координатними площинами. Побудувати пряму.
4.Звести до канонічного рівняння прямих:
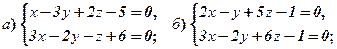
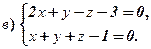
5.Перейти від загального рівняння прямої 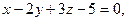
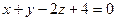 до канонічного та знайти точки перетину з координатними площинами.
до канонічного та знайти точки перетину з координатними площинами.
6.Скласти рівняння прямої, яка проходить через дві точки А(1,-3,1), В(2,4,5).
7.Скласти рівняння сторін трикутника з вершинами А(7,2,-6), В(11,-3,5), С(-3,4,-2) і рівняння його медіани, яка виходить з вершини В.
8.Знайти кути між прямими: 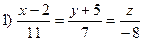 і
і 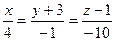 ; 2)
; 2) 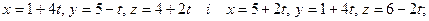
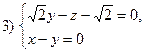 і
і 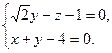
9.Скласти рівняння прямої, яка проходить через точку
М(2,-4,3) і паралельна прямій 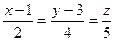 .
.
10.Скласти рівняння прямої, яка проходить через точку
А(2,-6,-9) паралельно прямій 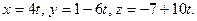
11.Скласти рівняння прямої, яка проходить через точку
В(1,-2,6) і паралельна прямій 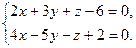
12.Показати, що прямі 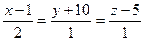 і
і 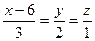 перетинаються і знайти їх точку перетину
перетинаються і знайти їх точку перетину 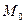 .
.
Вказівка. Нехай прямі 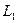 і
і 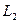 задані відповідно рівняннями
задані відповідно рівняннями 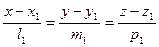 і
і 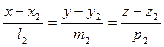 . Необхідною і достатньою умовою перетину двох непаралельних прямих є компланарнітсь трьох векторів
. Необхідною і достатньою умовою перетину двох непаралельних прямих є компланарнітсь трьох векторів 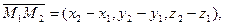
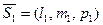 і
і 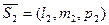 , тобто
, тобто
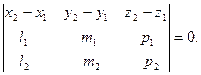
Для знаходження точки перетину прямих 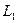 і
і 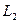 записати їх рівняння в параметричному вигляді з параметрами
записати їх рівняння в параметричному вигляді з параметрами 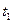 і
і 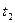 - відповідно і розв’язати систему рівнянь:
- відповідно і розв’язати систему рівнянь: 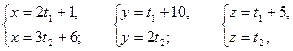 Знайшовши спочатку
Знайшовши спочатку 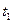 і
і 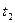 , а тоді x, y, z.
, а тоді x, y, z.
13.Скласти рівняння бісектриси кута К трикутника з вершинами К(0,1,3), L(4,4,-9), M(12,-3,0).
Вказівка. Знайти напрямні вектори 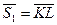 і
і 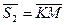 . За напрямний вектор
. За напрямний вектор 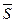 бісектриси можна взяти вектори
бісектриси можна взяти вектори 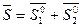 , де
, де 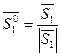 і
і 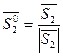 - орти відповідних векторів
- орти відповідних векторів 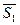 і
і 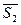 . Підкреслимо, що на векторах
. Підкреслимо, що на векторах 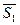 і
і 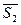 можна побудувати паралелограм, а на одиничних векторах
можна побудувати паралелограм, а на одиничних векторах 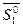 і
і 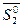 будується ромб, діагональ якого
будується ромб, діагональ якого 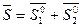 є бісектрисою кута.
є бісектрисою кута.
Відповіді. 1. 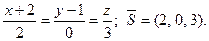
2. 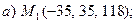
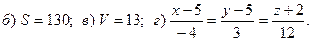 3.
3. 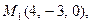
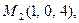
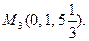 4.
4. 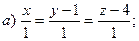
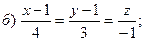
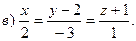
5. 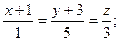
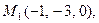
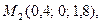
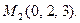 6.
6. 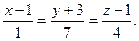 7.
7. 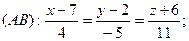
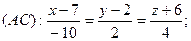
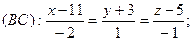
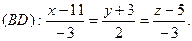 8.
8. 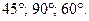
9. 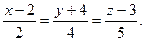 10.
10. 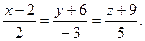
11. 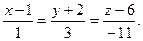 12.
12. 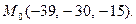 13.
13.