Численное интегрирование обыкновенных дифференциальных уравнений первого порядка

Постановка задачи

Многие практические задачи при их математическом моделировании сводятся к решению обыкновенных дифференциальных уравнений, т. е. к уравнениям, в которые входят независимая переменная, искомая функция и ее производные. В данной лабораторной работе рассматриваются численные методы поиска решения 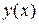для дифференциального уравнения первого порядка

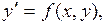(4.1)

которое удовлетворяет начальному условию

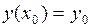. (4.2)

Известно [1]–[3], что для существования и единственности решения этой задачи(задача Коши) достаточно, чтобы функция 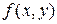и ее частная производная 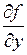были непрерывны в некоторой области плоскости 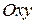, содержащей окрестность точки 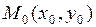. В то же время аналитическое решение задачи Коши можно найти только в отдельных, наиболее простых случаях, изучаемых в курсе высшей математики [1]. В остальных случаях решение ищется приближенными методами.

Все приближенные методы в зависимости от формы, в которой они представляют решение, можно условно разделить на следующие группы: аналитические (дают приближение 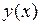аналитическим выражением), графические (дают приближение 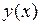графиком) и численные (дают приближение 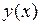с помощью таблицы). В данной лабораторной работе рассматриваются лишь два из большого числа численных методов решения задачи Коши: метод Эйлера и метод Рунге-Кутта [1]–[3]. При этом решение 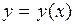находится в виде таблицы своих значений: 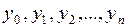соответственно для значений аргумента: .

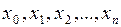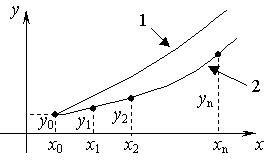
Рис. 4.1. Интегральная кривая y=y(x) (кривая 1) и

график приближенного решения задачи Коши (кривая 2)

Если соединить найденные в процессе решения точки 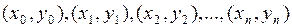, гладкой кривой, то получим график приближенного решения задачи Коши (рис. 4.1). Этот график по мере удаления от начальной точки 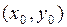все более и более будет отклоняться от графика точного решения (интегральная кривая). Степень отклонения приближенного решения от точного характеризует точность численного метода.

Метод Эйлера

Метод Эйлера состоит в следующем. Отрезок 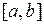, на котором ищется приближенное решение, делится точками

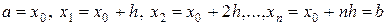
на n равных частей, где 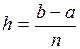– шаг интегрирования дифференциального уравнения. Зная значение 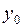решения 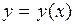в точке 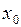, можно найти приближенно 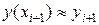в точках 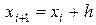по следующей рекуррентной формуле:

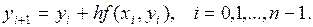(4.3)

Геометрически в методе Эйлера искомую интегральную кривую на интервале 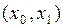заменяем отрезком касательной к этой интегральной кривой в точке 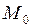(рис. 4.2). Уравнение касательной имеет вид

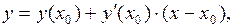
где 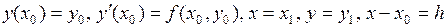. Поэтому ордината касательной в точке 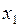равна 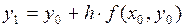, т. е. получили формулу (4.3) для случая 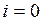. Далее строим касательную в точке 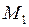к интегральной кривой 2, которая уже не совпадает с искомой. Находим ординату 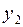касательной в точке 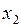, получаем формулу (4.3) уже при 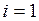. И так до тех пор, пока не достигнем конца отрезка b (рис. 4.3).

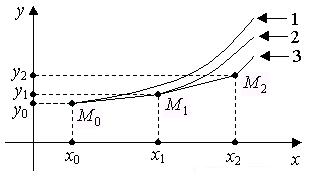
Рис. 4.2. Графическая иллюстрация метода Эйлера

1 – искомая интегральная кривая, 2,3 – другие интегральные кривые

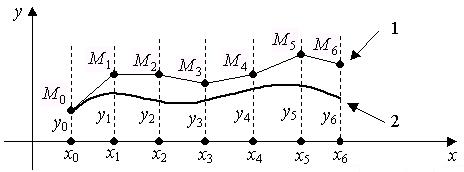
Рис. 4.3. Графическая иллюстрация метода Эйлера

1 – ломаная Эйлера, 2 – искомая интегральная кривая

Для оценки локальной погрешности метода Эйлера в точке 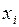используется неравенство [1]–[3]

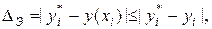(4.4)

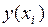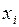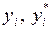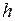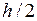где – точное значение решения задачи Коши в точке , а – приближенные значения решения, вычисленные по формуле (4.3) с шагами и соответственно. Из неравенства (4.4) следует, что для достижения необходимой точности 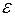нужно просчитать значение 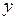по формуле (4.3) с шагом 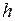, а затем, уменьшив шаг вдвое, снова повторить расчеты. Если при этом окажется, что для всех 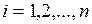выполняется неравенство: 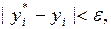то на шаге 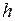достигнута необходимая точность.

Метод Рунге-Кутта

Метод Эйлера прост в реализации, но обладает сравнительно небольшой точностью. Поэтому для решения задачи Коши с повышенной точностью обычно используют метод Рунге-Кутта [1]–[3].

Как и прежде, разбиваем отрезок интегрирования 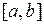на n равных частей. Зная значения 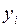– решение задачи Коши в точке 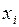, будем искать значение решения в точке 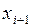по следующей формуле Рунге-Кутта:

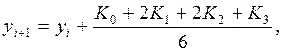(4.5)

где

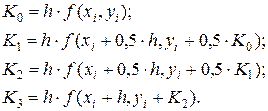(4.6)

Вычисления по формулам (4.5), (4.6) выполняются в следующем порядке. Для начальной точки 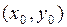, где 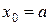, вычисляют 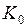, затем последовательно 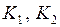и 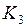. После этого все значения подставляются в формулу (4.5) 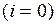и находится 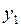при 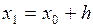. Далее процесс продолжается аналогично до конца отрезка .

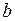Для оценки локальной погрешности метода Рунге-Кутта используется уже неравенство [2], [3]:

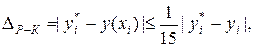(4.7)

где 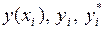имеют тот же смысл, что и в неравенстве (4.4).