Статического момента площади

Среди геометрических характеристик плоских сечений отрицательные значения может принимать:

Центробежный момент инерции

Координаты центра тяжести сечения определяются по формуле:

+ : z=S1/A, y=S1/A

Удельная потенциальная энергия упругой деформации вычисляется по формуле:

+ : u=..1E1+..2E2+..3E3 / 2

Первая классическая теория прочности имеет вид:

Lt;..

Вторая классическая теория прочности имеет вид:

V(..2-..3)<..

Третья классическая теория прочности имеет вид:

Lt;..

Четвёртая теория прочности имеет вид:

+ : корень из ½ (…)<…

Касательное напряжение не:

Вызывают изменение объёма нагруженного твёрдого тела

В случае объёмного напряженного состояния максимальные касательные напряжения в точках нагруженного объекта можно определить как:

+ : ..-.. / 2

Главная относительная линейная деформация это…

Деформация в направлении главного напряжения

Обобщенный закон Гука это…

Самый большой ответ

Действие угловых напряжений показано на рисунке:

+ : 4

Формула для определения угла закручивания в произвольном сечении стержня с круглым сечением при ф=0, постоянном крутящем моменте Т и постоянной жесткости GJp имеет вид:

+ : ф(х)= Tx/GJр

Формула для определения угла закручивания стержня с круглым сечением, накапливаемого на отдельном участке при 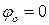, постоянном крутящем моменте Т и постоянной жесткости 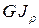имеет вид:

+ : ф(х)= Tl/GJр

При кручении в поперечных сечениях вала из шести внутренних силовых факторов отличен от нуля:

Крутящий момент Т

Формула для вычисления касательных напряжений, возникающих в поперечных сечениях стержня с круглым сечением при кручении имеет вид:

Тр/Ip

Модуль упругости материала является:

Мерой жесткости материала

Предел текучести материала это

Напряжение, при достижении которого деформация увеличивается без увеличения напряжения

Предел упругости материала представляет:

Максимальное напряжение, при превышении которого материал получает необратимую деформацию

В данном случае относительная продольная деформация в точках стержня определяется согласно формуле:

+ : E(x)=-N(x)/EA

Осевой момент инерции сечения относительно оси у вычисляются по формуле:

+ : Jy = интеграл z2*dA

Полярный момент инерции сечения относительно точки О вычисляются по формуле:

+ : Jp = интеграл p2*dA

Центробежный момент инерции сечения относительно осей у и z вычисляется по формуле:

+ : Jyz = интеграл y*z*dA

Чугун и сталь – материалы...

Изотропные

В сечении 1-1имеют место внутренние силовые факторы: