Розглянемо ряд з додатними членами

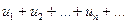( 1 )

Якщо існує границя 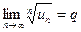, то

1) ряд ( 1 ) збігається, якщо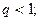

2) ряд ( 1 ) розбігається, якщо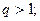

3) якщо 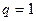, то питання про збіжність ряду ( 1 ) залишається відкритим ( треба використати інші ознаки ).

Приклади: Дослідити ряди на збіжність.

1.

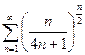
Розв’язання.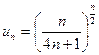

Знаходимо: 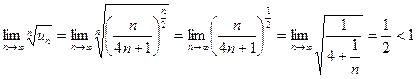, отже, ряд збіжний.

2.

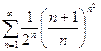
Розв’язання.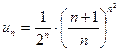

Знаходимо: ,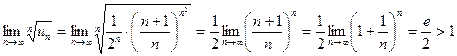

тому що 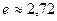, отже, ряд є розбіжним.

Інтегральна ознака Коші

Нехай члени ряду 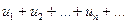( 1 )

додатні і не зростають, тобто 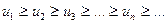, і існує така неперервна функція 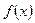, що .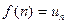

Тоді:

1) якщо невластивий інтеграл 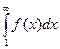збігається, то збігається і ряд ( 1 );

2) якщо інтеграл 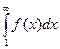розбігається, то і ряд ( 1 ) є розбіжним.

Приклад. Дослідити на збіжність ряд Діріхле: .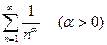

Розв’язання. Розглянемо функцію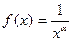

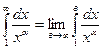
а) Нехай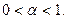

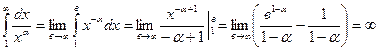, тому що ,

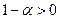отже ряд є розбіжним.

б) Нехай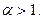

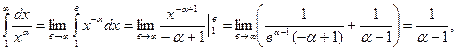
тому що 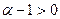, у цьому випадку ряд збігається.

в) Нехай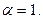

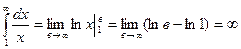, ряд розбігається.

Отже, ряд 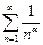збігається, якщо 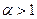і розбігається, якщо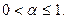

Приклади. Дослідити ряди на збіжність за допомогою інтегральної

ознаки Коші.

1)

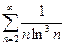
Розвязання. Складемо функцію 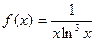і інтеграл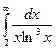

( нижня межа інтегрування є найменшим значенням n ).

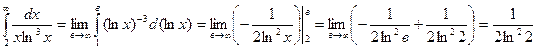
Інтеграл збігається, отже, і ряд є збіжним.

2)

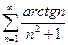
Розв’язання. 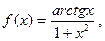досліджуємо інтеграл 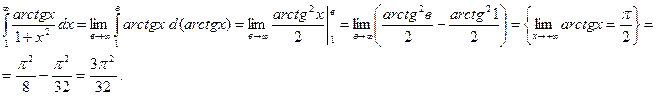Отже ряд збігається.

3)

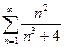
Розв’язання. 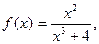досліджуємо інтеграл:

.

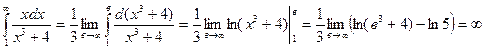Інтеграл розбігається, отже, і ряд є розбіжним.

Завдання для самостійної роботи

Дослідити ряди на збіжність за допомогою інтегральної ознаки Коші.

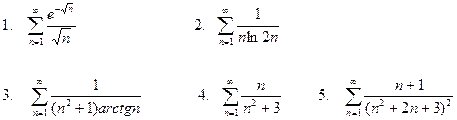
Знакопереміжні ряди

Ознака Лейбниця

Знакозмінним називається такий числовий ряд, серед членів якого є як додатні, так і від’ємні.

Частковим випадком знакозмінних рядів є знакопереміжні ряди, тобто такі ряди, в яких знаки членів строго чергуються, або ряди вигляду:

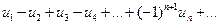( 1 )

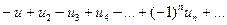( 2 ), де

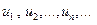- додатні числа.

Теорема Лейбниця. Якщо у знакопереміжному ряді ( 1 ) члени ряду спадають 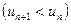і 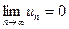, то ряд ( 1 ) є збіжним, його сума S додатна і .

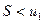Окрім знакопереміжного ряду ( 1 ) можна також розглядати ряд з модулів його членів

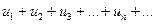( 3 )

Якщо ряд ( 3 ) збіжний, то ряд ( 1 ) також є збіжним.

Збіжність знакопереміжного ряду називається абсолютною , якщо збігається також ряд ( 3 ) з модулів його членів. Якщо ряд ( 1 ) збігається, але ряд ( 3 ) розбігається, то збіжність знакопереміжного ряду називається умовною.

Приклади. Дослідити ряди на абсолютну або умовну збіжність.

1.

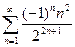
Розв’язання. Складемо ряд з модулів 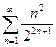, досліджуємо його за ознакою Даламбера.

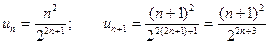
Знаходимо: .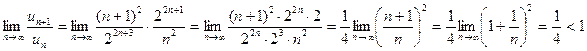

отже, ряд з модулів збігається, а це означає, що даний знакопереміжний ряд збігається абсолютно.

2.

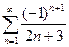
Розв’язання. Ряд з модулів 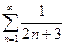досліджуємо за ознакою порівняння.

Ряд порівняння 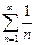- гармонічний ряд, який є розбіжним.

Знаходимо: 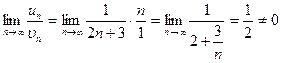, отже, ряд з модулів розбігається.

За ознакою Лейбниця 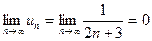, а це означає, що знакопереміжний ряд збігається умовно.

Завдання для самостійної роботи

Дослідити ряди на абсолютну або умовну збіжність.

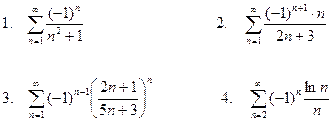
Література:[ 1 ], гл. XVI, § 1, 2, 3, 4, 5, 6, 7

[ 2 ], гл. ІІІ, § 1.

ТДАТУ

Кафедра вищої математики