Дифференциальные уравнения. 14. Дифференциальные уравнения первого порядка.
14. Дифференциальные уравнения первого порядка.
14.1. Обыкновенное дифференциальное уравнение, решение, общее решение, частное решение. Задача Коши.
14.2. Дифференциальное уравнение первого порядка с разделяющимися переменными.
14.3. Линейные дифференциальные уравнения первого порядка.
14.4. Дифференциальные уравнения первого порядка, сводящиеся к линейным.
15. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.
15.1. Однородные и неоднородные уравнения.
15.2. Свойства решений однородного уравнения.
15.3. Общее решение однородного уравнения.
15.4. Теорема о структуре общего решения неоднородного уравнения.
15.5. Подбор частного решения неоднородного уравнения для некоторых типов правых частей уравнения.
Список рекомендуемой литературы
1.Кремер Н.Ш. Высшая математика для экономических специальностей. М.: Высшее образование, 2007.
2.Просветов Г.И. Математика в экономике. Задачи и решения. М.: «Экзамен»,2008.
3.Карасев А.И., Аксютина З.М., Савельева Т.М. Курс высшей математики для экономических вузов. М.: Высшая школа, 1982.4.1 и 2.
4.Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, 1975.
5.Минорский В.П. Сборник задач по высшей математике.- М.: Наука. Главная редакция физико-математической литературы, 1977.
6.Пискунов Н.С. Дифференциальное и интегральное исчисления. Том I: учебник для студентов высших технических учебных заведений. Изд. 10-е, - М.: Наука. Главная редакция физико-математической литературы, 1978.
7.Пискунов Н.С. Дифференциальное и интегральное исчисления. Том 2: учебник для студентов высших технических учебных заведений. Изд. 13-е.- М.: Наука. Главная редакция физико-математической литературы, 1985.
8.Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. Том 1,2: Учеб. пособие для втузов. Изд, 2-е, перераб. и доп. - М.: Высшая школа.1978.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Задание 1. Найти пределы функций:
1. 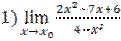 , при а)
, при а)  =1, б)
=1, б)  =2, в)
=2, в)  =∞;
=∞;
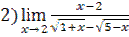 ;
; 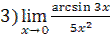 ;
; 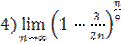 .
.
2. 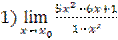 , при а)
, при а)  =2, б)
=2, б)  =1, в)
=1, в)  =∞;
=∞;
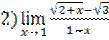 ;
; 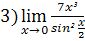 ;
; 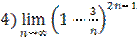 .
.
3. 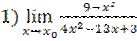 , при а)
, при а)  =1, б)
=1, б)  =3, в)
=3, в)  =∞;
=∞;
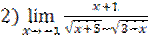 ;
; 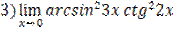 ;
; 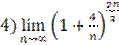 .
.
4. 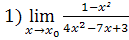 , при а)
, при а)  =2, б)
=2, б)  =1, в)
=1, в)  =∞;
=∞;
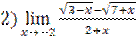 ;
; 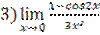 ;
; 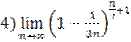 .
.
5. 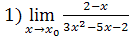 , при а)
, при а)  =1, б)
=1, б)  =2, в)
=2, в)  =∞;
=∞;
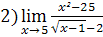 ;
; 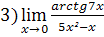 ;
; 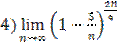 .
.
6. 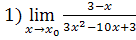 ; при а)
; при а)  =1, б)
=1, б)  =3, в)
=3, в)  =∞;
=∞;
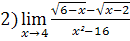 ;
; 
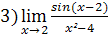 ;
; 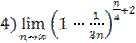 .
.
7. 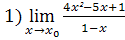 , при а)
, при а)  =
= 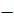 1, б)
1, б)  =1, в)
=1, в)  =∞;
=∞;
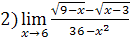 ;
; 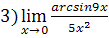 ;
; 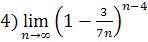
8. 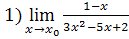 , при а)
, при а)  =2, б)
=2, б)  =1, в)
=1, в)  =∞;
=∞;
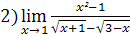 ;
; 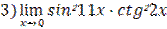 ;
; 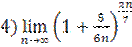 .
.
9. 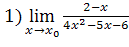 , при а)
, при а)  =
= 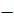 1, б)
1, б)  =2, в)
=2, в)  =∞;
=∞;
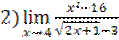 ;
; 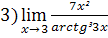 ;
; 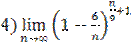 .
.
10. 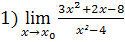 , при а)
, при а)  =
= 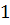 , б)
, б)  =
= 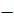 2, в)
2, в)  =∞;
=∞;
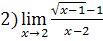 ;
; 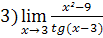 ;
; 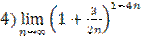 .
.
Задание 2. Найти производные:
11. , , .
12. , , .
13. , , .
14. , , .
15. , , .
16. , , .
17. , , .
18. , , .
19. , , .
20. , , .
Задание 3. Найти полный дифференциал функции 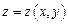 :
:
21.z = 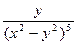 . . | 22.z = 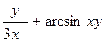 . . |
| 23.z =ln(x2+y2+2x+1). | 24.z =exy . |
25.z = 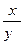 . . | 26.z =xy . |
| 27.z =xex . | 28.z =sin(x+3y). |
| 29.z =ln(x+e-y). | 30.z =cosy+(y–x)siny. |
Задание 4. Исследовать функцию 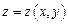 на экстремум:
на экстремум:
| 31.z =x2+2xy+2y2+4y | 32.z =-x2 +xy-y2+2x-y+3 |
| 33.z =-x3-xy+y2+3x+6y+3 | 34.z =-3x3+y2+x+3y+2 |
35.z =-x2- 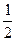 y2-xy-x+y+1 y2-xy-x+y+1 | 36.z =2x3-6y2-6x+2y+4 |
37.z = 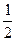 x2+2y2-xy+2x- x2+2y2-xy+2x- 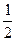 y+7 y+7 | 38.z = 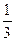 x3-y2-x+ x3-y2-x+ 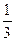 y y |
| 39.z =x2-y2-xy–x-y+3 | 40.z =x3+y3–3xy |
Задание 5. Найти неопределенные интегралы и результаты
проверить дифференцированием:
41.а) 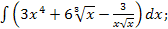 б)
б) 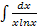 ; в)
; в) 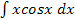 ; г)
; г) 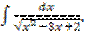
42.а) 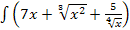 dx; б)
dx; б) 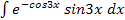 ; в)
; в) 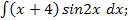 г)
г) 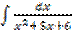
43.а) 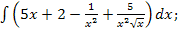 б)
б) 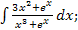 в)
в) 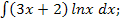 г)
г) 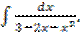
44.а) 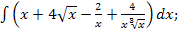 б)
б) 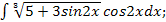 в)
в) 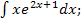 г)
г) 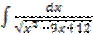
45.а) 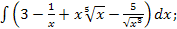 б)
б) 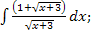 в)
в) 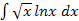 ; г)
; г) 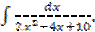
46.а) 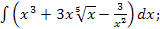 б)
б) 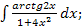 в)
в) 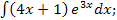 г)
г) 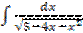
47.а) 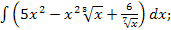 б)
б) 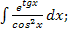 в)
в) 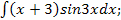 г)
г) 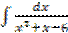
48.а) 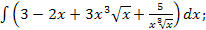 б)
б) 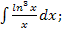 в)
в) 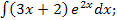 г)
г) 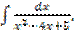
49.а) 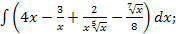 б)
б) 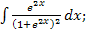 в)
в) 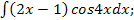 г)
г) 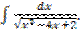
50.а) 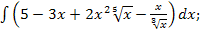 б)
б) 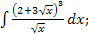 в)
в)  г)
г) 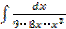
Задание 6. Вычислить площадь фигуры, ограниченной данными линиями (сделать чертеж):
51. 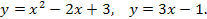
52. 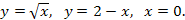
53. 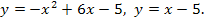
54. 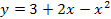 ,
, 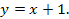
55. 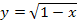 ,
, 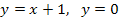 .
.
56. 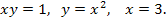
57. 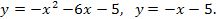
58. 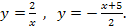
59. 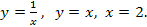
60. 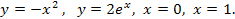
Задание 7. Найти общее решение дифференциального уравнения 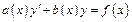 и частное решение, удовлетворяющее начальному условию
и частное решение, удовлетворяющее начальному условию 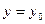 ,
, 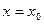 :
:
61. 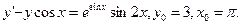
62. 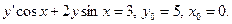
63. 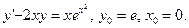
64. 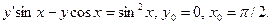
65. 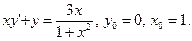
66. 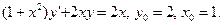
67. 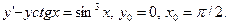
68. 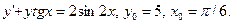
69. 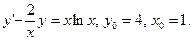
70. 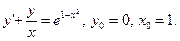
Задание 8. Найти общее решение дифференциального уравнения:
71. 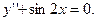
72. 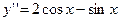 .
.
73. 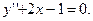
74. 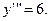
75. 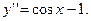
76. 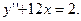
77. 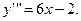
78. 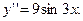
79. 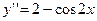 .
.
80. 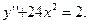
Задание 9. Написать три первых числа степенного ряда по заданному высшему члену . Найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала. Написать три первых члена степенного ряда по заданному общему члену: Найти область сходимости степенного ряда.
81. 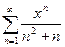 . . | 82. 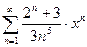 |
83. 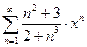 | 84. 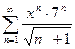 |
85. 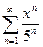 | 86. 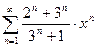 |
87. 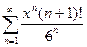 | 88. 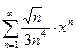 |
89. 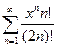 | 90. 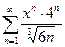 |
