Геометрическое истолкование процесса

Мы начинаем искать решение от начала координат (0;0). Так как при вычислении х мы должны сохранять неизменным у, то геометрически это соответствует движению по горизонтали до пересечения с прямой, соответствующей 1-ому уравнению. Затем, сохраняя неизменным найденной значение х, движемся по вертикали, пока не пересечем прямую, соответствующую 2-ому уравнению. На рисунке такому процессу соответствует путь ОАВ. На этом заканчивается одна итерация. Дальнейшие итерации производятся точно таким же образом. Процесс сходится к решению системы уравнений.

Посмотрим, что случится, если мы переставим уравнения.

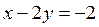
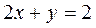
Решение системы не изменилось, но диагональные коэффициенты по модулю стали меньше недиагональных. При этом получим:

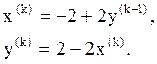
Результаты последовательных итераций составят:

Итерация	х	у
	-2
		-18
	-33

Из таблицы видно, что итерационный процесс с каждой новой итерацией удаляет нас от решения системы, то есть итерационный процесс расходится. В отличие от первого случая, мы здесь начинаем движение от начала координат по оси х в противоположном направлении, т.е. к графику второго уравнения системы (2.9).

Рассмотрим еще один вариант системы, в которой один из диагональных коэффициентов по модулю больше, а другой – меньше недиагонального коэффициента.

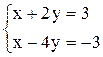(2.10)

Решением системы является х = 1, у = 1. При этом получим:

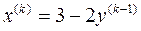
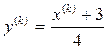
Результаты последовательных итераций составят:

Итерация	х	у
		3/2
		3/4
	3/2	9/8
	3/4	15/16

Видно, что итерационный процесс сходится к решению системы.

Таким образом, выполнение для системы из двух уравнений условия, при котором диагональные коэффициенты по модулю больше недиагональных, гарантирует сходимость метода, но в то же время существуют системы, для которых эти условия не выполняются, но метод итераций все равно сходится. Поэтому указанные условия для системы являются достаточными условиями для сходимости, но не являются необходимыми.

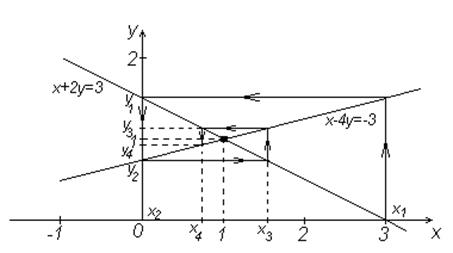Рисунок 1.6 – Итерационный процесс решения системы (2.10)

В обоих рассмотренных случаях сходимость (или расходимость) носит колебательный характер, то есть итерационный процесс развивается по спирали. Однако, в зависимости от уравнений системы, итерационный процесс может сходиться к решению системы с одной стороны.

Приведем без доказательства достаточные условия сходимости итерационного метода Гаусса-Зейделя для системы (2.8) из n уравнений с n неизвестными.

Введем определение: система уравнений называется неприводимой, если нельзя вычислить какие-либо неизвестные, решая меньше чем n уравнений.

Если система уравнений неприводима, и если для всех i выполняется:

,

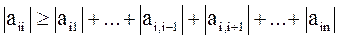и если по крайней мере для одного i выполняется

,

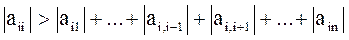то итерационный метод Гаусса-Зейделя сходится к решению системы уравнений (2.8).