Функция распределения вероятностей

Тема 6. Случайные величины

Наряду со случайными событиями одним из основных понятий теории вероятностей является понятие случайной величины.

Случайной величиной называется величина, принимающая в результате испытания некоторое, наперед неизвестное значение, которое может изменяться от испытания к испытанию. Случайные величины принято обозначать 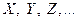, их возможные значения -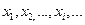

Случайные величины могут классифицироваться следующим образом:

· Величины количественные и качественные. Количественные величины называются также числовыми.

· Величины одномерные и многомерные.

· Величины дискретные и непрерывные (для числовых величин).

Дискретная случайная величина. Закон распределения вероятностей дискретной случайной величины

Дискретной случайной величиной называется случайная величина, принимающая отдельные, изолированные друг от друга значения. Возможные значения дискретной случайной величины образуют конечное множество или счетное множество (бесконечное множество, элементы которого можно пронумеровать).

Например:

Для задания случайной величины недостаточно знать только ее возможные значения. Две случайные величины могут иметь одинаковые значения, но принимать их с различными вероятностями (например, оценки на экзамене у сильных и слабых студентов). Поэтому необходимо указать и возможные значения, и их вероятности.

Законом распределения дискретной случайной величины называется соответствие между возможными значениями это величины и их вероятностями.

Закон распределения может быть задан тремя способами:

1) Табличный способ – в первой строке таблице в порядке возрастания перечисляются возможные значения случайной величины, во второй – их вероятности.

В данной таблице p_i – вероятность того, что случайная величина X приняла значение x_i ( 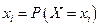), причем сумма вероятностей в нижней строке должна быть равна единице: 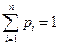(доказать самостоятельно). Такую таблицу называют рядом распределения вероятностей дискретной случайной величины.

2) Графический способ – по оси абсцисс откладываются возможные значения случайной величины, по оси ординат – их вероятности. Полученные точки соединяются отрезками. Такой график называют многоугольником распределения.

Аналитический способ – соответствие между значениями случайной величины и их вероятностями задается с помощью формулы: .

Функция распределения вероятностей

Непрерывной случайной величиной называется случайная величина, принимающая любое значение из некоторого конечного или бесконечного промежутка.

Например:

Количество значений непрерывной случайной величины бесконечно, невозможно перечислить все ее возможные значения, поэтому необходимы другие способы ее задания.

Распределение вероятностей непрерывной случайной величины может быть задано двумя способами: с помощью функции распределения вероятностей и с помощью плотности распределения вероятностей, причем функция распределения вероятностей является общим способом задания случайной величины, применимым как для дискретной случайной величины, так и для непрерывной.

Функцией распределения вероятностей случайной величины называется функция, равная в каждой точке х вероятности того, что случайная величина Х примет значение меньшее, чем х: .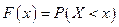

Свойства функции распределения вероятностей:

1) Поскольку функция распределения равно вероятности, ее значение находится в промежутке от 0 до 1: .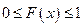

2) Функцией распределения вероятностей является неубывающей.

Доказательство:

3) Вероятность того, что случайная величина Х попадет в интервал [a; b), равна разности значений функции распределения в конце и в начале интервала: .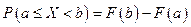

4) Если все значения случайной величины Х принадлежат отрезку [a; b], то значение функции распределения равно нулю при 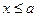и равно единице при х > b.

5) 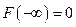и .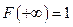

Доказательство:

6) Вероятность того, что непрерывная случайная величина примет конкретное значение a, равна нулю: .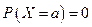

7) Для непрерывной случайной величины вероятности попадания в открытый, закрытый и полузакрытый числовые промежутки равны между собой: .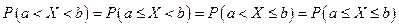

Графики функции распределения вероятностей имеют вид: