Интервальная оценка вероятности биноминального распределения по относительной частоте
Найдем доверительный интервал для оценки вероятности по относительной частоте, используя формулу:
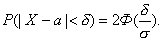
Если n достаточно велико и р не очень близка к нулю и единице, то можно считать, что относительная частота распределена приближенно по нормальному закону, причем М(W)= р. Заменив Х на относительную частоту , математическое ожидание - на вероятность, получим равенство:
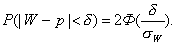
Приступим к построению доверительного интервала (р1, р2), который с надежностью покрывает оцениваемый параметр р Потребуем, чтобы с надежностью g выполнялось соотношение указанное выше равенство:
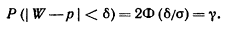
Заменив
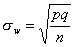 ,
,
получим:
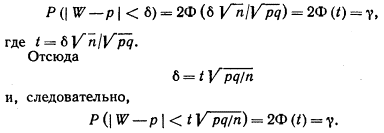
Таким образом, с надежностью g выполняется неравенство (чтобы получить рабочую формулу, случайную величину W заменим неслучайной наблюдаемой относительной частотой w и подставим 1- р вместо q):
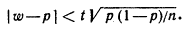
Учитывая, что вероятность р неизвестна, решим это неравенство относительно р. Допустим, что w > р. Тогда
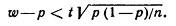
Обе части неравенства положительны; возведяих в квадрат, получим равносильное квадратное неравенство относительно р:
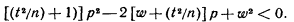
Дискриминант трехчлена положительный, поэтому корни действительные и различные:
меньший корень
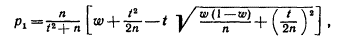
больший корень:
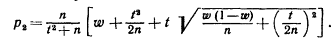
Замечание1: При больших значениях n , пренебрегая слагаемыми
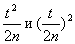 ,и
,и
учитывая
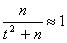
получим приближенные формулы для границ доверительного интервала :
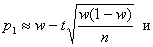
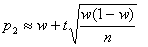
Пример1. Производят независимые испытания с одинаковой и неизвестной вероятностью появления события А в каждом испытании. Найти доверительный интервал для оценки вероятности с надежностью 0,95, если в 80 испытаниях событие А появилось 16 раз.
По условию n =80, m=16, =0,95. Относительная частота
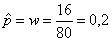 .
.
Из соотношения Ф(t)=0,95/2 = 0,475 по таблице находим t = 1,96. Т.к. n<100, то используем точные формулы, получим : р1= 0,128, р2= 0,299.
Замечание 2: Если n мало, то используем для определения концов доверительного интервала вероятности события при биноминальном распределении "Таблицу доверительных границ р1 и р2". Значения р1 и р2 находят в зависимости от n и m.
Пример. В пяти независимых испытаниях событие А произошло 3 раза. Найти с надежностью 0,95 интервальную оценку для вероятности события А в единичном испытании.
По условию задачи n=5, m=3. Имеет место схема повторных испытаний. Используя таблицу, находим доверительный интервал : 0,147<p<0,947.
Контрольные вопросы
1. Определение статистической оценки неизвестного параметра.
2. Какая оценка называется точечной?
3. Каким требованиям должны удовлетворять статистические оценки?
4. Сформулировать определения генеральной средней и генеральной дисперсии.
5. Записать выражения для вычисления выборочной средней, выборочной дисперсии и исправленной дисперсии. Какая из этих оценок не является несмещенной?
6. Методики вычисления границ доверительного интервала для оценки математического ожидания нормально распределенной СВ при известном и неизвестном .
7. Методика вычисления границ доверительного интервала для оценки среднего квадратического отклонения нормально распределенной СВ.
8. Доверительный интервал вероятности биноминального распределения по относительной частоте при больших n , при n<100.
