Интервальная оценка коэффициента корреляции

Для двумерного нормального распределения генеральной совокупности коэффициент корреляции не только решает вопрос о том, зависимы признаки или нет, но и измеряет степень их связи. Поэтому в «нормальном» случае нужно уметь не только проверять гипотезу H₀:r=0, но и указывать доверительные интервалы для истинного r. Особенно данная задача имеет смысл в случае значимого выборочного коэффициента корреляции. Для этого нужно знать закон распределения выборочного коэффициента корреляции r не только при r=0, но и при произвольном r.

В общем случае закон распределения r имеет довольно сложный вид (это т.н. r-распределение). Однако при больших n и малых по абсолютному значению r выборочный коэффициент корреляции можно считать распределенным нормально с математическим ожиданием r и дисперсией

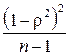. (4.29)

Но для указанной выше цели этот факт использовать довольно трудно в связи с тем, что неизвестное значение r входит в выражение не только среднего, но и дисперсии.

При достаточно больших выборках (n³50) выборочный коэффициент корреляции имеет приближенно нормальное распределение 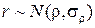, где

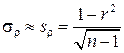. (4.30)

В этом случае доверительный интервал для r, будет иметь вид

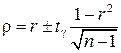, (4.31)

где t_g находится из уравнения 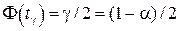, F(x) – функция Лапласа.

В случае небольшого объема выборки r-распределение существенно отличается от нормального. В этом случае можно использовать преобразование, предложенное Р. Фишером:

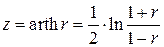, (4.32)

где 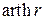– обратная функция гиперболического тангенса. Он показал, что величина z, определенная соотношением (4.32), уже при небольших n (n³10) с хорошим приближением следует нормальному распределению. При этом

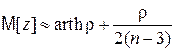, (4.33)

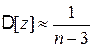. (4.34)

Это позволяет построить доверительный интервал 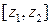для 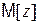по формуле

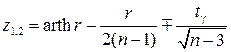. (4.35)

Откуда следует, что истинное значение коэффициента корреляции r c той же доверительной вероятностью g=1–a заключено в пределах

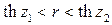. (4.36)

Здесь thz – это тангенс гиперболический от аргумента z, определяемый с помощью соотношения

.

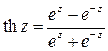Пример 4.4. По данным n=38 предприятий получен коэффициент корреляции r=–0,654, характеризующий тесноту связи между себестоимостью продукции (y) и производительностью труда (x). Построить интервальную оценку для r, задавшись 95%-й доверительной вероятностью.

Решение. Применяя z-преобразование Фишера для найденного коэффициента корреляции, получим

.

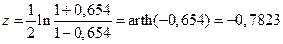Поскольку t_0,95=1,96, то

, .

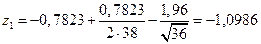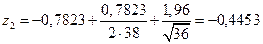Доверительный интервал для M(z) будет иметь вид

.

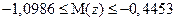Осуществляем обратное z-преобразование по формуле (4.45):

.

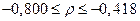Таким образом, можно утверждать, что с доверительной вероятностью g=0,95 истинное значение коэффициента корреляции r между себестоимостью продукции (y) и производительностью труда (x) будет лежать в интервале от –0,8 до –0,418. â

Замечание. Величина 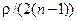в формуле (4.35) мала по сравнению с 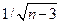. Поэтому ею обычно пренебрегают, когда речь идет об оценивании r по одной выборке. Но при соединении результатов, полученных по нескольким выборкам, это слагаемое все же может оказывать влияние.

Дополнение 1.
КОРРЕЛЯЦИОННОЕ ОТНОШЕНИЕ И ЕГО СВОЙСТВА

Если линии регрессии не являются прямыми, то коэффициент корреляции лишь с некоторым приближением может рассматриваться как показатель связи между случайными величинами X и Y. В случае нелинейной связи представляют интерес показатели, характеризующие концентрацию распределения (и, следовательно, тесноту связи) около линий регрессии. Таким показателем является корреляционное отношение, введенное К. Пирсоном.

Разброс значений случайной величины Y около математического ожидания m_y=M[Y] измеряется дисперсией

.

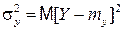Этот разброс может быть вызван двумя факторами: 1) влиянием корреляционной зависимости Y от X; 2) влиянием прочих (остаточных) факторов, не влияющих на X.

Влияние первого фактора измеряется величиной

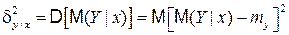, (4.37)

т.е. дисперсией линии регрессии относительно математического ожидания m_y.

Влияние второго фактора измеряется величиной

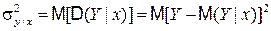, (4.38)

т.е. дисперсией Y относительно линии регрессии.

В соответствие со свойствами дисперсии можно записать, что

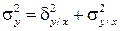. (4.39)

Корреляционным отношением Y на X называется отношение

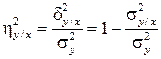. (4.40)

Аналогично определяется корреляционное отношение X на Y

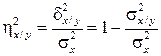. (4.41)

Рассмотрим теперь свойства корреляционного отношения.

1⁰. Корреляционное отношение всегда заключено между 0 и 1, т.е.

.

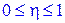2⁰. Корреляционное отношение равно 0, тогда и только тогда, когда отсутствует корреляционная зависимость.

Действительно, пусть 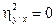. Тогда 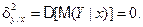Отсюда следует, что M[Y|x]=const, т.е. условное математическое ожидание "не реагирует" на изменения значений величины X (линия регрессии параллельна оси Oy). Это и означает, что корреляционная зависимость Y от X отсутствует. Справедливо и обратное утверждение, поскольку при отсутствии корреляционной зависимости M[Y|x]=const, поэтому D[M(Y|x)]=0 и h_y/x=0.

3⁰. Корреляционное отношение равно 1, тогда и только тогда, когда существует функциональная зависимость (y=f(x) и x=g(y)).

Действительно, пусть 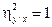. Тогда 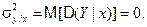Но так как дисперсия неотрицательна, то D[Y|x]=0 при любом значении x, а 'это означает, что величина Y принимает единственное значение при котором x, т.е. зависимость Y от X функциональная. Справедливо и обратное утверждение. Из данного свойства следует, что чем ближе корреляционное отношение к единице, тем «концентрация» значений Y к линии регрессии.

4⁰. Коэффициент корреляции не превосходит по абсолютной величине корреляционное отношение:

|r| £ h

Отметим, что между h_y/x и h_x/y нет какой-либо простой зависимости. Например, Y может быть не коррелированно с X и h_x/y=0, тогда как другой показатель может быть равен 1, т.е. h_y/x=1.

Таким образом, поскольку коэффициент корреляции можно рассматривать как меру линейности регрессии, то величину

h² – r²

можно рассматривать как меру нелинейности регрессии, т.е. отклонения линии регрессии от прямой.

5⁰. Выполнение равенства h_y/x=|r_xy| является необходимым и достаточным условием того, чтобы регрессия Y на X была точно линейной. Аналогично и для h_x/y.

Для того чтобы оценить корреляционное отношение исходные нужно сгруппировать в виде корреляционной таблицы. В каждой клетке этой таблицы приводятся численности n_ij тех пар (x,y), компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждой из переменных) равными между собой, выбирают центры x_i (соответственно y_i) этих интервалов и числа n_ij в качестве основы для расчетов. Точечной оценкой корреляционных отношений являются выражения:

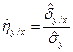и 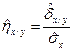(4.42)

где 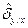и 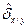– средние квадратичные отклонения условных средних от общей средней:

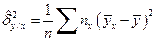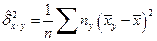, . (4.43)

Отметим, что корреляционное отношение не меняется при переходе к новым переменным (4.26), т.е.

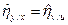и .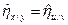

Выше мы уже отмечали, что величину h² – r² можно рассматривать как меру нелинейности регрессии, т.е. отклонения линии регрессии от прямой. Поэтому величины

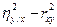и 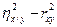(4.44)

можно рассматривать как меру нелинейности корреляционной зависимости. Если величины (4.44) значимо отличаются от нуля, то имеется нелинейная корреляционная зависимость, если не значимо, то имеющиеся данные не противоречат гипотезе о наличии линейной корреляционной зависимости.

Дополнение 2.
РАНГОВАЯ КОРРЕЛЯЦИЯ

В анализе социально-экономических явлений часто встречаются с признаками, не поддающимися количественной оценке. Например, требуется оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле, что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако, этот способ лишен объективности, т.к. разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Ранжирование – это процедура упорядочения объектов изучения, которая выполняется на основе предпочтения. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Ранг – это порядковый номер значений признака, расположенных в порядке возрастания или убывания. Переменные, значениями которым являются ранги значений соответствующих признаком, называются порядковыми (или ординарными). Корреляция между рангами, точнее между порядковыми переменными, более точно отражает соотношение между способностями учащихся, чем корреляция между отметками. Система понятий и методов, позволяющих измерять и анализировать статистическую связь между порядковыми переменными, называется анализом ранговых корреляций. Методы ранговой корреляции широко используются, в частности, при организации и статистической обработке различного рода систем экспертных оценок.

Исследователь обращается к порядковым переменным в ситуациях, когда шкала непосредственного количественного измерения степени проявления этого свойства в объекте неизвестна (в том числе по причине объективного отсутствия такой). Например, в ситуации, когда исследуется качество жилищных условий можно рассмотреть четыре категории качества: «плохое», «удовлетворительное», «хорошее», «очень хорошее». Приписав каждой из обследованных семей одну из категорий, мы тем самым получаем возможность упорядочить (ранжировать) обследуемые семьи по этому свойству и ввести порядковую переменную.

Порядковые переменные вводят также и в том случае, шкала непосредственного количественного измерения признака имеет условный смысл и интересует нас только как вспомогательное свойство для последующего ранжирования рассматриваемых объектов.

При упорядочении объектов по какому-либо свойству могут встретиться ситуации, когда два объекта или целая группа их оказываются неразличимыми с точки зрения проявления в них этого свойства. Тогда каждому из объектов однородной группы приписывается ранг, равный среднему арифметическому значению тех мест, которые они занимают, а полученные таким образом ранги называются «связными» (или «объединенными»).

Пример 4.5. Проранжировать предприятия автомобильной промышленности одного из регионов по величине балансовой прибыли

Таблица 4.7

№ предприятия	Балансовая прибыль, млн руб	Ранжирование (ранги)
		6,5
		6,5

Решение. Наиболее предпочтительную предприятию, величина балансовой прибыли которого наибольшая, присваивается ранг «1»; затем в порядке уменьшения величины балансовой прибыли были проранжированы все рассматриваемые предприятия автомобильной промышленности. Для данного примера характерно наличие связных рангов.

Принцип нумерации значений исследуемых признаков является основой непараметрических методов изучения взаимосвязи между социально-экономическими явлениями и процессами. Среди непараметрических методов оценки наибольшее значение имеют ранговые коэффициенты Спирмена и Кендалла. Эти коэффициенты могут быть использованы для определения тесны связей как между количественными, так и между качественными признаками при условии, если их значения упорядочить или проранжировать по степени убывания или возрастания признака.