Нахождение амплитудного и фазового спектров входного сигнала
Амплитудный спектр входного сигнала есть модуль спектральной плотности. Согласно этому можно записать аналитическое выражение амплитудного спектра входного сигнала:
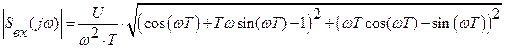(2.2.1)
Амплитудный спектр сигнала – функция чётная, поэтому будем рассматривать график только в области положительных частот.
График амплитудного спектра представлен на рис. 2.2
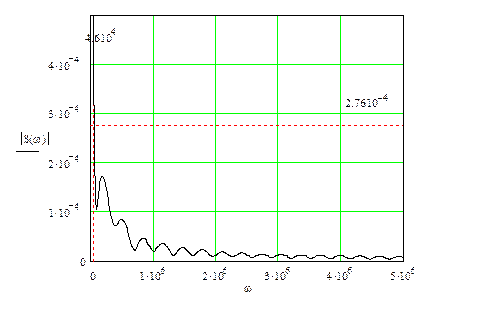
Рис 2.2 Амплитудный спектр входного сигнала
Ширина спектра:
Согласно амплитудному методу определения ширины спектра Dw на уровне 0.1×|S(w)| (рис. 2.2):
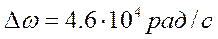
Фазовый спектр:
Вычислить фазовый спектр можно по формуле:
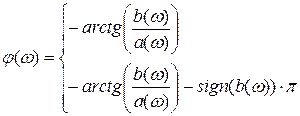, где (2.2.2)
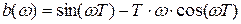
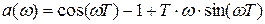
Эту же задачу можно решить с помощью MathCAD, используя функцию arg.
График фазового спектра представлен на рис. 2.3
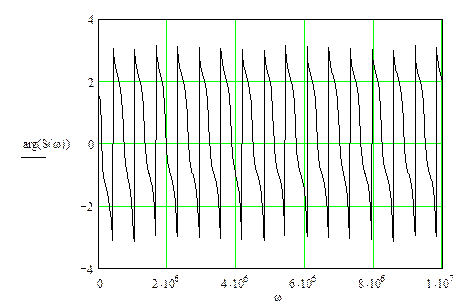
Рис 2.3 Фазовый спектр входного сигнала
Частотный анализ.
Нахождение частотного коэффициента передачи цепи
Анализ начнём с поиска коэффициента передачи цепи в операторной форме К(р).
Для этого обратимся к исходной схеме заданной цепи, представленной на рис 3.1.
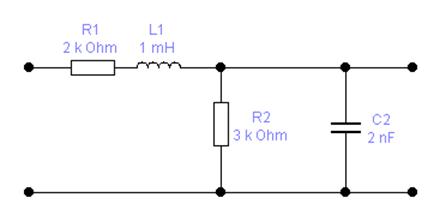
рис 3.1 Исходная схема цепи .
Представим все элементы цепи в операторной форме.
; 
; 
; 
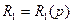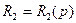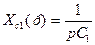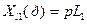, (3.1)
где p=jw-оператор Лапласа.
Зарисуем исходную схему в операторной форме:
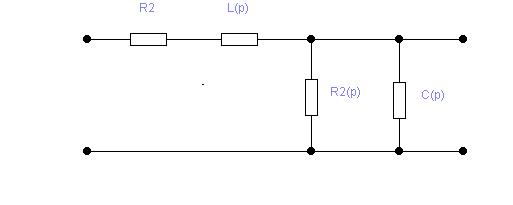
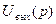
рис 3.2 Исходная схема цепи в операторной форме.
Для коэффициента передачи можно записать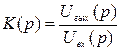 
(3.2)
Подставляем (3.1) в формулу коэффициента передачи (3.2), получаем:
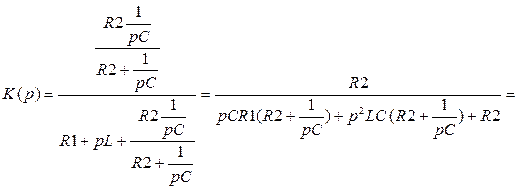
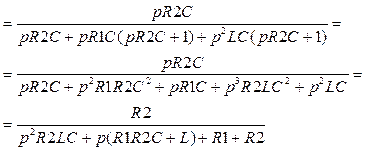(3.3)
Произведем замену в формуле (3.3):
; 
; 
; 
; 
; 
; 
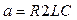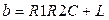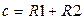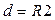
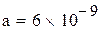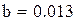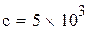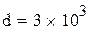(3.4)
Получаем:
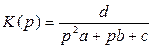(3.5)
Теперь для того, чтобы перейти к комплексному коэффициенту передачи необходимо в формуле (3.5) оператор р заменить на jw.Получаем:
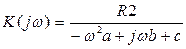(3.6)
Подставляем значения (3.4) и получаем:
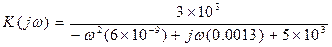(3.7)
Исходя из формулы (3.7) можно определить амплитудночастотную (АЧХ) и фазочастотную (ФЧХ) характеристику цепи.
Модуль коэффициента передачи является аналитическим выражением для АЧХ заданной цепи, запишем его:
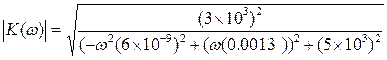(3.8)
С помощью программы Mathcad построим график выражения (3.8):
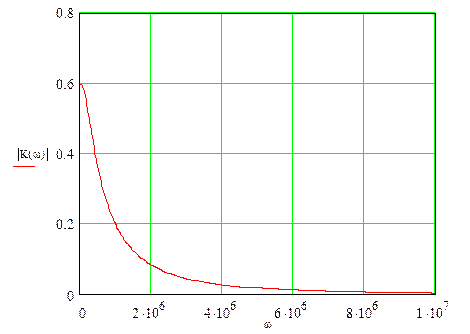
рис 3.3 График АЧХ для заданной цепи.
ФЧХ цепи является разность фаз выходного и входного напряжения. В формуле (3.7) фазу выходного напряжения будет определять числитель, а входного- знаменатель
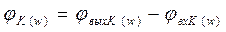
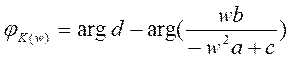(3.9)
С помощью программы Mathcad построим график выражения (3.9):
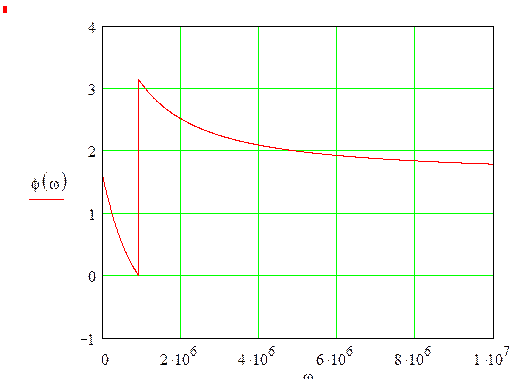
рис 3.4 График ФЧХ для заданной цепи
Целью частотного анализа является получение двух важных характеристик: амплитудно-частотной характеристики (АЧХ - зависимость модуля комплексного выражения тока контура от частотывходного сигнала) и фазочастотной характеристики (ФЧХ - зависимость фазы от частоты входного сигнала). Для получения этих характеристик достаточно найти частотный коэффициент передачи цепи. Его модуль определяет АЧХ цепи, а аргумент – ФЧХ.
Переходная и импульсная характеристики цепи.