Нерастворимы, так что они образуют одну паровую (п) и две жидких (ж1 и ж2) фазы
В двухкомпонентных системах.
Введение.
5.1.1. Общее определение диаграмм Т–N 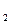 двухкомпонентных систем.
двухкомпонентных систем.
Под диаграммой Т–N 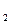 двухкомпонентной системы понимают изобарическое сечение (р–const) диаграммы Т– р –N
двухкомпонентной системы понимают изобарическое сечение (р–const) диаграммы Т– р –N 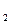 данной системы.
данной системы.
Такое сечение может охватывать несколько фазовых равновесий с участием двух, трех и четырех фаз, поскольку ω = 4–А и А≤4. Условие р–const означает, что р – свободная переменная с заданным значением.
Мы ограничимся рассмотрением лишь двухфазных равновесий (А=2, ω = 4-2= 2), но при необходимости будем привлекать трехфазные равновесия (А=3, ω = 4-3=1). Кроме того, мы будем учитывать возможность появления в двухфазных двухкомпонентных системах особых условий равновесия, снижающих вариантность системы (при L>0 и А=2 получаем ω = 4 – А –L = 4- 2- L = 2–L).
5.1.2. Содержание диаграмм Т–N 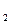 при двухфазных равновесиях
при двухфазных равновесиях
В двухкомпонентных системах.
Пусть мы имеем дело с равновесием двух фаз ε и λ (А=2) в двухкомпонентной системе (К= 2) без химических реакций (R=0) и без особых условий равновесия (L=0). Тогда
а = 2 + (К-1)А = 2+(2-1)2 = 4
{Т, р, {N 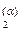 }} = {Т, р, N
}} = {Т, р, N 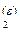 N
N 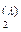 }
}
ω = 2+К–А –R–L = 2+2-2-0-0 = 2
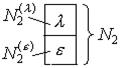
 Т, р – свободные переменные
Т, р – свободные переменные
N 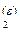 = N
= N 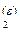 (Т, р) – уравнение поверхности S
(Т, р) – уравнение поверхности S 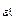 для фазы ε,
для фазы ε,
N 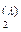 = N
= N 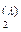 (Т, р) – уравнение поверхности S
(Т, р) – уравнение поверхности S 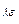 для фазы λ.
для фазы λ.
 р–const (изобарическое сечение)
р–const (изобарическое сечение)
 N
N 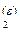 = N
= N 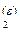 (Т) или Т = Т (N
(Т) или Т = Т (N 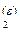 ) – уравнение линии L
) – уравнение линии L 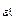 для фазы ε,
для фазы ε,
N 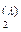 = N
= N 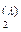 (Т) Т = Т (N
(Т) Т = Т (N 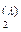 ) – уравнение линии L
) – уравнение линии L 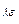 для фазы λ.
для фазы λ.
 Заключение
Заключение
Диаграмма Т–N 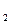 для равновесия двух фаз ε и λ в двухкомпонентной системе – графическое изображение зависимостей - линий Т (N
для равновесия двух фаз ε и λ в двухкомпонентной системе – графическое изображение зависимостей - линий Т (N 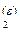 ) и Т (N
) и Т (N 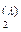 ) при заданном р.
) при заданном р.
Обе эти зависимости могут быть получены опытным путем в табличной форме и затем изображены графически. Их характерные виды для разных двухфазных равновесий рассмотрены ниже.
5.2. Равновесия жидкость – пар.
5.2.1. Компоненты 1 и 2 в паровом и жидком состояниях неограниченно взаимно
растворимы так, что они образуют одну паровую (п) и одну жидкую (ж) фазы.
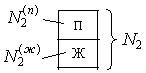 Зависимости
Зависимости 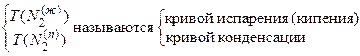 , они могут быть без внутренних экстремумов (рис.1) и с внутренними экстремумами (рис. 2. и 3).
, они могут быть без внутренних экстремумов (рис.1) и с внутренними экстремумами (рис. 2. и 3).
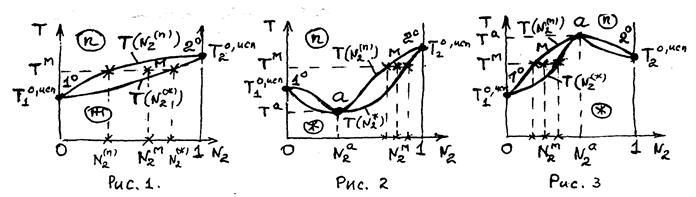
Граничные точки 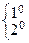 принадлежат одновременно
принадлежат одновременно 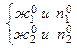 фазам, они характеризуют равновесия
фазам, они характеризуют равновесия 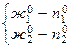 в чистых компонентах
в чистых компонентах 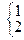 .
.
Внутренняя экстремальная точка а принадлежит ж. и п. фазам, где выполняется особое условие равновесия  (так что L=1 и ω = 4–А –L = 4-2-1 = 1), она называется азеотропной точкой (от греч. аzeotrope – кипящий без изменения). Точка М служит примером расчётной точки.
(так что L=1 и ω = 4–А –L = 4-2-1 = 1), она называется азеотропной точкой (от греч. аzeotrope – кипящий без изменения). Точка М служит примером расчётной точки.
Компоненты 1 и 2 в паровом состоянии неограниченно взаимно растворимы, но в
Жидком состоянии они либо ограниченно взаимно растворимы, либо полностью
нерастворимы, так что они образуют одну паровую (п) и две жидких (ж1 и ж2) фазы.
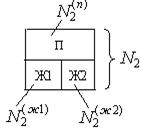 Для каждой из двух жидких фаз ж1 и ж2 имеется одна из двух кривых испарения Т (N
Для каждой из двух жидких фаз ж1 и ж2 имеется одна из двух кривых испарения Т (N 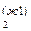 ) и Т (N
) и Т (N 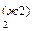 ), где эта фаза способна к равновесному сосуществованию с паровой фазой (рис.1 и 2).
), где эта фаза способна к равновесному сосуществованию с паровой фазой (рис.1 и 2).
Для паровой фазы имеется одна кривая конденсации Т (N 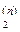 ) с двумя пересекающимися ветвями 1в и 2в, из которых 1в соответствует равновесию ж1–п, 2в – равновесию ж2–п (рис.1 и 2).
) с двумя пересекающимися ветвями 1в и 2в, из которых 1в соответствует равновесию ж1–п, 2в – равновесию ж2–п (рис.1 и 2).
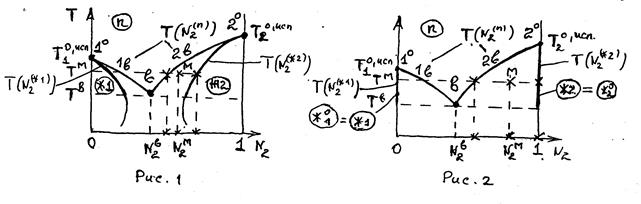
Граничные точки 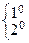 принадлежат одновременно
принадлежат одновременно 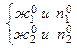 фазам, они характеризуют равновесия
фазам, они характеризуют равновесия 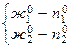 в чистых компонентах
в чистых компонентах 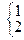 .
.
Внутренняя экстремальная точка в является пересечением двух ветвей 1в и 2в кривой конденсации Т (N 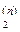 ), она принадлежит п. фазе, способной к равновесному сосуществованию одновременно с двумя ж. фазами ж1 и ж2 (так что А=3 и ω = 4–А = 4-3 =1).
), она принадлежит п. фазе, способной к равновесному сосуществованию одновременно с двумя ж. фазами ж1 и ж2 (так что А=3 и ω = 4–А = 4-3 =1).
При Т<Т 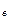 равновесия ж1–п и ж2–п не существуют, но возможно равновесие ж1– ж2.
равновесия ж1–п и ж2–п не существуют, но возможно равновесие ж1– ж2.
Точка М служит примером расчётной точки.
5.2.3. Законы смещения равновесий жидкость – пар в двухкомпонентных
системах (законы Гиббса – Коновалова ) при р –const.
5.3. Равновесие твердь – жидкость.
