Дифференциальное уравнение с разделяющимися переменными и его решение

Так называется дифференциальное уравнение вида

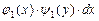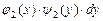+ = 0.

Делением обеих частей этого уравнения на 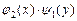, получаем дифференциальное уравнение с разделенными переменными

.

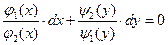Почленное интегрирование этого уравнения приводит к равенству

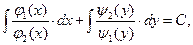
которое в неявной форме определяет решение исходного уравнения.

Линейное неоднородное дифференциальное уравнение первого порядка и его решение

Так называется уравнение вида

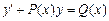, (3)

где Р(х), Q (x) — некоторые функции переменной х.

Решение этого уравнения можно найти методом Бернулли, который заключается в применении подстановки y = u · v, где u = u(x),
v = v(x) — некоторые неизвестные функции.

Линейное однородное дифференциальное уравнение второго порядка

Так называется уравнение вида

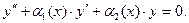(4)

Функции y₁(x), y₂(x) называются линейно независимыми, если равенство

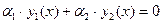(5)

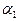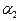( , — постоянные) возможно лишь в случае .

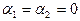Если хотя бы одна 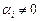(i = 1, 2), а тождество (5) возможно, то функции y₁(x), y₂(x), называются линейно зависимыми.

Пример. 1. y₁ = 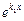, y₂ = 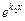—линейно независимые функции при .

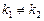2. y₁ = 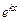, y₂ = 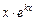— линейно независимые функции.

Теорема. Если y₁, y₂ — какие-либо два линейно независимые частные решения однородного линейного уравнения (4), то его общим решением служит функция y = C₁ y₁ + C₂ y₂ , где C₁, C₂ — произвольные постоянные.

Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Это будет уравнение вида

y'' + py' + qy = 0, где 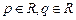. (6)

Для решения этого уравнения составляем и решаем соответствующее ему характеристическое уравнение

k² + pk + q = 0. (7)

При его решении в зависимости от дискриминанта D могут встретиться следующие три случая:

1. 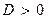. Тогда уравнение (7) имеет два различных действительных корня k₁ и k₂. Дифференциальное уравнение (6) имеет линейно независимые частные решения y₁ = 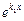, y₂ = .

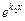При этом y = C₁ · 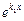+ C₂ · 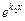— общее решение уравнения (6).

Пример. Для решения уравнения 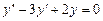составляем характеристическое уравнение 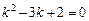. Отсюда k₁ = 2, k₂ = 1, y = 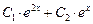— общее решение.

2. D = 0. Уравнение (7) имеет два равных действительных корня k₁ = k₂ = k. Уравнение (6) имеет линейно независимые частные решения y₁ = e^kx, y₂ = xe^kx. Тогда y = C₁ · 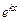+ C₂ · 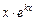— общее решение уравнения.

Пример. Уравнение 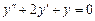имеет характеристическое уравнение k² + 2k + 1 = 0, откуда k₁ = k₂ = –1.

Тогда y = 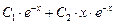— общее решение.

3. D < 0. Уравнение (7) не имеет решений во множестве R действительных чисел, но имеет решение во множестве C комплексных чисел (т. е. чисел вида 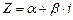, , 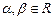i — мнимая единица, обладающая свойством i² = –1). Тогда уравнение (6) имеет линейно независимые частные решения , .

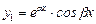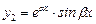При этом 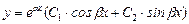— общее решение.

Пример. Уравнение 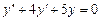имеет в качестве характеристического уравнение 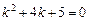. Решая его, имеем:

.

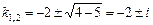Общим решением дифференциального уравнения будет

.
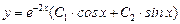