Подбор сечений балок равного сопротивления
Все предыдущие расчеты относились к балкам постоянного сечения. На практике мы имеем часто дело с балками, поперечные размеры которых меняются по длине либо постепенно, либо резко.
Ниже рассмотрено несколько примеров подбора сечения и определения деформаций балок переменного профиля.
Так как изгибающие моменты обычно меняются по длине балки то, подбирая ее сечение по наибольшему изгибающему моменту, мы получаем излишний запас материала во всех сечениях балки, кроме того, которому соответствует 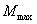 . Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления. Под этим названием подразумевают балки, у которых во всех сечениях наибольшее нормальное напряжение одинаково и должно быть равно допускаемому.
. Для экономии материала, а также для увеличения в нужных случаях гибкости балок применяют балки равного сопротивления. Под этим названием подразумевают балки, у которых во всех сечениях наибольшее нормальное напряжение одинаково и должно быть равно допускаемому.
Условие, определяющее форму такой балки, имеет вид
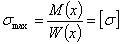
и
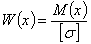
Здесь М(х) и W(x) — изгибающий момент и момент сопротивления в любом сечении балки; W(х) для каждого сечения балки должен меняться пропорционально изгибающему моменту.
Эти условия справедливы и для сечения с наибольшим изгибающим моментом; если обозначить  — момент сопротивления балки в сечении с наибольшим изгибающим моментом
— момент сопротивления балки в сечении с наибольшим изгибающим моментом 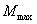 , то можно написать:
, то можно написать:
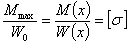 | (1) |
Покажем ход вычислений на примере. Рассмотрим балку пролетом l, защемленную концом А и нагруженную на другом конце силой Р (Рис.1). Выберем сечение этой балки в виде прямоугольника; задачу о надлежащем изменении момента сопротивления можно решать, меняя высоту или ширину балки или тот и другой размер вместе.
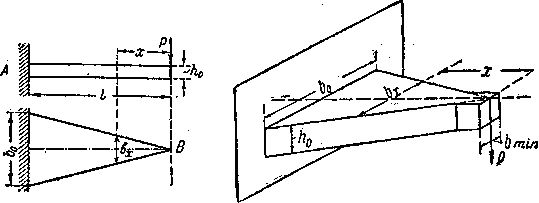
Рис.1. Расчетная схема балки равного сопротивления
Пусть высота балки будет постоянной 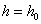 , а ширина переменной—
, а ширина переменной— 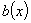 . Момент сопротивления в сечении на расстоянии х от свободного конца будет
. Момент сопротивления в сечении на расстоянии х от свободного конца будет 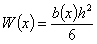 , а изгибающий момент
, а изгибающий момент 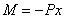 ; момент сопротивления опорного сечения
; момент сопротивления опорного сечения 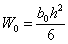 , a наибольший изгибающий момент в опорном сечении
, a наибольший изгибающий момент в опорном сечении 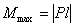 . В расчете имеют значения лишь абсолютные величины М(х) и
. В расчете имеют значения лишь абсолютные величины М(х) и 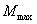
По формуле (1) получаем:
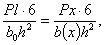
откуда
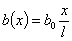
т. е. ширина меняется по линейному закону в зависимости от х. При 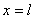 ширина равна
ширина равна 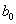 .
.
Вид балки в фасаде и плане показан на Рис.1. Такое очертание балки получается, если учитывать ее прочность только по отношению к нормальным напряжениям; ширина 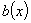 в сечении В обращается в нуль.
в сечении В обращается в нуль.
Однако необходимо обеспечить прочность и по отношению к касательным напряжениям. Наименьшая ширина балки, требуемая этим условием, определится из уравнения
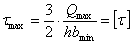
или, так как 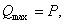
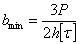
Таким образом, исправленное очертание балки предопределяет минимальный размер ширины и утолщение свободного края консоли.
