Дифференциальные уравнения первого порядка

1) Уравнения с разделяющимися переменными

Уравнение вида y¢ = f(x; y) называется уравнением с разделяющимися переменными, если его можно записать в виде

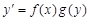(2)

или

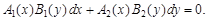(3)

Алгоритм решения:

1) в уравнении 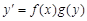производную у¢ представляем в виде отношения дифференциалов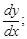

2) обе части уравнения умножаем на dx;

3) разделяем переменные: с помощью арифметических операций надо получить при dy функцию, зависящую только от переменной y, при dx – функцию, зависящую только от переменной x; в результате получается уравнение вида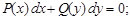

4) интегрируя, находим общий интеграл уравнения

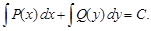
Пример 5.Найти общий интеграл дифференциального уравнения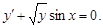

Решение

Представим уравнение в виде (2): 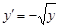sin x:

1) учитывая, что 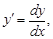получаем: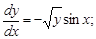

2) обе части уравнения умножаем на dx: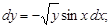

3) разделяем переменные, для этого обе части уравнения делим

на выражение 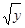, получаем: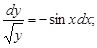

4) переносим все в одну часть равенства и интегрируем: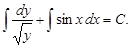

Таким образом, общий интеграл данного уравнения будет иметь вид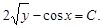

Тест 8. Дифференциальным уравнением c разделяющимися переменными является уравнение вида:

1)

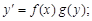
2)

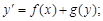
3) 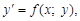где функция f(x; y) – однородная степени ноль;

4)

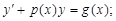
5)

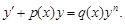
Тест 9.Дифференциальным уравнением c разделяющимися переменными является уравнение вида:

1)

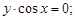
2)

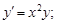
3)

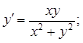
4)

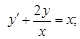
5)

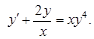
2) Однородные дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка y¢ = f(x; y) является однородным, если функция f(x; y) – однородная степени ноль по переменным x и у, т. е. обладает свойством: f(tx; ty) = f(x; y), для произвольного числа t ¹ 0.

Пример 6. Проверить, является ли однородной функция

f(x; y)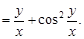

Решение

Функция является однородной функцией степени ноль, так как f(tx; ty) 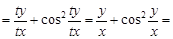f(x; y).

Однородное уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки y = u × x. Этой подстановкой мы вводим новую функцию u(x), оставляя независимую переменную прежней.

Пример 7. Проинтегрировать уравнение .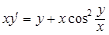

Решение

Приведем уравнение к виду y¢ = f(x; y), разделив обе части уравнения на x

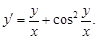(4)

Правая часть уравнения (4) является однородной функцией нулевой степени (см. пример 6), поэтому данное уравнение является однородным. Для его решения применим подстановку y = ux, тогда 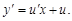Подставив два последних выражения в уравнение (4), получим

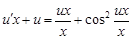
или

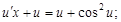
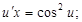
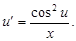
Полученное уравнение является уравнением с разделяющимися переменными.

Решаем его, используя ранее рассмотренный алгоритм

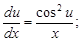
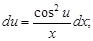
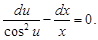
Интегрируем

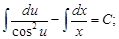
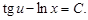
Подставив 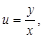найдем общий интеграл: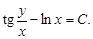

Тест 10.Однородным дифференциальным уравнением первого порядка является:

1)

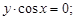
2)

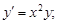
3)

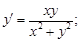
4)

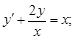
5)

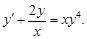
Тест 11. Однородным дифференциальным уравнением первого порядка является уравнение вида:

1) 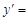f(x) g (y);

2) y¢ = f(x; y), где функция f(x; y) – однородная степени ноль;

3)

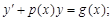
4)

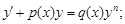
5) y = f(x; y), где функция f(x; y) – однородная.

Тест 12. Решение однородного дифференциального уравнения первого порядка может быть найдено в виде:

1) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции;

2) y = u × x, где 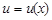– некоторая неизвестная функция;

3) y = u + v, где u = u(x) и v = v(x) – некоторые неизвестные функции;

4) y = u + x, где u = u(x) – некоторая неизвестная функция.

3) Линейные дифференциальные уравнения первого порядка

Уравнение вида

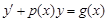(5)

называется линейным дифференциальным уравнением первого порядка.

Если g(x) = 0, то уравнение

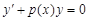(6)

называется линейным однородным.

Уравнение (6) является уравнением с разделяющимися переменными. Если в линейном уравнении g(x) ¹ 0, то оно называется линейным неоднородным.

Решение уравнения (5) может быть найдено в виде y = u × v,где
v = v(x) – некоторое решение уравнения 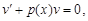u = u(x) – решение уравнения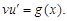

Пример 8.Решить дифференциальное уравнение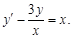

Решение

Решение этого линейного неоднородного уравнения будем искать в виде y = uv, где и и v – функции от х.

Подставив y и 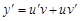в исходное уравнение, получим

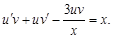
Группируя и вынося общий множитель за скобки, получим

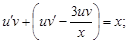
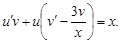(7)

Подбираем функцию v = v(x) так, чтобы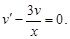

Имеем: 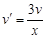– уравнение с разделяющимися переменными. Решаем его по ранее разобранному алгоритму и находим частное решение

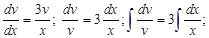
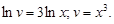
Полученное значение v подставим в уравнение (7) и будем иметь

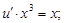
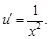
Откуда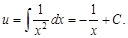

Общее решение исходного уравнения следующее:

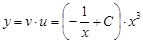или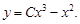

Тест 13. Линейным неоднородным дифференциальным уравнением первого порядка является уравнение вида:

1) 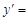f(x) g (y);

2) y¢ + p(x) y = q(x) yⁿ;

3) y¢ = f(x; y), где функция f(x; y) – однородная;

4)

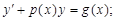
5)

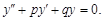
Тест 14. Линейным неоднородным дифференциальным уравнением первого порядка является уравнение вида:

1)

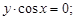
2)

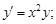
3)

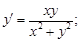
4)

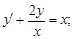
5)

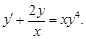
Тест 15.Решение линейного дифференциального уравнения первого порядка 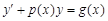может быть найдено в виде:

1) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции;

2) y = u × x, где u = u(x) – некоторая неизвестная функция;

3) y = u + v, где u = u(x) и v = v(x) – некоторые неизвестные функции;

4) y = u + x, где u = u(x) – некоторая неизвестная функция.

4) Уравнение Бернулли

Уравнением Бернулли называют нелинейное дифференциальное уравнение первого порядка вида

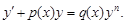
Решение уравнения Бернулли может быть найдено в виде y = uv, где u = u(x) и v = v(x).

Тест 16. Уравнением Бернулли является уравнение вида:

1) 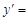f(x) g (y);

2) y¢ + p(x) y = q(x) yⁿ;

3) y¢ = f(x; y), где функция f(x; y) – однородная;

4)

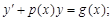
5)

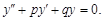
Тест 17. Уравнением Бернуллиявляется уравнение:

1)

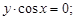
2)

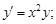
3)

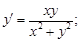
4)

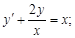
5)

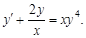
Тест 18. Решение уравнения Бернулли 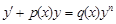может быть найдено в виде:

1) y = u × v, где u = u(x) и v = v(x) – некоторые неизвестные функции;

2) y = u × x, где u = u(x) – некоторая неизвестная функция;

3) y = u + v, где u = u(x) и v = v(x) – некоторые неизвестные функции;

4) y = u + x, где u = u(x) – некоторая неизвестная функция.

Ответы на тестовые задания

Номер теста

Правильный ответ

Номер теста
Правильный ответ