Тема 5. Дифференциальные уравнения

§1. Понятие о дифференциальном уравнении. Примеры торгово-экономических задач, приводящие к дифференциальным уравнениям. Порядок дифференциального уравнения. Семейство решений. Теорема существования и единственности решения (без доказательства). Задача Коши. Геометрическое истолкование решения. Общее и частное решение дифференциальногоуравнения.

Уравнения с разделяющимися переменными. Линейное уравнение первого порядка. Возможные случаи понижения порядка дифференциального уравнения (на примере уравнений второго порядка), когда в его записи отсутствуют независимая переменная или искомая функция.

Литература: [1, гл. 13, § 5], [2, гл. XXI, §1-5, 9], [3, гл. XVI, §79], [4, § 2. 14-2:17, стр. 99-108], [5, гл. XII, § 1 -3,7, 10], [7, гл. 14, § 1.1-1.3].

Упражнения: [5, упр. 2051, 2057, 2058, 2061, 2 Н 5, 2116], [6, упр. 5. 14-5.18, 5.21], [7, гл. 6, упр. 1-4, 10-13, 20-23, 43-46].

§ 2. Линейные дифференциальные уравнения второго порядка. Структура общего решения. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Характеристическое уравнение. Неоднородные линейные дифференциальные -уравнения второго порядка с постоянными коэффициентами. Подбор частных решений при специальном виде правой части.

Литература: [ 1, гл. 14], [2, гл. XXII, § 7, 11 - 13], [3, гл. XVI, §80], [4, § 2.18-2.21, cтp. 108-118], [5, гл. XII, § 8, 9], [7, гл. § 2].

Упражнения: [5, упр. 2184-2187, 2213 -2216, 2218], [6, упр. 5.22, 5.23, 5.25, 5.27, 5.29, 533, 5.37-5.39], [7,гл. 6, упр. 78-79, 84-87, 98-101, 104-106].

Тема 6. Ряды

§ 1. Числовые ряды. Сходимость ряда. Сумма ряда Свойства рядов. Необходимое условие сходимости ряда. Теорема сравнения. Признаки сходимости Даламбера, Коша.Знакочередующиеся ряды. Абсолютная и условная сходимость. Признак Лейбница.

Литература:[1, гл. 15], [2, гл. XXI, § 1 - 7], [3, гл. XI], [4, § 2.22-2.26, стр. 118-130], [5, гл. XIV, § 1], [7, гл. 8, § 1-3].

Упражнения:[5, упр. 2422-2424,2432, 2433, 2435, 2437], [6, упр. 6.1,6.15-6.18, 6.24,6.39-6.42], [7, гл. 8, упр. 31-34, 43-48].

§ 2. Степенные ряды. Радиус, интервал и область сходимости. Разложение элементарных функций в ряд Маклорена или Тейлора.

Литература: [1, гл. 16, § 1 -5], [2, гл. XXI, § 8 - 12, 14], [3, гл. XIJ, 65 - 68], [4, § 2.27 - 2.29, стр. 130-137], [5, гл. XIV, §3-4], [7, гл. 8. §4].

Упражнения: [5, упр. 2483 - 2486, 2492. 2), 3)], [6, упр. 6.77-6.80, 6.97, 6.1 Н, 6.1 15, 6.98], [7, гл. 8, упр. 103-106, 1 19-122].

§ 3. Использование рядов для приближенных вычислений.

Литература: [ 1, гл. 16, § 6], [2, гл. XXI, § 13], [3, гл. XII, § 69], [4, § 2.29, стр. 137-139], [5, гл. ХГУ, § 5].

Упражнения: [5, упр. 2512, 2518, 2520], [ 6 упр. 6.125-6.127].

ВОПРОСЫ ДЛЯ СДАЧИ ЭКЗАМЕНА (ЗАЧЕТА)

ТЕМА 1.

1.Сформулируйте определение понятия функции. Что называется областью определения функции? Какие функции называются элементарными? Какой вид имеют графики функций , ?.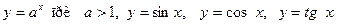

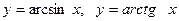Укажите области определения и множества значений этих функций. Какие из этих функций являются чётными?

2.При каких условиях число 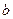называется пределом функции 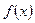при стремлении x к числу 2, к -∞, + ∞? Прочитайте формулы 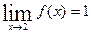, 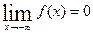и объясните их смысл.

5. Пределом какой функции при x→0 является число е? Найдите в учебнике значение числа ее двумя знаками после запятой. Как называется иобозначается логарифм числа x по основанию е? Какому числу равен предел ?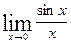

7.Какие правила применяются вычислении пределов суммы, разности и отношения двух функций?

8.Как определяется непрерывность функции 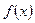в точке a?

ТЕМА 2.

1.Сформулируйте определение производной. Каков геометрический смысл производной?

2.Функция имеет производную в данной точке. Следует ли отсюда, что она непрерывна в этой точке?

3.Сформулируйте теоремы Ролла и Лагранжа. Каков геометрический смысл этих теорем? Сформулируйте теорему Коши.

4.В чем заключается правило Лопиталя? При каких условиях применяется правило Лопиталя? Перечислите различные типы неопределённостей, для раскрытия которых может быть использовано это правило. Приведите примеры.

5.Что называется дифференциалом функции? Приведите примеры.

6.Каковы признак» возрастания и убывания функции?

7.Что такое экстремум функции? Каковы необходимые и достаточные условия экстремума? Приведите примеры.

8.Приведите пример, показывающий, что обращение производнойв нуль не является достаточным условием экстремума.

9.Как найти интервалы выпуклости и точки перегиба графика функции? Приведите примеры.

ТЕМА 3.

1.Сформулируйте определение частных производных. •

2.Что называется полным приращением и полным дифференциалом функции двух переменных? Приведите примеры.

3.Каковы достаточные условия минимума (максимума) функции двух переменных. Что такое условный экстремум?

ТЕМА 4.

1.Сформулируйте определение первообразной функции. Докажите, что любые две первообразные одной и той же функции отличаются на константу.

2.Что называется неопределённым интегралом?

3.Какие правила применяются для вычисления неопределённого интеграла суммы функций, для вычисления ?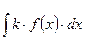

4.Выведите формулу интегрирования по частям.

5.Что называется интегральной суммой функции 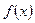нa отрезке [a',b].Какая фигура называется криволинейной трапецией? По какой формуле вычисляется её площадь?

6.Напишите формулу Ньютона-Лейбница.

7.Какие свойства определённого интеграла Вам известны?