Уравнение плоской бегущей волны
Задача: получить уравнение, позволяющее рассчитывать смещение любой точки упругой среды, в которой распространяется волновой процесс, в любой момент времени.
Решение:
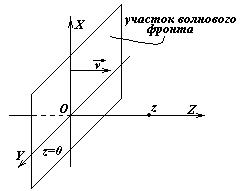 Пусть вдоль оси Oz распространяется плоская монохроматическая волна с частотой w: это значит, что вектор скорости волны v направлен вдоль OZ, а волновые фронты перпендикулярны этой оси.
Пусть вдоль оси Oz распространяется плоская монохроматическая волна с частотой w: это значит, что вектор скорости волны v направлен вдоль OZ, а волновые фронты перпендикулярны этой оси.
Пусть смещения точек в плоскости z = 0 происходят по закону
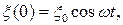
где x0 - амплитуда колебания точек в плоскости z =0; t - время колебания точек плоскости z = 0.
Тогда зависимость смещения точек, имеющих координату z, будет зависеть от времени следующим образом:
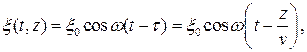
где t - время запаздывания , то есть то время, которое потребовалось волновому процессу, чтобы распространиться на расстояние z. Очевидно, что время колебания точек с координатой z меньше времени колебания точек с координатой z = 0 на время запаздывания 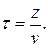
Уравнение 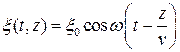 носит название уравнения плоской бегущей волны.
носит название уравнения плоской бегущей волны.
Обратите внимание – уравнение бегущей волны – это функция двух переменных – координаты z и времени t. Зафиксировав координату точки, вы получаете зависимость ее смещения от времени. Зафиксировав время, вы получаете картину мгновенного распределения смещений точек среды, в которой распространяется волна.
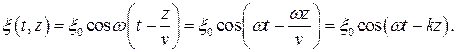 |
Чаще всего уравнение бегущей волны записывают иначе. Преобразуем наше уравнение
Отношение циклической частоты w к скорости волны v обозначили за k – волновое число:
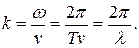
Физический смысл волнового числа: волновое число показывает, как изменяется фаза волны при перемещении на 1 м вдоль направления распространения волны.
В связи с этим произведение kz в уравнении бегущей волны называют запаздыванием по фазе или набегом фазы.
Аналогичное уравнение можно записать для случая волн другой формы. Необходимо лишь учесть изменение амплитуды колебания точек по мере удаления от источника колебаний. Например,
для цилиндрической волны
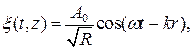 |
где r – расстояние от прямой, являющейся источником волны;
для сферической волны
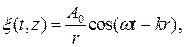 |
где r – расстояние до точки, являющейся источником колебаний.
Уравнение бегущей волны позволяет установить связь между скоростью, длиной волны и частотой. Смещения точек, находящихся на расстоянии в длину волны, одинаковые:
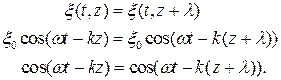
Значения косинусов для двух различных аргументов будут одинаковы, если аргументы отличаются на 2π. после
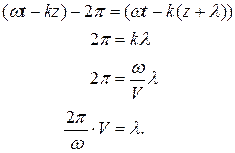
С учетом того, что 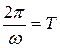 , получаем
, получаем 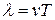 . Видим, что длина волны λ – это расстояние, которое проходит волна за время, равное периоду колебания одной частицы.
. Видим, что длина волны λ – это расстояние, которое проходит волна за время, равное периоду колебания одной частицы.
Фазовая и групповая скорости волн
Уточним введенное ранее понятие скорости волны. Допустим, в пространстве распространяется монохроматичная волна (волна одной частоты). Уравнение плоской волны имеет 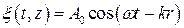 . Аргумент косинуса
. Аргумент косинуса 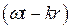 - это фаза. Зафиксируем значение фазы – тем самым мы зафиксируем определенное смещение точки от положения равновесия, допустим «горб» волны. С течением времени слагаемое
- это фаза. Зафиксируем значение фазы – тем самым мы зафиксируем определенное смещение точки от положения равновесия, допустим «горб» волны. С течением времени слагаемое 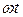 изменяется, значит, слагаемое
изменяется, значит, слагаемое 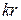 тоже должно изменяться, чтобы разность оставалась неизменной. Это означает, что зафиксированный нами «горб» волны перемещается в пространстве. Скорость перемещения этого «горба» (фазы) называется фазовой скоростью волны. Для нахождения фазовой скорости продифференцируем выражение
тоже должно изменяться, чтобы разность оставалась неизменной. Это означает, что зафиксированный нами «горб» волны перемещается в пространстве. Скорость перемещения этого «горба» (фазы) называется фазовой скоростью волны. Для нахождения фазовой скорости продифференцируем выражение 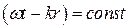 по времени:
по времени:
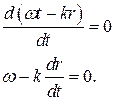
Производная от расстояния по времени 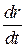 - это не что иное, как скорость перемещения фазы в пространстве, т.е. фазовая скорость
- это не что иное, как скорость перемещения фазы в пространстве, т.е. фазовая скорость 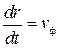 . С учетом того, что
. С учетом того, что 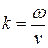 , получаем
, получаем
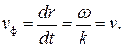
Таким образом, скорость, входящая в уравнение бегущей волны, – это фазовая скорость.
В общем случае фазовая скорость зависит от частоты волны, т.е. волны разных частот в одной и той же среде распространяются с разной скоростью. Это явление называется дисперсией.
Допустим, в пространстве распространяется группа волн – «волновой пакет». Мы наблюдаем результат наложения этих волн. Например, волновой пакет состоит всего из двух волн близких частот ω1 и ω2. На рисунке показаны распределение смещений частиц среды ξ1 и ξ2 вдоль оси ОХ в какой-то момент времени. Ниже показана картина наложения смещений частиц. Видно, что будут области, где смещение частиц от положения равновесия максимально. Эти области называют «горбами» волны.
Если волны, образующие волновой пакет, не обладают дисперсией, то картинка наложения волн, перемещаясь в пространстве, не изменяет своей формы.
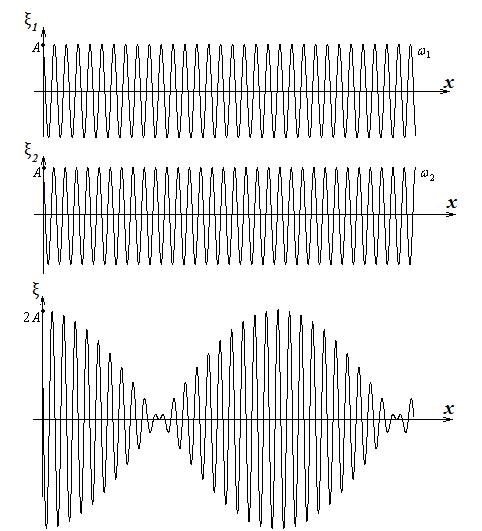
Если составляющие волнового пакета перемещаются с разными скоростями, то картинка наложения волн с течением времени видоизменяется. «Горб» картины наложения будет перемещаться в пространстве, но его скорость будет отличиться от скорости распространения отдельных составляющих волнового пакета. Скорость перемещения максимума волнового пакета называют групповой скоростью. Найдем связь групповой скорости с фазовой.
Пусть первая волна длиной λ распространяется со скоростью 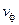 . Вторая волна длиной (λ+dλ) распространяется со скоростью
. Вторая волна длиной (λ+dλ) распространяется со скоростью 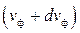 . В какой-то момент времени «горб» волнового пакета совпадает с точкой А.
. В какой-то момент времени «горб» волнового пакета совпадает с точкой А.
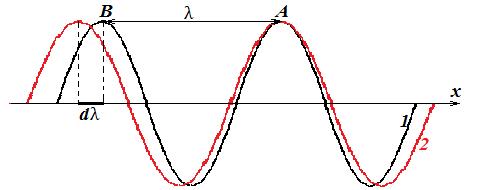
Вторая волна догоняет первую со скоростью 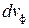 , и в системе отсчета, связанной с первой волной, через время
, и в системе отсчета, связанной с первой волной, через время 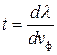 «горб» волнового пакета совпадет с точкой В. Очевидно, что в лабораторной системе отсчета скорость перемещения «горба» будет меньше скорости первой волны
«горб» волнового пакета совпадет с точкой В. Очевидно, что в лабораторной системе отсчета скорость перемещения «горба» будет меньше скорости первой волны
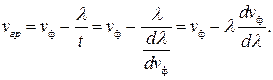
В рассмотренном примере вторая, более длинная волна, распространялась быстрее первой, более короткой волны ( 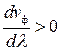 ). Этот случай называют нормальной дисперсией. Групповая скорость в этом случае оказывается меньше фазовой.
). Этот случай называют нормальной дисперсией. Групповая скорость в этом случае оказывается меньше фазовой.
Если более короткие волны в пакете будут бежать быстрее длинных ( 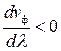 ), то групповая скорость окажется больше фазовой. Это так называемая аномальная дисперсия.
), то групповая скорость окажется больше фазовой. Это так называемая аномальная дисперсия.
В жизни практически всегда приходится сталкиваться не с бесконечной монохроматичной волной, а с волновым пакетом. Поэтому скорость волны, измеряемая на практике, это чаще всего групповая скорость.
В дальнейшем мы будем рассматривать в основном идеальный случай – бесконечную синусоидальную волну. Поэтому всюду, если это не оговорено особо, под скоростью волны будем понимать фазовую скорость.
Волновое уравнение
Для доказательства существования в системе свободных гармониче-
ских колебаний, необходимо было получить дифференциальное уравнение вида 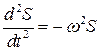 . Из дифференциального уравнения можно было определить циклическую частоту собственных колебаний ω и, следовательно, рассчитать период колебаний
. Из дифференциального уравнения можно было определить циклическую частоту собственных колебаний ω и, следовательно, рассчитать период колебаний 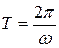 .
.
Можно предположить, что наличие в системе волнового процесса тоже описывается дифференциальным уравнением. Каков вид этого уравнения? Какие характеристики волнового процесса можно определить из этого уравнения?
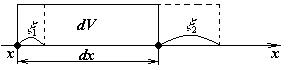
Рассмотрим длинный твердый стержень, вдоль которого бежит продольная волна. Распространение продольной волны связано с возникновением в теле деформации растяжения-сжатия. Кроме того, все точки среды, по которой бежит волна, двигаются.
Пусть малый участок стержня длиной 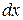 , расположенный между сечениями стержня с координатами x и
, расположенный между сечениями стержня с координатами x и 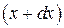 , испытывает деформацию растяжения.
, испытывает деформацию растяжения.
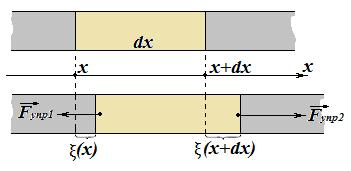
где 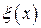 - смещение от положения равновесия точек, находящихся в левом сечении рассматриваемого участка стержня и имеющих координату х;
- смещение от положения равновесия точек, находящихся в левом сечении рассматриваемого участка стержня и имеющих координату х;
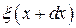 - смещение от положения равновесия точек, находящихся в правом сечении рассматриваемого участка стержня и имеющих координату
- смещение от положения равновесия точек, находящихся в правом сечении рассматриваемого участка стержня и имеющих координату 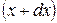 .
.
На выделенный участок стержня действуют силы упругости 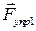 и
и 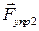 со стороны растянутых соседних участков стержня. Строго говоря, скорости и ускорения различных точек рассматриваемого участка разные, но ввиду малости участка
со стороны растянутых соседних участков стержня. Строго говоря, скорости и ускорения различных точек рассматриваемого участка разные, но ввиду малости участка 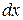 отличием скоростей и ускорений можно пренебречь. Запишем для выделенного участка стержня
отличием скоростей и ускорений можно пренебречь. Запишем для выделенного участка стержня 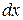 второй закон Ньютона:
второй закон Ньютона:
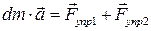 ,
,
где 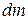 - масса рассматриваемого участка.
- масса рассматриваемого участка.
В проекции на ОХ:
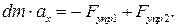
Масса рассматриваемого участка стержня 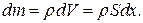
По определению проекция ускорения 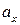 – это вторая производная от смещения по времени
– это вторая производная от смещения по времени 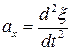 .
.
Силы упругости могут быть рассчитаны через напряжения в соответствующих сечениях: 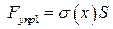 и
и 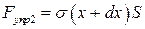 .
.
После подстановки получаем
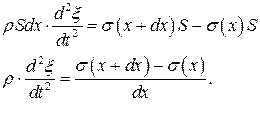
Очевидно, что отношение 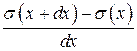 - это не что иное, как производная от напряжения по координате
- это не что иное, как производная от напряжения по координате 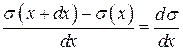 .
.
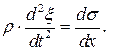 (*)
(*)
Согласно закону Гука напряжение прямо пропорционально относительному удлинению 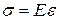 , где Е – модуль упругости вещества или модуль Юнга. Относительное удлинение ε – это отношение абсолютного удлинения к начальной длине образца. В нашем случае абсолютное удлинение равно
, где Е – модуль упругости вещества или модуль Юнга. Относительное удлинение ε – это отношение абсолютного удлинения к начальной длине образца. В нашем случае абсолютное удлинение равно 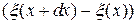 , а первоначальная длина рассматриваемого участка -
, а первоначальная длина рассматриваемого участка - 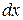 . Тогда относительное удлинение
. Тогда относительное удлинение 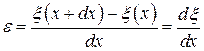 - производная от смещения по координате. Подставляем значение относительного удлинения в уравнение (*):
- производная от смещения по координате. Подставляем значение относительного удлинения в уравнение (*):
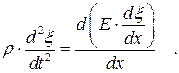
С учетом того, что модуль Юнга Е – это постоянная величина, получаем уравнение
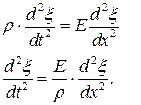
Нетрудно показать, что если ввести обозначение 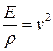 , то решением уравнения
, то решением уравнения 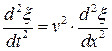 является уравнение плоской бегущей волны
является уравнение плоской бегущей волны 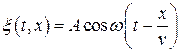 .
.
Подведем итоги
1 Если для какой-либо системы удается получить дифференциальное уравнение вида 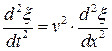 , то в системе распространяется волновой процесс. По этой причине дифференциальное уравнение
, то в системе распространяется волновой процесс. По этой причине дифференциальное уравнение 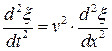 называется волновым уравнением.
называется волновым уравнением.
2 Волновое уравнение позволяет определить скорость волны v. Константа, стоящая в волновом уравнении перед второй производной по координате, - это величина, равная квадрату скорости волны.
В нашем случае получено значение скорости продольной волны в твердом теле 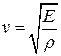 (как уже было сказано выше).
(как уже было сказано выше).
Энергия упругой волны
Процесс распространения упругой волны связан с вовлечением в колебательное движение частиц среды. Любое же колеблющееся тело обладает энергией, следовательно, можно говорить о передаче энергии колебательного движения от одних частиц среды другим. Иными словами, упругая волна переносит энергию.
Пусть в некоторой области пространства вдоль оси ОХ распространяется плоская продольная волна. Ее уравнение имеет вид
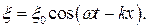
Рассмотрим малый элемент объема dV среды, в которой распространяется волна. Частицы среды, находящиеся в выделенном нами объеме, двигаются, участвуя в колебательном движении, а значит, они обладают кинетической энергией. Поскольку выбранный нами элемент объема очень мал, можно считать, что все его точки имеют одинаковые скорости. Тогда кинетическая энергия выделенного объема может быть рассчитана как
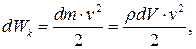
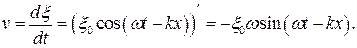 |
где r - плотность упругой среды, v – скорость всех точек выделенного нами объема. Скорость колебательного движения может быть найдена как производная от смещения по времени:
Тогда кинетическая энергия выделенного объема будет равна:
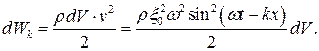 |
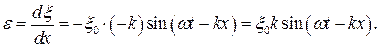 |
 Распространение волны связано с деформацией упругой среды. Величина относительной деформации выделенного нами участка равна
Распространение волны связано с деформацией упругой среды. Величина относительной деформации выделенного нами участка равна 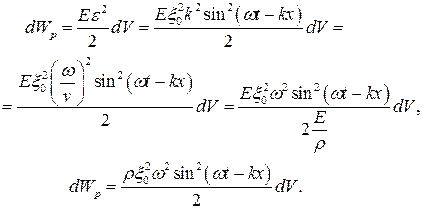 |
Потенциальная энергия упругой деформации выделенного объема dV:
Интересно!! Кинетическая и потенциальная энергии выделенного объема упругой среды (он, кстати, был выбран произвольно) одинаковы, более того, они меняются в одной фазе (в отличие от кинетической и потенциальной энергий колеблющегося маятника).
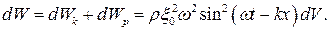 |
Полная энергия выделенного участка
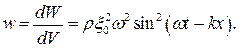 |
Плотность энергии волны (энергия единицы объема)
Видно, что плотность энергии любого участка среды, в которой распространяется волна, меняется с течением времени – переносится, передается от одних частиц другим.
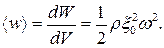 |
Среднее за период значение квадрата синуса равно ½, следовательно, средняя за период плотность энергии волны будет равна
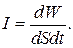 |
Обычно, для характеристики волновых процессов пользуются понятием интенсивности волны. Интенсивностью волны называют энергию, переносимую волной за 1 секунду через поверхность площадью в 1 м2, расположенную перпендикулярно скорости распространения волны.
Рассчитаем интенсивность волны.
Через площадку dS за время dt будет перенесена энергия, заключенная в объеме цилиндра с основанием dS и высотой vdt. Поскольку размеры цилиндра очень малы, можно считать плотность энергии в каждой его точке одинаковой. Тогда: 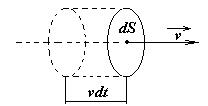
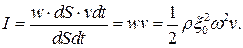 |
Интенсивность волны прямо пропорциональна:
1 плотности среды;
2 квадрату амплитуды волны(эта зависимость характерна для волнового процесса любой природы) ;
3 квадрату частоты волны;
4 скорости волны.
Если волна плоская, то ежесекундно в колебательное движение вовлекается одинаковое количество частиц, волновой фронт проходит через поверхность одинаковой площади. Это значит интенсивность волны везде одинаковая, следовательно, амплитуды колебания всех точек среды одинаковые.
Если волна сферическая, то волновыми поверхностями для нее будут сферы. Энергия, переносимая волной за секунду через каждую сферу одинакова, а вот интенсивность волны будет убывать обратно пропорционально площади поверхности, то есть обратно пропорционально расстоянию до источника волны:
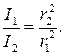 |
Тогда амплитуда колебания точек в сферической волне будет убывать обратно пропорционально расстоянию до источника волны:
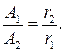
Выводы, полученные нами, справедливы и для поперечной волны.
Мы рассмотрели идеальный случай незатухающей волны. В реальной плоской волне амплитуда и интенсивность убывают с расстоянием по закону
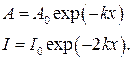
Энергия волны поглощается средой, в которой она распространяется.
§2 Примеры решения задач
Задача 1 Скорость и длина разных видов волн в твердом теле
Рассчитайте скорость и длину волны, частота которой f = 400 Гц, в стали в случаях:
а) вдоль стального стержня бежит продольная волна;
б) вдоль стержня бежит поперечная волна;
в) волна бежит по струне д линой сечением 1 мм2, натянутой силой
200 Н.
Решение:
Скорость волны зависит не только от среды, в которой она распространяется, но и от вида волны. В одной и той же среде скорость разных волн разная.
1 Скорость продольной волны равна 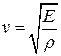 , где Е - модуль Юнга,
, где Е - модуль Юнга, 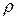 - плотность вещества.
- плотность вещества. 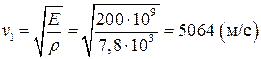 .
.
2 Скорость поперечной волны равна 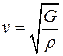 , где G - модуль сдвига,
, где G - модуль сдвига, 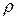 - плотность вещества.
- плотность вещества. 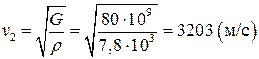 .
.
3 Скорость поперечной волны в натянутой струне 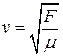 , где F – сила натяжения струны,
, где F – сила натяжения струны, 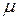 - погонная масса. Погонная масса или масса единицы длины равна
- погонная масса. Погонная масса или масса единицы длины равна 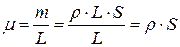 .
.
Тогда скорость 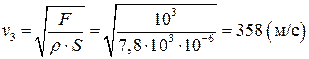 .
.
Нетрудно видеть, что быстрее всего в веществе распространяются продольные волны.
Длина волны связана со скоростью и частотой 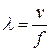 .
.
Длина продольной волны 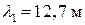 , поперечной волны
, поперечной волны 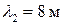 , волны в струне
, волны в струне 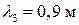 .
.
Задача 2 Интенсивность сейсмической волны
На расстоянии 100 км от очага землетрясения зафиксирована сейсмическая волна интенсивностью 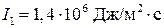 . Чему была рана интенсивность волны в точке, расположенной на расстоянии 2 км от очага землетрясения? Чему равна мощность, приходящаяся на поверхность площадью
. Чему была рана интенсивность волны в точке, расположенной на расстоянии 2 км от очага землетрясения? Чему равна мощность, приходящаяся на поверхность площадью
20 м2, на расстоянии 2 км от очага землетрясения?
Решение:
1 От очага землетрясения волна распространяется по всем направлениям, то есть волна сферическая. Интенсивность сферической волны обратно пропорциональна квадрату расстояния до источника волны 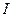 ~
~ 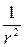 .
.
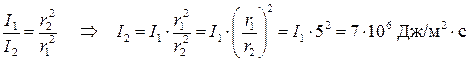 .
.
2 По определению интенсивность волны – это 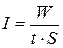 .
.
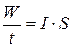 – мощность, приходящаяся на поверхность площадью S.
– мощность, приходящаяся на поверхность площадью S.
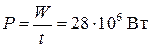 .
.
Задача 3 Частота звука, записанного на грампластинке
В канавке грампластинки, вращающейся со скоростью 33 об/мин, на расстоянии 12,5 см от оси вращения «бугорки» располагаются с интервалом 2,45 мм. Чему равна частота записанного в этом месте звука?
Решение:
1 Частота звука совпадает с частотой колебания иголки. Игла совершает вынужденные колебания под действием толчков со стороны «бугорков». Частота же вынужденных колебаний совпадает с частотой внешней вынуждающей силы. Следовательно, частота звука равняется частоте следования толчков со стороны «бугорков» на иголку. Найдем число «бугорков», которые проходят под иголкой за 1 с.
Линейная скорость точек грампластинки, располагающихся на расстоянии R = 12 см от оси вращения:
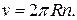
2 Найдем длину дуги окружности, проходящей под иголкой за время 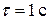 :
:
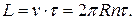
3 Найдем число «бугорков» на длине дуги L, если расстояние между соседними «бугорками» равно S = 2,45 мм:
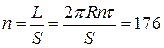
Частота звука 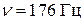 .
.
Задача 4 Графическое изображение волны
Конец длинной горизонтальной натянутой струны совершает гармоническое колебание с частотой 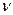 = 250 Гц. Сила натяжения струны F = 75 Н, а погонная плотность
= 250 Гц. Сила натяжения струны F = 75 Н, а погонная плотность 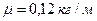 . В начальный момент времени конец струны движется из положения равновесия вверх со скоростью 4 м/с. Постройте
. В начальный момент времени конец струны движется из положения равновесия вверх со скоростью 4 м/с. Постройте
а) график зависимости смещения частиц струны от их расстояния до конца струны через 0,01 с;
б) график зависимости смещения точки струны, расположенной на расстоянии 0,1 м от ее конца.
Решение:
Составляем уравнение бегущей по струне волны. Ось координат ОХ
направим вдоль струны, начало координат совмести с колеблющимся концом. Волна бежит в положительном направлении оси ОХ.
1 Циклическая частота волны 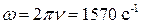 .
.
2 Амплитуда колебаний всех частиц струны такая же, как амплитуда колебаний ее конца. Конец струны пришел в колебательное движение из положения равновесия, следовательно, его скорость в начальный момент времени была максимальна. Амплитуда колебаний связана с начальной скоростью соотношением 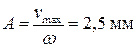 .
.
3 Скорость волны в натянутой струне 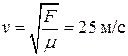 .
.
4 Волновое число 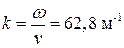 .
.
5 Уравнение колебаний свободного конца струны, являющегося источником волны 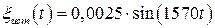 .
.
Уравнение бегущей вдоль струны волны
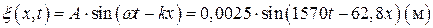 .
.
6 Уравнение бегущей волны 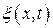 - есть функция двух переменных
- есть функция двух переменных 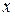 и
и 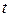 .
.
Зафиксировав время, можно получить 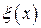 -картину распределения смещений частиц струны . По условию t = 0,01 с, тогда
-картину распределения смещений частиц струны . По условию t = 0,01 с, тогда 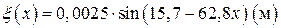 . Смещение частиц выглядит так:
. Смещение частиц выглядит так:
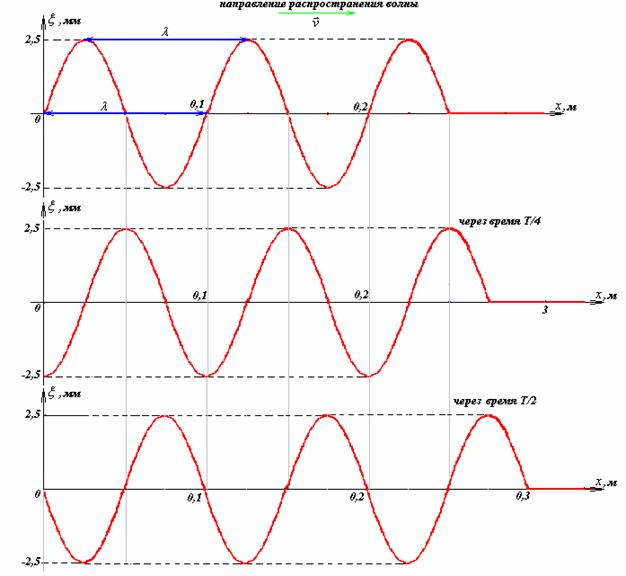
По существу, график 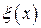 при t = const является профилем (фотографией) струны, по которой бежит волна.
при t = const является профилем (фотографией) струны, по которой бежит волна.
За время, равное 0,01с волна ушла от конца струны на расстояние
0,25 м. Видим, что минимальное расстояние между точками, колеблющимися одинаково, то есть длина волны, равна 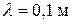 .
.
Зависимость смещения точки струны, расположенной на расстоянии 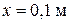 , выглядит так
, выглядит так 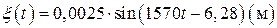 .
.
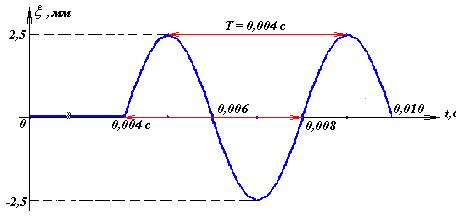
В течение времени 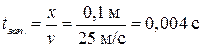 точка покоилась, затем пришла в колебательное движение с такой же частотой, как источник волны.
точка покоилась, затем пришла в колебательное движение с такой же частотой, как источник волны.
Задача 5 Определение разности фаз между точками в волне
Поперечная волна распространяется вдоль натянутого шнура со скоростью 25 м/с. Период колебаний точек шнура Т = 1 с, амплитуда А = 2 см. Определите разность фаз между точками шнура, находящимися на расстояниях 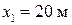 и
и 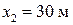 от источника волны.
от источника волны.
Ответ: 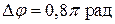
Решение:
1 Определяем циклическую частоту колебаний точек шнура 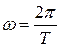 .
.
2 Определяем волновое число 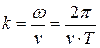 .
.
3 Записываем уравнение бегущей волны
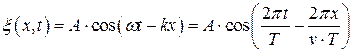 .
.
4 Фаза – это аргумент косинуса в уравнении волны.
Фаза первой точки 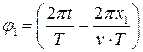 , фаза второй точки
, фаза второй точки 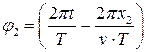 .
.
Разность фаз 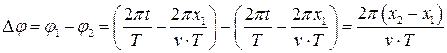
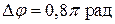
§3 Задания для самостоятельного решения
Тест «Механические волны»
1 Механическая или упругая волна – это процесс…
А) Колебания поверхности твердого тела или жидкости;
Б) Колебания вещества под действием внешней вынуждающей силы;
В) Возникновения свободных колебаний в упругой среде, возникающий при деформации;
Г) Распространения колебаний в упругой среде.
2 По характеру колебания частиц в волне относительно ее направления распространения волны делят на … (укажите все виды волн)
А) Поперечные; Б) Сферические; В) Плоские;
Г) Продольные; Д) Поверхностные; Е) Цилиндрические.
3 Укажите, какой вид деформации возникает в среде при распространении упругой волны, и в каких средах могут распространяться волны разных видов.
| Вид волны | Деформация, возникающая при распространении волны | Среда, в которой может распространяться волна |
| Продольная | ||
| Поперечная | ||
| Варианты ответов | А) Растяжения –сжатия; Б) Изгиб; В) Сдвиг; Г) Кручение; Д) Все виды деформации. | А) Газ; Б) Жидкость; В) Твердое тело; Г) Любая упругая среда. |
4 Фронтом волны называют…
А) Геометрическое место точек, которые уже участвуют в колебательном движении;
Б) Геометрическое место точек, которые еще не участвуют в колебательном движении;
В) Геометрическое место точек, до которых дошел волновой процесс.
5 Если какое-либо тело начинает колебаться, то от него побежит упругая волна. Причина возникновения этой волны - …
А) Взаимодействие молекул упругой среды, окружающей колеблющееся тело;
Б) Толчки, которые испытывает упругая среда под действием колеблющегося тела;
В) Деформация среды, окружающей колеблющееся тело;
Г) Способность молекул упругой среды, окружающей колеблющееся тело, двигаться;
6 В процессе распространения упругой волны переносятся…
А) Энергия; Б) Импульс; В) Вещество;
Г) Деформация; Д) Информация.
7 Частота колебания частиц среды при распространении в ней упругой волны зависит только от…
А) Упругих свойств среды, в которой распространяется волна;
Б) Частоты колебания источника волны;
В) Температуры среды, в которой распространяется волна;
Г) Наличия в среде механических напряжений.
8 Заполните таблицу «Физические величины, характеризующие упругую волну».
| Физическая величина, характеризующая волну | Физический смысл величины |
| Амплитуда волны, А | |
Частота волны , 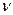 | |
| Скорость волны,v | |
Длина волны, 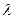 | |
| Интенсивность волны, I |
А) Это частота колебания частиц в волне;
Б) Это расстояние между точками, которые колеблются в одной фазе;
В) Это энергия колебания всех частиц в единице объема;
Г) Это скорость колебания частиц в волне;
Д) Это амплитуда колебания источника волны;
Е) Это средняя за период энергия, переносимая волной в единицу времени через поверхность единичной площади, расположенную перпендикулярно направлению распространения волны;
Ж) Это расстояние, на которое распространяется возмущение в упругой среде в единицу времени;
З) Это расстояние между гребнем и впадиной волны;
И) Это минимальное расстояние между точками, которые колеблются одинаково;
К) Это амплитуда колебания частиц в волне.
9 Как связаны амплитуда и интенсивность волны?
А) А ~ I; Б) A ~ I2; В) I ~ 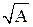 ; Г) I ~ A2.
; Г) I ~ A2.
10 Как зависят амплитуда и интенсивность плоской и сферической волн от расстояния до источника волны? Затуханием колебаний при распространении волны пренебречь.
А) A = const, I = const как для плоской, так и для сферической волны;
Б) А ~ 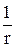 , I ~
, I ~ 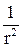 как для плоской, так и для сферической волны;
как для плоской, так и для сферической волны;
В) A = const, I = const для плоской волны,
А ~ 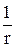 , I ~
, I ~ 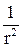 для сферической волны;
для сферической волны;
Г) A = const, I = const для сферической волны,
А ~ 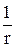 , I ~
, I ~ 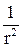 для плоской волны.
для плоской волны.
11 Сравните амплитуды и интенсивности сейсмической Р-волны на расстояниях 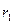 = 10 км и
= 10 км и 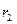 = 20 км от очага землетрясения.
= 20 км от очага землетрясения.
А) 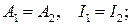 Б)
Б) 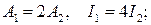
В) 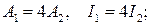 Г)
Г) 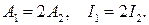
12 Уравнение бегущей поперечной волны имеет вид 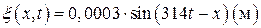 . Определите скорость распространения волны.
. Определите скорость распространения волны.
А) 1 м/с; Б) 6,26 м/с; В) 314 м/с; Г) 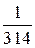 м/с.
м/с.
13 Плоская волна распространяется вдоль оси OY. По графикам зависимости смещения частиц от времени и координаты определите скорость волны.
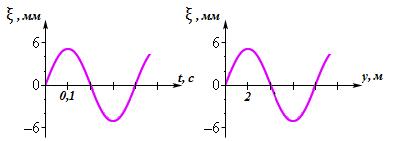
А) 0, 8 м/c; Б) 3,2 м/c; В) 20 м/c; Г) 40 м/c.
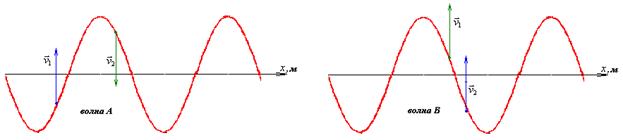 14 На рисунке изображен профиль волны и скорость двух ее точек. В каком направлении распространяется волна?
14 На рисунке изображен профиль волны и скорость двух ее точек. В каком направлении распространяется волна?
А) Обе волны распространяются вправо;
Б) Обе волны распространяются влево;
В) Волна А распространяется вправо, волна В – влево;
Г) Волна А распространяется влево, волна В - вправо.
15 Каково минимальное расстояние между точками волны, колеблющимися в противофазе? Длина волны λ = 8 см.
А) 2 см; Б) 4 см; В) 8 см.
Задачи
1 Поперечная волна, бегущая по веревке, описывается уравнением описывается уравнением 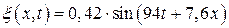 , где
, где 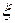 и
и 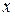 измеряются в метрах, t в секундах. Определите: направление распространения волны; амплитуду колебаний точек в волне; частоту волны; длину волны; скорость волны; максимальную скорость колебаний частиц веревки.
измеряются в метрах, t в секундах. Определите: направление распространения волны; амплитуду колебаний точек в волне; частоту волны; длину волны; скорость волны; максимальную скорость колебаний частиц веревки.
2 Вычислите скорость и длину продольной волны, частота которой
f = 400 Гц, в граните, воде и воздухе при 200 С.
Справочные данные: модуль Юнга гранита Е = 45 ГПа; коэффициент всестороннего сжатия воды В = 2,2 ГПа; плотность гранита 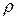 = 2600 кг/м3; молярная масса воздуха М = 29 г/моль.
= 2600 кг/м3; молярная масса воздуха М = 29 г/моль.
3 Два динамика испускают звуковые волны в противофазе. Частоты волн одинаковы и равны 170 Гц. Чему равна разность фаз волн, приходящих в точку, расположенную на расстояниях 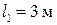 и
и 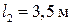 от динамиков? Скорость звука принять равной 340 м/с.
от динамиков? Скорость звука принять равной 340 м/с.
4 Сейсмические S- и Р-волны (продольные и поперечные) распространяются со скоростями 9 км/с и 5 км/с соответственно. Определите расстояние до очага землетрясения, если сейсмическая станция зафиксировала приход этих волн с интервалом τ = 2 мин.
5 По торцу длинного стального стержня нанесли удар молотком. Определите длину L стержня, если короткий упругий импульс, отразившись от второго торца, возвратился к месту удара через время τ = 10–3 с. Модуль Юнга стали E = 1,9·1011 Н/м2 , плотность стали ρ = 7,6∙103 кг/м3 .
6 При помощи эхолота измерялась глубина моря. Промежуток времени между испусканием звукового импульса и его приемом после отражения от дна оказался равным τ = 2,50 с. Плотность морской воды ρ = 1030 кг/м3, коэффициент сжимаемости воды k = 4,6·10–10 Па–1. Определите глубину H моря.
§4 Звук
Звуком называют механическую волну с частотой от 20 до 20000 Гц. Значимость этого вида упругих волн определяется тем, что звук воспринимается нашим ухом и используется как источник информации.
Волны с частотами ниже 20 Гц называют инфразвуком, выше 20000 Гц – ультразвуком.
Скорость звука в жидкостях и газах
