Получение случайных чисел в табличном процессоре Excel

Для создания имитационных моделей широко применяется метод статистического моделирования (метод Монте-Карло), позволяющий получать на компьютере выборки псевдослучайных чисел с заданными законами распределения.

При построении имитационных моделей экономических объектов широко используется базовый равномерный закон распределения, с помощью которого затем можно получить любое другое распределение.

Непрерывное равномерное распределение моделирует встроенная функция MS Excel

=СЛЧИС( ) (1)

из категории «Математические», которая возвращает случайное число из интервала [0; 1].

Если требуется получить равномерное дискретное распределение целых чисел в интервале [X, Y], то в MS Excel можно воспользоваться формулой:

=ЦЕЛОЕ(Х+(Y-X+1)*СЛЧИС()). (2)

Здесь X, Y – левая и правая границы диапазона псевдослучайных дискретных чисел. Встроенная функция ЦЕЛОЕ() возвращает целую часть от результата вычисления Х+(Y-X+1)*СЛЧИС().

Например, для получения выборки псевдослучайных целых чисел из интервала [5; 18], необходимо в Excel ввести формулу:

=ЦЕЛОЕ(5+(18-5+1)*СЛЧИС()).

При создании имитационных моделей экономических систем бывает необходимо получить выборки псевдослучайных чисел с различными законами распределения. Из теории вероятности известно фундаментальное соотношение

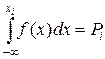, (3)

где 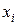– случайные числа с заданным законом распределения; 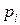– случайные числа с равномерным законом распределения в диапазоне от 0 до 1, которые предварительно генерируются в MS Excel; 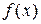– плотность вероятности искомых псевдослучайных чисел.

В [ ] на стр. приведены формулы для получения чисел с наиболее часто встречающимися законами распределения.

При построении имитационных моделей систем массового обслуживания (СМО) наиболее часто используется показательный закон распределения, функция плотность вероятности которого имеет вид

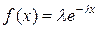. (4)

Экспоненциальная интегральная функция распределения имеет вид

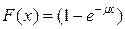, (5)

где 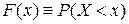– вероятность того события, что текущее значение переменной Х не превосходит фиксированное число (реализацию) х случайной величины.

Для того, чтобы получить выборку псевдослучайных чисел 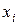с заданным законом распределения можно использовать метод обратной функции[1]. Для получения чисел 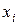с показательным законом распределения можно использовать формулу

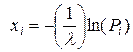, (6)

где - 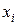- случайные числа, имеющие показательный закон распределения, 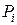- равномерно распределенные случайные числа.

Некоторые законы распределения можно смоделировать в Excel при помощи встроенных функций. Например, чтобы получить значение случайной величины, распределенной по нормальному закону с математическим ожиданием 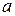и стандартным отклонением 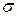можно воспользоваться строенной функцией НОРМОБР().

Для получения выборок псевдослучайных чисел в Excel можно воспользоваться инструментом Анализ данных / Генерация случайных чисел (пункт меню Сервис или Данные, в зависимости от версии MS Excel) (см. рисунок 3).

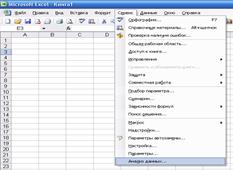
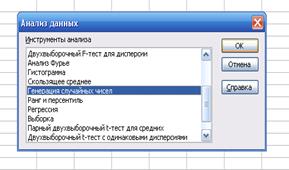
Рис. 3. Вызов модуля "Генерация случайных чисел" в Excel.

На экране появится диалоговое окно модуля "Генерация случайных чисел". В Excel предусмотрена возможность получения выборок псевдослучайных чисел, имеющих различные законы распределения. Пользователю необходимо указать количество случайных величин, объем генерируемой выборки, выбрать нужный закон распределения и указать параметры распределения. На рисунке 4 показан процесс получения выборки случайных чисел с нормальным законом распределения.

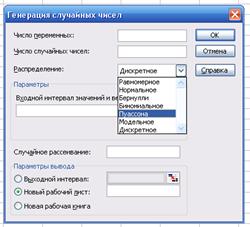
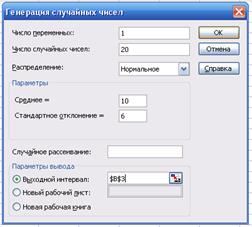
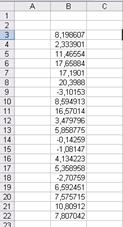
Рис. 4. Получение псевдослучайных чисел с нормальным законом распределения.

Более подробно о генерации случайных чисел в Excel можно прочесть в [1] или в литературе, посвященной использованию табличного процессора Excel.

Системы массового обслуживания. Основные понятия и определения.

Cистемой массового обслуживания (СМО), можно считать систему, в которой, с одной стороны, постоянно возникают запросы на выполнение каких-либо работ, а с другой — происходит постоянное удовлетво­рение этих запросов.

Требованием (клиентом, заявкой) в СМО называется каждый отдельный запрос на выполнение какой-либо работы.

Объект, выполняющий обслуживание требований, называется обслуживающим устройством или каналом обслуживания.

Временем обслуживания называется период, в течение которого удовлетворяется требование на обслуживание, т.е. период от начала обслуживания до его завершения.

Если к моменту поступления очередного требования все каналы обслуживания заняты, то требование попадает в очередь. Общее время пребывания завки в системе складывается из времени обслуживания и времени, проведенного в очереди.

Примеры систем массового обслуживания, встречающиеся нам в повседневной жизни, приведены в таблице 1.

Таблица 1. Примеры систем массового обслуживания.

Система массового обслуживания (СМО)	Каналы обслуживания	Требования (заявки)
Магазины	Продавцы (кассиры)	Покупатели
Справочная	Оператор	Клиенты
Билетная касса	Кассир	Пассажиры
Банк	Банкомат (оператор)	Клиенты банка
Парикмахерская	Мастера	Клиенты

СМО можно классифицировать по разным признакам.

По числу каналов обслуживания СМО делятся на:

· одноканальные

· много­канальные

В зависимости от условий ожидания начала обслу­живания различают СМО:

· с потерями (с отказами)

· с ожиданием (с очередью)

· смешанного типа

В СМО с отказами заявки, поступившие в момент, когда все каналы обслуживания заняты, получают отказ. Основной характеристикой эффек­тивности СМО с отказами является вероятность отказа в обслуживании.

В СМО с ожиданием заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь. Примером системы с ожиданием может быть касса в супермаркете. Для СМО с ожиданием основными характеристиками являются математическое ожидания длины очереди, среднее времени ожидания, коэффициент загруженности канала.

Встречаются также СМО смешанного типа. Для них характерно наличие некоторых дополнительных условий, например, ограничение на длину очереди.

По дисциплине обслуживания СМО делятся на

· СМО с приоритетом в обслуживании (заявки обслуживаются в порядке их поступления);

· СМО без приоритета в обслуживании (заявки обслуживаются в соответствии с установленными приоритетами, например, некоторая категория клиентов в магазине может обслуживаться без очереди).

По месту нахождения источника требований СМО делятся на

· разомкнутые (источник заявок на обслуживание находится вне системы, и число заявок теоретически бесконечно);

· замкнутые (когда источник находится в самой системе, число заявок ограничено).

Примером разомкнутых СМО являются магазины, кассы, банки. Примером замкнутой СМО может быть автомастерская, обслуживающая транспортный парк только одного предприятия.

Чаще всего СМО встречаются в торговле и в сфере бытового обслуживания населения. Для того, чтобы повысить эффективность работы, необходимо определить оптимальные параметры функционирования этих предприятий. Чаще всего оптимизируется количество каналов обслуживания.

Существуют аналитические и статистические методы исследования СМО.

Аналитические методы позволяют получить характеристики сис­темы как некоторые функции от параметров ее функционирования. Однако, аналитическому решению поддается лишь довольно ограниченный круг задач теории массового обслуживания.

Важнейшими параметрами любой СМО являются частота (интенсивоность) поступления заявок на обслуживание и время обслуживания заявок. Ни частота поступления заявок, ни время обслуживания заранее не известны, и поэтому эти характеристики рассматриваются как случайные величины, которые могут иметь зарличные законы распределения.

Лучше всего изучены и чаще применяются на практике модели СМО, в которых частота поступления заявок на обслуживание имеет закон распределения Пуассона (так называемый простейший поток), а время обслуживания распределено по экспоненциальному закону.

Для простейшего потока частота поступления заявок в сис­тему подчиняется закону Пуассона, т.е. вероятность поступления за время t ровно k требований задается формулой

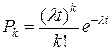, (7)

где 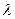- параметр, называемый интенсивностью входящего потока заявок.

Простейший поток обладает тремя основными свойствами:

· ординарность — это свойство означает, невозможность одновременного поступления двух и более требований за один и тот же интервал времени t. Например, если частота телефонных звонков на определенный номер имеет закон распределения Пуассона, то вероятность того, что за одну минуту на этот номер поступит более одного вызова очень мала;

· стационарность — математическое ожидание числа требо­ваний, поступающих в систему в единицу времени (обозначим че­рез X), не меняется во времени. Таким образом, вероятность по­ступления в систему определенного количества требований в тече­ние заданного промежутка времени 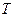зависит от его величины и не зависит от начала его отсчета на оси времени. Если рассматривать в качестве СМО работу магазина, то среднее число покупателей приходящих в магазин в течении часа, должно быть одинаково и утром, и днем, и вечером, что не всегда соответствует действительности;

· отсутствие последействия — число требований, поступив­ших в систему за период времени 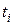, не зависит от того, сколько требова­ний поступило в систему в предшествующий период времени .

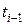Время обслуживания 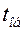заявок является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории, и особенно в практических приложениях, получил экспоненциальный закон. Для этого закона функция распределения вероятностей имеет вид

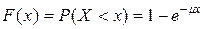, (8)

где 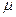— пара­метр экспоненциального закона распределения. Величину 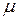называют интенсивностью обслуживания заявок, и она обратно пропорциональна среднему времени обслуживания 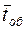, т.е. .

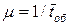Типовая постановка задачи, решаемой с помощью теории массо­вого обслуживания, состоит в следующем: зная закон распределения частоты поступления заявок и закон распределения времени обслуживания нуж­но оценить качество и эффективность функционирования СМО и выявить возможность для их улучшения.

Рассмотрим n-канальную СМО с отказами. Входящий поток заявок имеет показательный закон распределения с интенсивностью 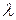, а время обслуживания подчиняется экспоненциальному закону, интенсивность обслуживания 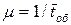. Заявка, заставшая систему занятой, сразу же покидает ее.

Следует определить: вероятность того, что заявка, пришедшая в момент времени t, получит отказ; абсолютную и относительную пропускную способность СМО; среднее число занятых каналов.

Это одна из немногих задач теории массового обслуживания, для которой существует аналитическое решение. Ниже приведены формулы, при помощи которых можно оценить основные характеристики работы такой СМО.

Вероятность отказа в обслуживании (вероятность того, что все n каналов заняты)

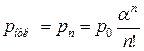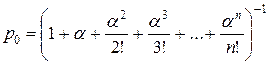, , (9)

где 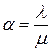- нагрузка на систему.

Относительная пропускная способность, то есть вероятность того, что заявка будет принята к обслуживанию

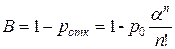. (10)

Абсолютная пропускная способность (количество обслуженных заявок за некоторый период времени)

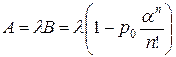. (11)

Среднее число занятых каналов

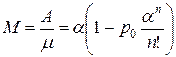. (12)

Пример 1. В холле крупного торгового центра стоят 2 терминала оплаты. Будем считать, что входящий поток требования является простейшим, а среднее число покупателей, желающих воспользоваться терминалами, составляет 15 человек в час. Время обслуживания клиентов имеет экспоненциальный закон распределения, среднее время обслуживания одного клиента равно 3 минуты.

Необходимо оценить основные характеристики работы данной СМО.

Решение. Интенсивность поступления заявок и время обслуживания необходимо привести к одному временному интервалу. За единицу времени примем 1 час. Тогда 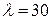чел/час, 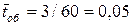часа, 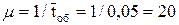. Нагрузка на систему .

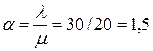Найдем вероятность отказа в обслуживании по формуле (3) для 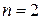. Результаты вычислений округлим до сотых.

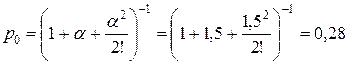
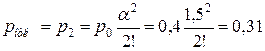
Относительная пропускная способность СМО, т.е. вероятность того, что очередная заявка будет обслужена, составляет

.

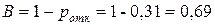Абсолютная пропускная способность (количество обслуженных заявок в течение часа)

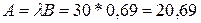
Среднее число занятых каналов

.

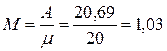Полученные результаты говорят о том, что данная СМО работает неэффективно, т.к. обслуживается только около 70% поступивших требований, а 30% получают отказ, что ведет к снижению выручки владельца терминалов. Очевидно, что повысить эффективность работы можно либо увеличив число каналов обслуживания либо уменьшив среднее время обслуживания. В данном случае повлиять на среднее время обслуживания невозможно, и остается только увеличивать количество терминалов.

В таблице 2 приведены значения основных характеристик СМО для разного количества каналов обслуживания, а на рисунке 5 – график вероятности отказа в обслуживании.

Таблица 2. Основные характеристики работы СМО.

Кол-во терминалов,	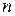Вероятность отказа,	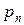Относительная пропускная способность,	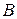Абсолютная пропускная способность,	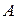Среднее число занятых каналов,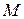
	0,60	0,40	12,00	0,60
	0,31	0,69	20,69	1,03
	0,13	0,87	25,97	1,30
	0,05	0,95	28,56	1,43
	0,01	0,99	29,57	1,48
	0,00	1,00	29,89	1,49
	0,00	1,00	29,98	1,50
	0,00	1,00	30,00	1,50
	0,00	1,00	30,00	1,50
	0,00	1,00	30,00	1,50

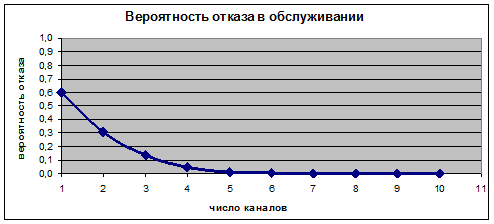
Рис. 5. График вероятности отказа в обслуживании.

Из таблицы и рисунка видно, что при увеличении числа каналов обслуживания на единицу ( 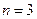) вероятность отказа снизится до 0,13, а абсолютная пропускная способность составит 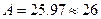, т.е. из 30 заявок, поступающих в течение часа, только 4 получат отказ. Дальнейшее увеличение числа каналов позволит еще сократить количество отказов, однако это связано с дополнительными затратами (покупка новых терминалов). Какое же число каналов будет оптимальным для данной системы?

Чтобы ответить на этот вопрос, необходимо учесть ряд экономических показателей, таких как стоимость нового терминала, средняя величина потерь, вызванных отказом в обслуживании, срок окупаемости дополнительного оборудования и т. п. При анализе СМО часто используются функции стоимости потерь. Для СМО с отказами:

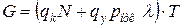, (13)

где 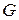- функция стоимости потерь за период времени 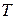; 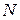- среднее число простаивающих каналов; 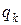- стоимость единицы времени простоя канала обслуживания; 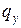- величина потерь, вызванных отказом в обслуживании одной заявки; 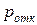- вероятность отказа в обслуживании (при фиксированном значении 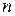); 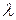- интенсивность входящего потока заявок.

Для СМО с очередью:

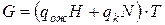, (14)

где 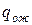- оценка величины потерь, вызванных нахождением заявки в очереди в единицу времени; 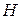- средняя длина очереди в системе.

Вычислим функцию стоимости потерь 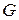для примера 1 по формуле (13). Оценим величину потенциальных убытков, вызванных отказом в обслуживании за 1 год. За единицу времени в задаче принят 1 час. Пусть торговый центр, в котором стоят терминалы, работает без выходных дней, 14 часов в сутки. Тогда интервал 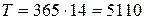рабочих часов в год. Среднее число простаивающих каналов 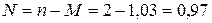. Потери, связанные с простоем канала обслуживания отсутствуют, т.е. .

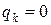Пусть средний платеж на терминале оплаты - 100 руб., при этом комиссия владельца терминала составляет 2%. То есть каждая обслуженная заявка приносит владельцу в среднем 2 руб. Тогда величина потерь, связанная с отказом в обслуживании 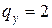. Вероятность отказа в обслуживании (для 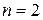) равна 0,31, интенсивность потока заявок 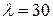. Тогда 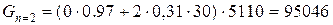рублей в год.

Предположим, что покупка нового терминала с доставкой и установкой обойдется в 80000 рублей, и аренда места под терминал составит еще 20000 руб. в год. Итого 100000 руб. дополнительных затрат. За какой срок они окупятся? При 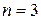, вероятность отказа в обслуживании 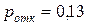, а значение функции потерь составит 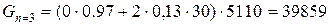рублей. То есть покупка терминала позволит уменьшить потери, вызванные отказом в обслуживании на 95046-39859=55187 руб. в год. Таким образом, затраты на покупку нового терминала окупятся примерно за 2 года.