Нормальный закон распределения

Нормальный закон распределения играет исключительную роль в теории вероятностей. Это наиболее часто встречающийся закон распределения, главной особенностью которого является то, что он является предельным законом, к которому, при определенных условиях, приближаются другие законы распределения.

Если представляется возможным рассматривать случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения, но при этом должно выполняться условие их независимости (или слабой зависимости). Ни одна из суммируемых случайных величин не должна резко отличаться от других и не должна иметь исключительно большую дисперсию по сравнению с другими дисперсиями.

Пример. Отклонения размеров изготовленных деталей от стандарта.

Непрерывная случайная величина X имеет нормальное распределение, если плотность распределения вероятности имеет вид

,

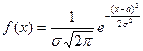где a и σ параметры распределения.

Математическое ожидание M(x) = a характеризует центр распределения, а дисперсия D(x) = σ² - форму распределения.

Вероятность попадания нормального распределенной случайной величины в заданный интервал определяется следующим образом:

,

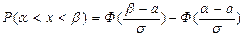где 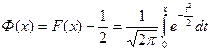называется функцией Лапласа.

Функция Лапласа Ф(x) – нечетная функция. Значения функции Лапласа можно найти в соответствующей таблице (приложение 1).

Если случайная величина X имеет нормальное распределение, то отклонение этой случайной величины от ее математического ожидания по абсолютной величине не превышает утроенное среднее квадратичное отклонение 3σ (правило 3σ, вероятность Р = 0,997, т.е. она приблизительно равна 1). На этом правиле основана оценка σ. Из полученных данных наблюдения случайной величины выбирают максимальное и минимальное значения и их разность делят на 6.

Вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине составляет 2σ, равна 0,954, а вероятность того, что это отклонение составляет σ, равна 0,683.

@ Задача 2: Вес вылавливаемых в пруду рыб подчиняется нормальному закону распределения со средним квадратичным отклонением 150г и математическим ожиданием а = 1000г. Найти вероятность того, что вес пойманной рыбы будет: а) от 900 до 1300г; б) не более 1500г; в) не менее 800г; г) отличаться от среднего веса по модулю не более чем на 200г.

Решение:

а) P(900 < x < 1300) = Ф(2) – Ф(– 0,67) = 0,48 + 0,25 = 0,73;

б) P(0 < x < 1500) = Ф(3,3) – Ф(– 6,6) = 0,4996 + 0,4999 = 0,9995;

в) P(800 < x < ¥) = Ф(¥) – Ф(– 1,33) = 0,5 + 0,41 = 0,91;

г) P(800 < x < 1200) = Ф(1,33) – Ф(– 1,33) = 0,41 + 0,41 = 0,82.

Основные теоремы теории вероятности