Функции крылова и их свойства

Функции Крылова - система из четырёх функций, представляющих собой общее решение дифференциального уравнения колебаний: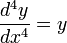

Функции Крылова выражаются следующим образом: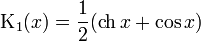

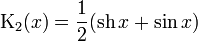
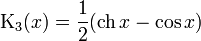
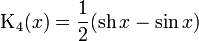
Основное свойство функций Крылова в том, что производная от любой из них даёт какую–нибудь другую из этих же функций:

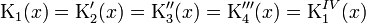Функции Крылова используются в задачах теории упругости.

Значительно более сложным оказывается решение для коротких балок, когда требуется учесть условия на обоих концах балки. К таким балкам относится, например, рельсовый путь на шпалах (рис.17.8). Для коротких балок нельзя использовать решения, полученные для балок бесконечной длины и требуется исходить из общего интеграла (17.9), содержащего четыре произвольные постоянные интегрирования. Для решения обычно пользуются нормальными фундаментальными функциями уравнения (17.5). Эти функции называемые функциями Крылова, являются решениями однородного уравнения (17.5) и удовлетворяют специальным условиям при x = 0. Cоставим следующую таблицу, в которой сведены начальные значения функций Крылова и их производных:

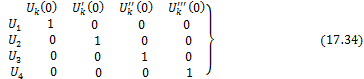
Так как во всех клетках этой таблицы стоят нули, лишь на главной диагонали единицы, то система частных решений U_k , называется системой с единичной матрицей. Эти решения суть:

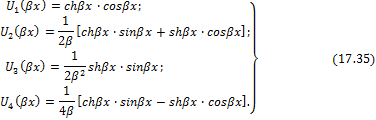
Следует отметить, что производные функций Крылова (17.35) выражаются снова через те же функции, причем:

Таким образом, общий интеграл уравнения (17.9) может быть представлен через функции Крылова:

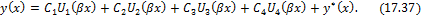
Постоянные интегрирования C₁ , C₂ , C₃ , C₄ имеют здесь со­вершенно определенный смысл. Действительно, если положить x = 0, и воспользоваться свойством (17.34) введенных функций, получим:

Таким образом:

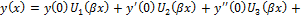
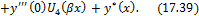Формула (17.39) представляет общий интеграл уравнения (17.5). Постоянные интегрирования имеют здесь простой смысл: это на­чальные (при x = 0) значения искомой функции и ее производные. Поэтому, метод интегрирования дифференциальных уравнений, основанный на формуле (17.39), и широко применяемый в строительной механике, называетсяметодом начальных параметров.Согласно метода начальных параметров, балка разбивается на участки. Подставив (17.38) в (17.39), получим функцию прогибов на I участке балки:

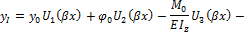
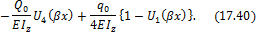Пользуясь приведенными в (17.36) правилами дифференцирования от функций прогибов (17.40) переходим к углам поворота 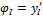и далее по формулам (17.25), (17.26) к внутренним усилиям на I участке:

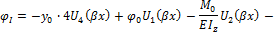
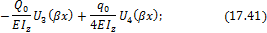
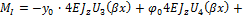
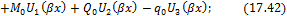
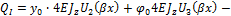
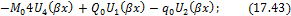
Функцию 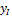продолжаем на второй и последующие участки. Приращения 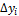этой функции будут зависеть от приращений внутренних сил 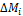, 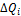и интенсивности нагрузки на границах между участками 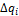. Добавляя эти приращения к функции прогибов, углов поворота, изгибающих моментов и поперечных сил, получим универсальные формулы:

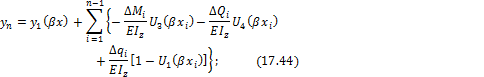
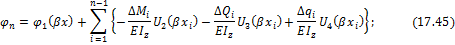
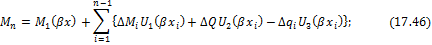
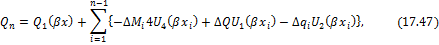
здесь для краткости обозначено 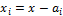; 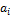- абсцисса i-ой границы между участками.

Как и в обычной балке, в начале координат часть начальных параметров бывает известна, а остальные определяются из гранич­ных условий, формируемых для противоположного конца стержня.

С целью облегчения вычислений при выполнении практических расчетов балок на упругом основании в таблице 17.7 приводят­ся значения тригонометрических, гиперболических функций и функций Крылова при заданном аргументе.

Закон Гука

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствиеэлектромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

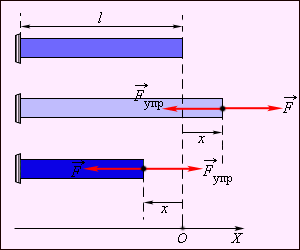Рисунок 1.12.1. Деформация растяжения (x > 0) и сжатия (x < 0). Внешняя сила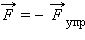

Простейшим видом деформации являются деформации растяжения и сжатия (рис. 1.12.1).

При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации: Fx = Fупр = –kx.

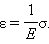Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / lназывается относительной деформацией, а отношение σ = F / S = –F_упр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ:

Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·10¹¹ Н/м², а для резины E ≈ 2·10⁶ Н/м², т. е. на пять порядков меньше.

Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах.

Деформация изгиба.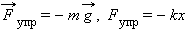

Упругую силу 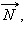действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести: 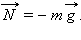Сила 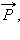с которой тело действует на стол, называется весом тела.

Деформация растяжения пружины.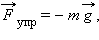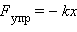

В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.

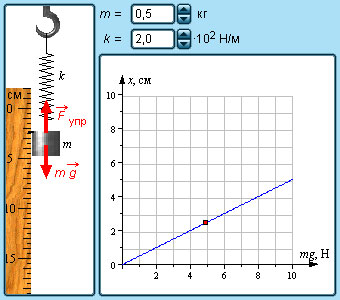Модель. Закон Гука