Метод множителей Лагранжа

Рассмотрим частный случай общей задачи НЛП.

Предполагая, что сумма ограничений 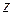содержит только уравнения, отсутствуют условия неотрицательности переменных и функции 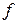, а так же 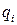функции непрерывные вместе со своими частными производными (это классическая задача оптимизации):

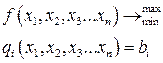
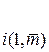
Что бы найти решение этой задачи водят набор переменных 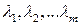называются множителями Лагранжа, тогда функция Лагранжа:

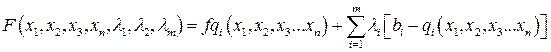
Далее находят все частные производные функции Лагранжа

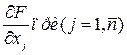и

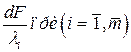
Затем рассматриваем систему 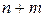уравнений с 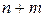неизвестными

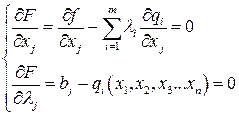
Решив систему уравнений получают все точки, в которых функция 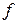может иметь экстремальные значения. Дальнейшее исследование найденных точек производят так же, как и в случае безусловного экстремума.

Пример. Найти точки экстремума функции

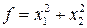при условиях

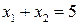
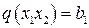
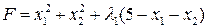
З переменных:

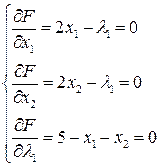
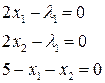
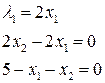
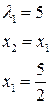
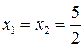
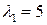
Таким образом, в точке 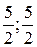данная функция может иметь условный экстремум

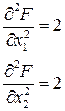
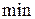
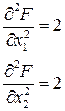
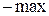
Используя вторые частные производные можно показать, что в этой точке функция имеет условный минимум и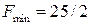

Метод множителей Лагранжа можно применять и когда условие связи представляет собой неравенство. Если нужно найти экстремум функци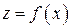и при 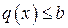, то следует сначала найти точки безусловного экстремума функций из уравнений производных .

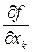Затем, среди этих точек отобрать те, координаты которых удовлетворяют условию связи 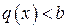, а так же определить точки, удовл. системе уравнений

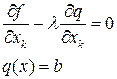
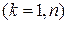
Точки, найденные в результате решения системы вместе с точками определенными на І этапе, а также удовлетворяя условиям 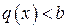подлежат дальнейшему исследованию как и при нахождение безусловного экстремума. Особым классом задач ИО являются задачи выпуклого программирования для которых разработано много эффективных решений.

Задача является задачей выпуклого программирования, если целевая функция будет либо выпуклой, либо вогнутой.

К методам решения задач ВП относят:

· метод Франка - Вульфа;

· метод штрафных функций;

· метод Эрроу – Гурвица;

Эти методы являются градиентными методами и методы использования сепарабельные функции:

· функция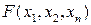

Функция сепарабельная, если она может быть представлена в виде суммы функции, каждая из которых является функцией одной переменной

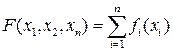
Если целевая функция и функции в системе ограничений – сеперабельное то приблизительно решение такой задачи можно найти используя кусочно – линейную аппроксимацию.

Пример: Джек студент – первокурсник, он пришел к выводу, что одна только учеба без ежедневной игры в баскетбол плохо влияет на его умственное, моральное и физическое развитие, поэтому он решил распределить своё время примерно 10 часов для учебы и игры в баскетбол. Привлекательность игрового времени он оценивает в два раза больше чем привлекательность времени затраченного на учебу. Но имея совесть и чувство долга Джек решил что время для игры не превышает времени на учебу, кроме того он заметил что если выполнять все учебные задания, на игру останется не более 4 часов в день. Распределить время так что бы Джек получал максимальное удовольствие от игры и от работы.

х₁ – время на игру

х₂ – время на учебу

х₁ + х₂ ≤ 10

х₁ ≤ х₂

х₁ ≤ 4

х₁ + х₂ + S₁ = 10

х₁ - х₂ + S₁ = 0

х₁ + S₁ = 4

z = 2х₁ + х₂

Базис	z	х2	х2	S1	S2	S3	Реш.
z			-1
S1							10 10
S2			-1				0 0
S3							4 4

z			-3
S1					-1		10 5
x1			-1				0 -0
S3					-1		4 4

z					-1
S1						-2	2 2
x1							4 ∞
x2					-1		4 -4

Базис	z	х1	х2	S1	S2	S3	Реш.
z
S2						-2
x1
x2						-1

x₁ = 4

x₂ = 6

z = 14

Задачи ЛП и НЛП решаются за 1 шаг. Такие задачи называются одношаговыми (однотипные). Задачи Дин. Пр. называются многошаговыми – на каждом шаге определяется решение некой частей задачи обусловленной исходной задачей.

Общая постановка задачи ДП. Пусть некоторая физическая система S находится в некотором начальном состоянии S₀ Є Sнач. и является управляемой. Благодаря некоторому упр. U данная система переходит из начального состояния S₀ в конечное состояние Sкон., Sкон Є Sк.

При этом качестве каждого из управлений U характеризуется соответствующим значением функции W(U).

Задача состоит в том чтобы из множества управлений найти такое, при котором функция W(U) принимает экстремальное значение.

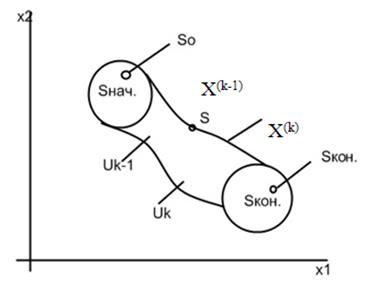
Решение задач ДП осуществляется по схеме:

Будем считать, что состояние рассматриваемой системы S на каком то k^-m шаге, причем k = 1…n определяется совокупностью чисел Х^(k) = (x₁^(k), x₂^(k), … x_n^(k)), которые получены в результате реализации управления Uk, обеспечивающего переход системы Sиз состояния Х^(k-1) в состояние Х^(k).

При этом считается что состояние Х^(k) зависит от состояния Х^(k-1) и выбранного управления Uk, но не зависит от того каким образом система S перешла в это состояние.

Врез. реализации К-го шага был получен выигрыш состояния зависящий от пред. состояния (Х(k-1)) и уравнения Uk.

Общий вклад при этом будет составлять:

n

F = ∑ Wk (Х(k-1), Uk)

k=1

Решения задач ДП по подобной схеме осуществляется в рамках принципа оптимальности Беллмона.

Формулировка: каково бы не было состояние системы перед очередным шагом надо на следующем шаге выбирать управление так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимален.