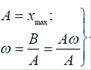Объект без самовыравнивания. Расшифровка методов ПИ ПИД
Расшифровка методов
 |  |  | |
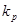| ПИ |  |  | |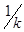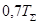
| ПИД |  |  |  |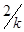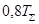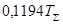
Расчет настроек регулятора методом Куна (нормальная настройка)
Расчет настроек регулятора методом Куна (быстрая настройка)
Расчет настроек регулятора по Копеловичу
| Регулятор | Типовой процесс регулирования | ||
| апериодический | с 20% перерегулир |  | |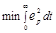
| П |  |  | – |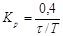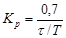
| ПИ |  |   |   |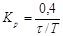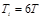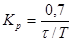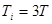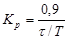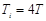
| ПИД |    |    |    |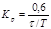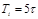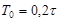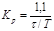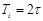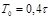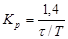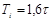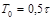
| Регулятор | Типовой процесс регулирования | ||
| апериодич | с 20% перерегулир |  | |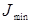
| И |  |  |  |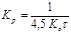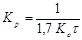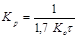
| П |  |  |  |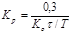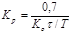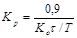
| ПИ |   |   |  |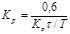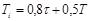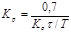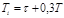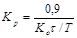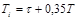
| ПИД |    |    |    |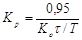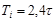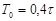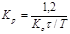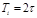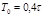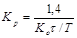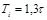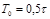
объект с самовыравниванием
объект без самовыравнивания
Формулы метода ВТИ (Всесоюзный технологический институт)
 | |||
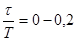| Параметр закон регул. | П | ПИ | ПИД |
| Кр |  |  |  |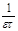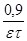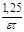
| Ти | – |  |  |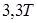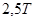
| То | – | – |  |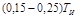
| Тим |  |  |  |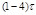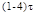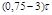
 | |||
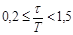| П | ПИ | ПИД | |
| Кр |  |  |  |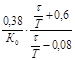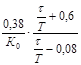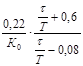
| Ти | – |  |  |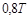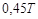
| То | – | – |  |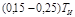
| Тим |  |  |  |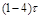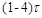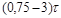
| Отношение запаздывания объекта к его пост. времени |  | ||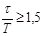
| Параметр закон регул. | П | ПИ | ПИД |
| Кр |  |  |  |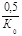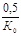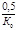
| Ти | – |  |  |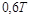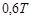
| То | – | – |  |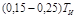
| Тим |  |  |  |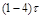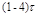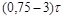
5. Автоколебания в САР. Определение параметров автоколебаний с помощью графических построений.
В нелинейных САР возможны собственные колебания с постоянной амплитудой частотой при отсутствии внешних колебательных воздействий. Эти колебания могут быть устойчивыми и неустойчивыми. Устойчивые собственные колебания с постоянной амплитудой и частотой при отсутствии внешних колебательных воздействий называются автоколебаниями. Удобно рассматривать эти собственные колебания, привлекая фазовую плоскость, по осям которой откладываются координаты х – отклонение выходной
переменной системы от установившегося значения и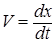 
- скорость изменения этого отклонения.
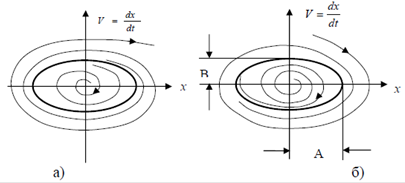
Жирной линией на фазовой плоскости обозначены особые линии – для
а) устойчивого, б) неустойчивого предельного циклов.
Предельные циклы разграничивают области начальных условий, для которых фазовые траектории носят качественно разный характер. Так, для а), фазовые траектории для начальных условий, находящихся внутри предельного цикла, раскручиваются от положения равновесия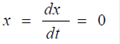 
до предельного цикла, а для начальных условий, находящихся вне предельного цикла, - скручиваются извне до предельного цикла. Значит, в такой нелинейной системе нет состояния устойчивого равновесия, а есть режим автоколебаний. Для случая б) картина противоположная, здесь для области начальных условий, расположенных внутри предельного цикла, имеет место положение устойчивого равновесия в начале координат, а предельный цикл характеризует неустойчивые собственные колебания.
Если в системе установились гармонические автоколебания, то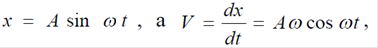 
где А – амплитуда, а ω – частица гармонических колебаний. Максимальные значения для х будет при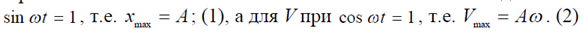 
На фазовой плоскости значения амплитуды и частоты автоколебаний непосредственно не просматриваются. Однако, их можно определить приблизительно, исходя из рассмотрения предельного цикла. Если предельный цикл не является эталоном, то автоколебания не будут гармоническими колебаниями. Если, однако, положить, что автоколебания будут близки к гармоническим, то из картинки предельного цикла а) имеем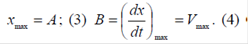 
Сравнивая (1) и (3), (2) и (4) имеем для амплитуды и частоты автоколебаний: 