Свойства простых чисел
1) Всякое натуральное число, большее 1, делится по крайней мере на одно простое число.
Доказательство: Пусть 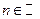 и
и 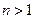 . Если п - простое, то все доказано, т.к.
. Если п - простое, то все доказано, т.к. 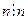 .
.
Если п - составное, то п делится на число 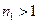 , меньшее, чем п. Если
, меньшее, чем п. Если 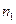 - простое, то свойство доказано:
- простое, то свойство доказано: 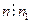 . Если
. Если 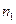 - составное, то
- составное, то 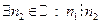 и
и 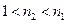 и т.д.
и т.д.
Процесс выделения делителей 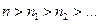 оборвется через конечное число шагов, когда мы придем к простому делителю. ▲.
оборвется через конечное число шагов, когда мы придем к простому делителю. ▲.
2) Любое целое число или делится на простое число р, или взаимно просто с ним.
Доказательство: Пусть а - целое число; обозначим 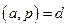 . Так как
. Так как 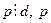 - простое, то или
- простое, то или 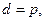 а тогда
а тогда 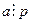 , или
, или 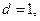 а тогда а и р взаимно просты. ▲.
а тогда а и р взаимно просты. ▲.
3) Два различных простых числа взаимно просты.

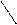 Доказательство: Пусть
Доказательство: Пусть 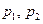 - простые и
- простые и 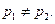 Для определенности пусть
Для определенности пусть 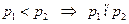 (докажем это от противного – пусть
(докажем это от противного – пусть 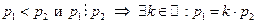 и т.к.
и т.к. 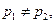 то
то 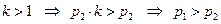 , ).
, ). 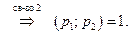 ▲.
▲.
4) Если произведение двух целых чисел делится на простое число, то хотя бы один из сомножителей делится на это простое число.
Доказательство: Пусть 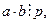 р – простое число,
р – простое число, 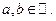
Если 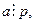 то всё доказано. Если
то всё доказано. Если 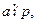 то по свойству 2,
то по свойству 2, 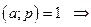 по свойствам взаимно простых чисел
по свойствам взаимно простых чисел 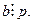 ▲.
▲.
Замечание: использовано следующее свойство взаимно простых чисел:
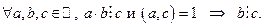
Доказательство: 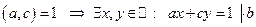
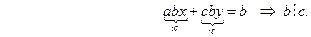 ▲.
▲.
Следствие: Если произведение нескольких чисел делится на простое число р, то хотя бы один из сомножителей делится на это число р. (доказательство методом математической индукции по числу п сомножителей).
Теорема 1. (ОСНОВНАЯ ТЕОРЕМА АРИФМЕТИКИ).Всякое натуральное число, большее 1, может быть представлено в виде произведения простых сомножителей и два таких разложения могут отличаться только порядком следования сомножителей.
Доказательство: 1. Возможность указанного представления. Применим метод математической индукции.
1) Для числа 2 утверждение теоремы тривиально.
2) Допустим, что теорема верна для всех натуральных чисел, меньших п.
3) Докажем теорему для числа п. Если п - простое число, то всё доказано.
Если п - составное число, то 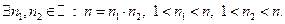 Тогда в силу индуктивного предположения
Тогда в силу индуктивного предположения 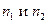 допускают разложение на простые множители:
допускают разложение на простые множители: 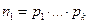
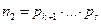
Тогда 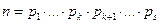 и возможность разложения числа п доказана.
и возможность разложения числа п доказана.
2. Однозначность разложения. Для доказательства однозначности разложения с точностью до порядка следования сомножителей также применим метод математической индукции.
1) Для числа 2 утверждение справедливо, т.к. 2 – простое число.
2) Допустим, что утверждение верно для всех натуральных чисел, меньших п.
3) Докажем утверждение для числа п. Допустим, что п двумя способами разложено в произведение простых сомножителей: 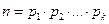 и
и 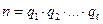 , где
, где 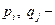 простые числа
простые числа 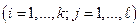 .
.
Тогда 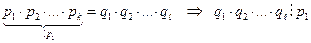
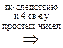 один из сомножителей произведения
один из сомножителей произведения 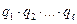 делится на
делится на 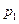 .
.
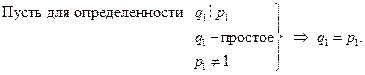
Тогда 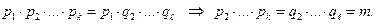 Но число
Но число 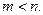 Тогда по индуктивному предположению для т утверждение справедливо, т.е. два разложения числа т могут отличаться только порядком следования сомножителей. Следовательно,
Тогда по индуктивному предположению для т утверждение справедливо, т.е. два разложения числа т могут отличаться только порядком следования сомножителей. Следовательно, 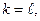 простые числа
простые числа 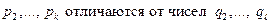 только порядком следования. Значит утверждение верно и для числа п.
только порядком следования. Значит утверждение верно и для числа п.
Итак, по методу математической индукции утверждение верно для любого натурального числа, большего 1. ▲.
Замечание: Среди сомножителей в разложении 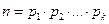 могут быть равные. Их произведение принято записывать в виде степеней. Пусть
могут быть равные. Их произведение принято записывать в виде степеней. Пусть 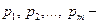 различные простые сомножители числа п и число
различные простые сомножители числа п и число 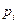 входит в разложение числа п
входит в разложение числа п 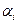 раз
раз 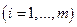 , тогда число п можно записать в виде:
, тогда число п можно записать в виде: 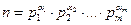 . Такое разложение называется каноническим разложением числа п.
. Такое разложение называется каноническим разложением числа п.
Пример: Найдем каноническое разложение числа 1176.
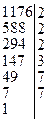 Значит
Значит