Критерии поверки статистических гипотез. Критерии Пирсона и Романовского
Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими.
Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза.
Различают простые и сложные гипотезы. Гипотезу называют простой, если она однозначно характеризует параметр распределения случайной величины. Например, если l является параметром экспоненциального распределения, то гипотеза Н0 о равенстве l=10 – простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н0 о неравенстве l>10 состоит из бесконечного множества простых гипотез Н0 о равенстве l=bi, где bi – любое число, большее 10. Гипотеза Н0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии.
Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z=z(x1, x2, …, xn). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S0 и S1. Если значение критерия z попадает в область S0, то гипотеза принимается, а если в область S1, то гипотеза отклоняется. Множество S0 называется областью принятия гипотезы или областью допустимых значений, а множество S1 – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область.
Принятие или отклонение гипотезы Н0 по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок. Ошибка первого рода возникает с вероятностью a тогда, когда отвергается верная гипотеза Н0 и принимается конкурирующая гипотеза Н1. Ошибка второго рода возникает с вероятностью b в том случае, когда принимается неверная гипотеза Н0, в то время как справедлива конкурирующая гипотеза Н1. Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н0. Вероятность отвергнуть ложную гипотезу Н0 называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре варианта исходов, табл.
Таблица
| Гипотеза Н0 | Решение | Вероятность | Примечание |
| Верна | Принимается | 1 - a | Доверительная вероятность |
| Отвергается | a | Вероятность ошибки первого рода | |
| Неверна | Принимается | b | Вероятность ошибки второго рода |
| Отвергается | 1 - b | Мощность критерия |
Например, рассмотрим случай, когда некоторая несмещенная оценка параметра q вычислена по выборке объема n, и эта оценка имеет плотность распределения f(q), рис. 1.
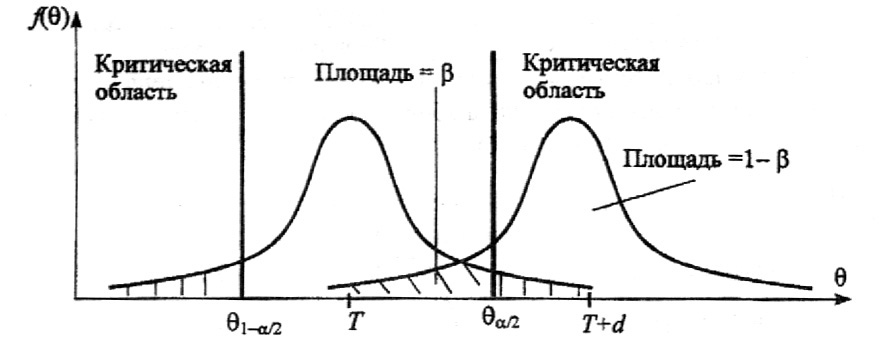
Рис. 1. Области принятия и отклонения гипотезы
Предположим, что истинное значение оцениваемого параметра равно Т. Если рассматривать гипотезу Н0 о равенстве q=Т, то насколько велико должно быть различие между q и Т, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос можно в статистическом смысле, рассматривая вероятность достижения некоторой заданной разности между q и Т на основе выборочного распределения параметра q.
Целесообразно полагать одинаковыми значения вероятности выхода параметра q за нижний и верхний пределы интервала. Такое допущение во многих случаях позволяет минимизировать доверительный интервал, т.е. повысить мощность критерия проверки. Суммарная вероятность выхода параметра q за пределы интервала с границами q1–a/2 и qa/2, составляет величину a. Эту величину следует выбрать настолько малой, чтобы выход за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то в таком случае нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства q=Т можно принять. Но если после получения выборки окажется, что оценка выходит за установленные пределы, то в этом случае есть серьезные основания отвергнуть гипотезу Н0. Отсюда следует, что вероятность допустить ошибку первого рода равна a (равна уровню значимости критерия).
Если предположить, например, что истинное значение параметра в действительности равно Т+d , то согласно гипотезе Н0о равенстве q=Т – вероятность того, что оценка параметра q попадет в область принятия гипотезы, составит b, рис. 2.
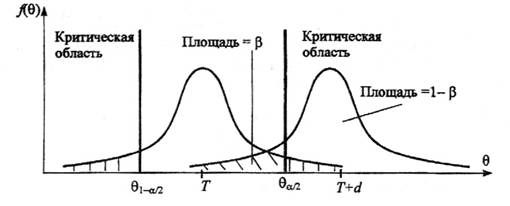
Рис. 2. Области принятия и отклонения гипотезы
При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости a. Однако при этом увеличивается вероятность ошибки второго рода b (снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т–d.
Единственный способ уменьшить обе вероятности состоит в увеличении объема выборки (плотность распределения оценки параметра при этом становится более "узкой"). При выборе критической области руководствуются правилом Неймана – Пирсона: следует так выбирать критическую область, чтобы вероятность a была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения a относительно произволен. Употребительные значения лежат в пределах от 0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы интервалов с границами q1–a/2 и qa/2 для типовых значений a и различных способов построения критерия.
При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия.
В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. К числу наиболее часто применяемых критериев для проверки гипотез о законах распределения относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о значениях параметров – критерии Фишера, Стьюдента.
Распределение хи-квадрат
Распределению хи-квадрат (c2-распределению) с k степенями свободы соответствует распределение суммы
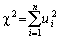 квадратов n стандартизованных случайных величин ui, каждая из которых распределена по нормальному закону, причем k из них независимы, n>=k. Функция плотности распределения хи-квадрат с k степенями свободы
квадратов n стандартизованных случайных величин ui, каждая из которых распределена по нормальному закону, причем k из них независимы, n>=k. Функция плотности распределения хи-квадрат с k степенями свободы
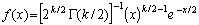 , x >= 0, , x >= 0, |
где х=c2, Г(k/2) – гамма-функция.
Число степеней свободы k определяет количество независимых слагаемых в выражении для c2. Функция плотности при k, равном одному или двум, – монотонная, а при k>2 – унимодальная, несимметричная, рис. 3
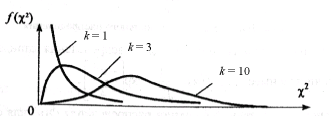
Рис. 3. Плотность распределения хи-квадрат
Математическое ожидание и дисперсия величины c2 равны соответственно k и 2k . Распределение хи-квадрат является частным случаем более общего гамма-распределения, а величина, равная корню квадратному из хи-квадрат с двумя степенями свободы, подчиняется распределению Рэлея.
С увеличением числа степеней свободы (k>30) распределение хи-квадрат приближается к нормальному распределению с математическим ожиданием k и дисперсией 2k. В таких случаях критическое значение
c2(k; a) » u1–a(k, 2k),
где u1–a(k, 2k) – квантиль нормального распределения. Погрешность аппроксимации не превышает нескольких процентов.
Распределение Стьюдента
Распределение Стьюдента (t-распределение, предложено в 1908 г. английским статистиком В. Госсетом, публиковавшим научные труды под псевдонимом Student) характеризует распределение случайной величины
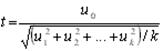
где u0, u1, …, uk взаимно независимые нормально распределенные случайные величины с нулевым средним и конечной дисперсией. Аргумент t не зависит от дисперсии слагаемых. Функция плотности распределения Стьюдента
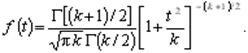 | (3.5) |
Величина k характеризует количество степеней свободы. Плотность распределения – унимодальная и симметричная функция, похожая на нормальное распределение, рис. 4.
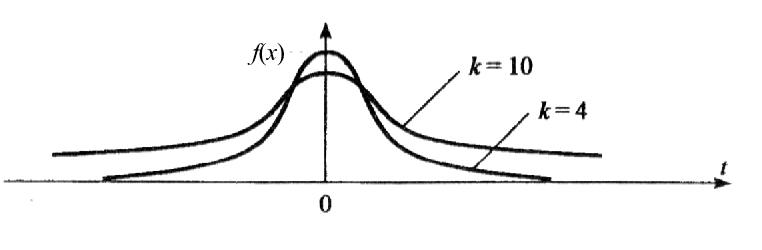
Рис. 4. Плотность распределения Стьюдента
Область изменения аргумента t от минус до плюс бесконечности. Математическое ожидание и дисперсия равны 0 и k/(k–2) соответственно, при k>2. По сравнению с нормальным распределение Стьюдента более пологое, оно имеет меньшую дисперсию. Это отличие заметно при небольших значениях k, что следует учитывать при проверке статистических гипотез (критические значения аргумента распределения Стьюдента превышают аналогичные показатели нормального распределения). Таблицы распределения содержат значения для односторонней (пределы интегрирования от r(k; a ) до бесконечности)
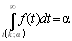 или двусторонней (пределы интегрирования от – r(k; a) до r(k; a))
или двусторонней (пределы интегрирования от – r(k; a) до r(k; a))
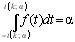 критической области. Распределение Стьюдента применяется для описания ошибок выборки при k<30. При k, превышающем 100, данное распределение практически соответствует нормальному, для значений k из диапазона от 30 до 100 различия между распределением Стьюдента и нормальным распределением составляют несколько процентов. Поэтому относительно оценки ошибок малыми считаются выборки объемом не более 30 единиц, большими – объемом более 100 единиц. При аппроксимации распределения Стьюдента нормальным распределением для односторонней критической области вероятность Р{t>t(k; a)} = u1–a(0, k /(k–2)), где u1–a(0, k/(k–2)) – квантиль нормального распределения. Аналогичное соотношение можно составить и для двусторонней критической области.
критической области. Распределение Стьюдента применяется для описания ошибок выборки при k<30. При k, превышающем 100, данное распределение практически соответствует нормальному, для значений k из диапазона от 30 до 100 различия между распределением Стьюдента и нормальным распределением составляют несколько процентов. Поэтому относительно оценки ошибок малыми считаются выборки объемом не более 30 единиц, большими – объемом более 100 единиц. При аппроксимации распределения Стьюдента нормальным распределением для односторонней критической области вероятность Р{t>t(k; a)} = u1–a(0, k /(k–2)), где u1–a(0, k/(k–2)) – квантиль нормального распределения. Аналогичное соотношение можно составить и для двусторонней критической области.
Критерий хи-квадрат К. Пирсона. Использование этого критерия основано на применении такой меры (статистики) расхождения между теоретическим F(x) и эмпирическим распределением Fп(x), которая приближенно подчиняется закону распределения c2. Гипотеза Н0 о согласованности распределений проверяется путем анализа распределения этой статистики. Применение критерия требует построения статистического ряда.
Итак, пусть выборка представлена статистическим рядом с количеством разрядов y. Наблюдаемая частота попаданий в i-й разряд ni. В соответствии с теоретическим законом распределения ожидаемая частота попаданий в i-й разряд составляет Fi. Разность между наблюдаемой и ожидаемой частотой составит величину (ni–Fi). Для нахождения общей степени расхождения между F(x) и Fп(x) необходимо подсчитать взвешенную сумму квадратов разностей по всем разрядам статистического ряда
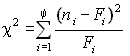 . . | (3.7) |
Величина c2 при неограниченном увеличении n имеет распределение хи-квадрат (асимптотически распределена как хи-квадрат). Это распределение зависит от числа степеней свободы k. Число степеней свободы равно числу y минус число линейных связей, наложенных на выборку. Одна связь существует в силу того, что любая частота может быть вычислена по совокупности частот в оставшихся y–1 разрядах. Кроме того, если параметры распределения неизвестны заранее, то имеется еще одно ограничение, обусловленное подгонкой распределения к выборке. Если по выборке определяются f параметров распределения, то число степеней свободы составит k=y–f–1.
Очевидно, что чем меньше расхождение между теоретическими и эмпирическими частотами, тем меньше величина критерия. Область принятия гипотезы Н0 определяется условием c2<c2(k; a), где c2(k; a) – критическая точка распределения хи-квадрат с уровнем значимости a. Вероятность ошибки первого рода равна a, вероятность ошибки второго рода четко определить нельзя, потому что существует бесконечно большое множество различных способов несовпадения распределений. Мощность критерия зависит от количества разрядов и объема выборки. Критерий рекомендуется применять при n>200, допускается применение при n>40, именно при таких условиях критерий состоятелен (как правило, отвергает неверную нулевую гипотезу).
Пример 1.Проверить с помощью критерия хи-квадрат гипотезу о нормальности распределения случайной величины, представленной статистическим рядом в табл. 2.4 при уровне значимости a=0,05.
Решение . В примере 2.3 были вычислены значения оценок моментов:
m1=27,51, m2=0,91, s=0,96.
На основе табл. 2.4 построим табл. 1, иллюстрирующую расчеты.
Таблица 1
| Номер интервала, i | ||||||
| ni | ||||||
| xi | 26,37 | 26,95 | 27,53 | 28,12 | 28,70 | бесконечность |
| F(xi) | 0,117 | 0,280 | 0,5 08 | 0,737 | 0,892 | |
| D Fi | 0,117 | 0,166 | 0,228 | 0,228 | 0,155 | 0,108 |
| Fi | 5,148 | 7,304 | 10,032 | 10,032 | 6,820 | 4,752 |
| (ni - Fi)2/Fi | 0,004 | 0,394 | 0,0001 | 0,1062 | 0,486 | 0,328 |
В этой таблице:
ni – частота попаданий элементов выборки в i-й интервал;
xi – верхняя граница i-го интервала;
F(xi) – значение функции нормального распределения;
DFi – теоретическое значение вероятности попадания случайной величины в i-й интервал
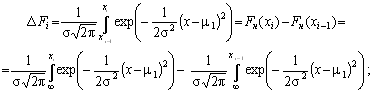
Fi=DFi*n – теоретическая частота попадания случайной величины в i-й интервал;
(ni–Fi)2/Fi – взвешенный квадрат отклонения.
Для нормального закона возможные значения случайной величины лежат в диапазоне от минус до плюс бесконечности, поэтому при расчетах оценок вероятностей крайний левый и крайний правый интервалы расширяются до минус и плюс бесконечности соответственно. Вычислить значения функции нормального распределения можно, воспользовавшись стандартными функциями табличного процессора или полиномом наилучшего приближения.
Сумма взвешенных квадратов отклонения c2=1,32. Число степеней свободы k = 6–1–2=3, так как уклонения связаны линейным соотношением
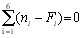 ,кроме того, на уклонения наложены еще две связи, ибо по выборке были определены два параметра распределения. Критическое значение c2(3; 0,05)=7,815 определяется по табл. П.3 приложения. Поскольку соблюдается условие c2<c2(3; 0,05), то полученный результат нельзя считать значимым и гипотеза о нормальном распределении генеральной совокупности не противоречит ЭД.
,кроме того, на уклонения наложены еще две связи, ибо по выборке были определены два параметра распределения. Критическое значение c2(3; 0,05)=7,815 определяется по табл. П.3 приложения. Поскольку соблюдается условие c2<c2(3; 0,05), то полученный результат нельзя считать значимым и гипотеза о нормальном распределении генеральной совокупности не противоречит ЭД.
Основная литература:
1. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 7-е, стер / Гмурман В.Е. – М.: Высш. шк., 1999. -479с.
2. Задачник по теории вероятностей и математической статистики. / Гмурман В.Е. – М., Высш. шк., 1999. -410с.
3. Теория вероятностей: Учеб. для вузов. – 7-е изд. стер. /Вентцель Е.С. – М.: Высш. шк., 2001. -575с.
Дополнительная литература:
1. Элементарная математика с точки зрения высшей: В 2 томах. /Ф. Клейн/ – М.: Наука, 1987
2. Высшая математика. Задачник /Бугров Я.С., Никольский С.М.- М.:Наука,2003.-432с.
3. Сборник задач по высшей математике /Минорский В.П.- М.:1971.-352с.
