Формулировка метода Гаусса для произвольной системы

Лекция 2

Метод Гаусса

§ 2. Метод Гаусса[1]

Простой пример применения метода

Освоение любой проблемы проще всего начать с разбора простого примера. Рассмотрим систему трех линейных уравнений:

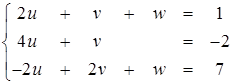(2.1)

Решение его по методу Гаусса или, как его еще называют, методу исключения состоит в последовательном исключении неизвестных.

1-й шаг: исключение u из 2-го и 3-го уравнений. Для этого, как нетрудно убедиться, можно вычесть из второго уравнения первое, умноженное на 2, а третье уравнение сложить с первым:

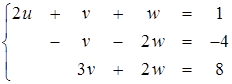(2.2)

2-й шаг: исключение v из 3-го уравнения. Для этого второе уравнение умножаем на 3 и складываем с последним, третьим:

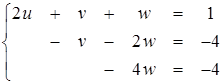(2.3)

3-й шаг: решение треугольной системы. Треугольный вид (2.3), к которому приведена система (2.1), позволяет легко определить неизвестные, двигаясь от нижней строки системы к верхней:

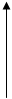
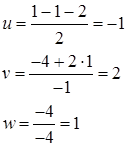(2.4)

Формулировка метода Гаусса для произвольной системы

Таким образом, метод Гаусса для системы линейных уравнений порядка n:

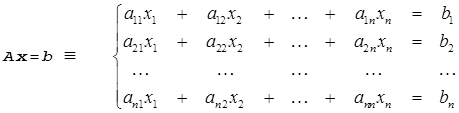(2.5)

можно описать следующим образом:

1. Первое уравнение системы остается без изменений, а из остальных исключается первое неизвестное 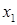. Это достигается вычитанием из второго уравнения первого уравнения, умноженного на 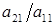; из третьего уравнения - первого уравнения, умноженного на 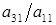; ... ; из n-го уравнения ‑ первого уравнения, умноженного на 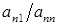. В результате этого исключения система (2.5) приводится к виду

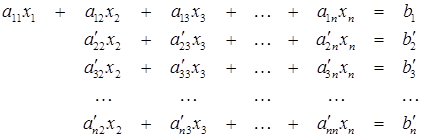(2.6)

Отметим, что последние (n-1) уравнений образуют систему (n-1) уравнений с (n-1) неизвестными 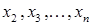. Штрих при коэффициентах и т.д. напоминает нам о том, что эти величины отличаются от исходных 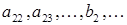из (2.5). Конечно, мы могли бы в системе (2.6) указать точные значения этих величин, например, 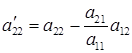. Однако это сделало бы нашу простую схему загроможденной буквами и знаками операций и, поэтому, малопонятной.

2. Далее поступаем с нижними (n-1) строками системы (2.6) так же, как поступили со всей системой на первом этапе. В результате (2.6) приводится к виду

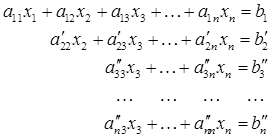(2.7)

Здесь два штриха в 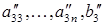и т.д. напоминают о том, что эти величины получены после исключения второй неизвестной. И в дальнейшем новое значение коэффициента 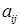или 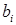, полученное после исключения k-й неизвестной, будем обозначать 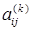или 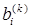. Продолжаем процесс исключения для 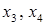и т.д. до тех пор, пока не будет исключено 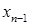из n-го уравнения. В результате исходная система будет приведена к треугольному виду:

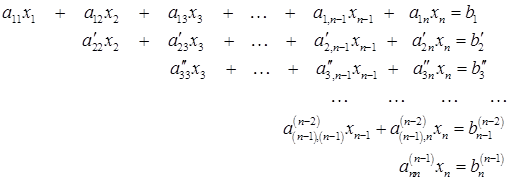(2.8)

3. Обратный ход. Из последнего уравнения (2.8), в котором лишь одна неизвестная, легко определяем 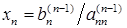. В предпоследнем уравнении две неизвестных, одну из которых мы уже успели определить. Поднимаясь, таким образом, со строки на строку системы (2.8), мы очень просто определяем одну за другой неизвестные .

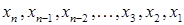Здесь наступил подходящий момент ввести понятие ведущего элемента. Ведущим элементом системы линейных уравнений 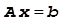или матрицы A называются первые ненулевые коэффициенты системы, полученные после гауссова исключения. В (2.8) такими ведущими элементами являются .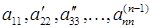