Многоцелевая оптимизация. Оптимизация по Парето
Каждый предмет и каждое явление имеют бесконечное число сторон и поэтому полностью могут быть описаны лишь бесконечным числом уравнений с бесконечным числом членов. Таким образом, любое реальное математическое описание предмета или явления носит частичный, приближенный характер, охватывающий лишь некоторые стороны предмета или исследованного явления, при этом не всегда существенные для поставленной цели исследования. Отсюда следует, что представления о любом предмете или любом явлении могут и должны непрерывно уточняться, соответственно могут и должны уточняться и математические зависимости, описывающие эти модели. Число таких приближений и уточнений бесконечно.
При наличии многих, да еще и противоречивых целей, а также различных типов исходной информации системе, естественно, появляются различные альтернативы решения. Термин «альтернатива» имеет ряд синонимов, в зависимости от конкретных особенностей задачи. В частности, употребляются следующие термины: вариант, план, траектория движения системы и др. Среди возможных альтернатив желательно выбрать наилучшую в определенном смысле, или как принято говорить, найти оптимальное решение задачи. При этом даже без особого анализа ясно, что если различные цели противоречивы и не взаимозаменяемы, то их «примирение», отыскание какого-то компромисса очень непростая задача. Кроме того, к противоречивости целей следует добавить еще одно крайне неприятное свойство большой системы – отсутствие достаточно полных сведений как о ней самой, так и о ее взаимодействии с окружающей средой.
Оптимизация по Парето.
В настоящее время понятие множества оптимальных по Парето решений относится к числу основополагающих в общей теории принятия решений. Это множество используется в случаях, когда в многокритериальных задачах разные критерии несопоставимы, или, как обычно говорят, для них отсутствуют какие-либо предпочтения. Это означает, что улучшение решения по одному какому-либо критерию допустимо и оправдано лишь в случае, когда наряду с этим не происходит ухудшения решения хотя бы по одному другому критерию. Под множеством Парето-оптимальных решений понимают такое, когда ни одно из решений этого множества не может быть заменено другим, более хорошим по какому-либо критерию без того, чтобы не ухудшить решение хотя бы по одному другому критерию. Следовательно, каждое решение, принадлежащее множеству Парето, лучше других из этого же множества по каким-то одним и хуже по другим критериям. Так как критерии несопоставимы, то среди этих решений нет ни одного, которое было бы лучше других во всех отношениях. Что же касается решений, не принадлежащих множеству Парето, то все они хуже, по крайней мере, по одному критерию. Именно поэтому множество Парето называют эффективным, и дальнейший поиск с привлечением каких-либо дополнительных условий или процедур естественно выполняется только на множестве Парето.
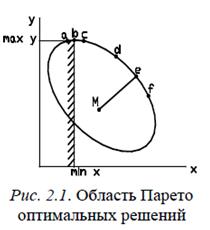
Поясним сказанное с помощью простейшей задачи, когда имеются два несопоставимых критерия х и y, и оптимизация означает максимизацию обоих критериев (принципиальная сторона вопроса сохраняется и при минимизации).
Пусть все множество допустимых решений образует представленную на рис. 2.1 область, ограниченную осями x и y в положительном квадранте и кривой abcdef (включая и точки, лежащие на этой кривой). При этом будем помнить, что метрики (единицы измерения) критериев x и y несопоставимы. Примем в качестве начальной некоторую альтернативу – точку M с значениями критериев xM и yM. Очевидно, что переход из точки M в одну из точек кривой, ограниченной точками с и f, означает улучшение решения хотя бы по одному критерию без ухудшения по другому. Все промежуточные точки на кривой cf лучше точек внутри области по обоим критериям совместно. Однако переход из точки c в точку f или наоборот невозможен без ухудшения одного из критериев. Все решения, соответствующие точкам на кривой cf, принадлежат множеству Парето-оптимальных решений. При этом каждому решению, соответствующему любой другой точке допустимой области, всегда можно противопоставить не менее одного решения из множества Парето, которое лучше по крайней мере по одному и не хуже по другому критерию. Для случаев нескольких критериев принципиальная картина сохраняется, разумеется, для многомерного пространства критериев.