Требования, предъявляемые к моделям

Для того, чтобы создаваемая модель соответствовала своему назначению, недостаточно создать просто модель. Необходимо, чтобы она отвечала ряду требований, обеспечивающих ее функционирование. Невыполнение этих требований лишает модель ее модельных свойств.

Первым таким требованием является ее ингерентность, то есть достаточная степень согласованности создаваемой модели со средой, чтобы создаваемая модель была согласована с научной средой, в которой ей предстоит функционировать.

Другой аспект ингерентности модели состоит в том, что в ней должны быть предусмотрены не только «стыковочные узлы» со средой (интерфейсы), но, и, что не менее важно, в самой среде должны быть созданы предпосылки, обеспечивающие функционирование создаваемой модели. То есть не только модель должна приспосабливаться к среде, но и среду необходимо приспосабливать к модели будущей системы.

Второе требование – простота модели. С одной стороны, простота модели – ее неизбежное свойство: в модели невозможно зафиксировать все многообразие реальной ситуации. С другой стороны, простота модели неизбежна из-за необходимости оперирования с ней, использования ее как рабочего инструмента, который должен быть обозрим и понятен. С третьей стороны, есть еще один, довольно интересный и непонятный пока аспект требования простоты модели, который заключается в том, что чем проще модель, тем она ближе к моделируемой реальности и тем она удобнее для использования. Классический пример – геоцентрическая модель Птолемея и гелиоцентрическая модель Коперника.

Обе модели позволяют с достаточной точностью вычислять движение планет, предсказывать затмения Солнца и т.п. Но модель Коперника истинна и намного проще для использования, чем модель Птолемея. Ведь недаром еще древние подметили, что простота – печать истины. У физиков, математиков, к примеру, есть довольно интересный критерий оценки решения теоретических задач: если решение простое и «красивое» – то, скорее всего, и истинное.

Наконец, третье требование, предъявляемое к модели – ее адекватность. Адекватность модели означает, что она достаточно полна, точна и истинна. Достаточно не вообще, а именно в той мере, которая позволяет достичь поставленной цели.

Иногда удается (и это желательно) ввести некоторую меру адекватности модели, то есть определить способ сравнения разных моделей по степени успешности достижения цели с их помощью.

Таким образом, мы выделили три основных требования, предъявляемых к моделям: ингерентности, простоты и адекватности как отношения моделей с тремя остальными «участниками» процесса моделирования: со средой (ингерентность), с субъектом, создающим и/или использующим модель (простота), с моделируемым объектом, то есть с создаваемой системой (адекватность).

Методы моделирования.

Методы моделирования систем можно разделить на два класса. Называются эти классы в разных публикациях по-разному:

– методы качественные и количественные. Смысл разделения понятен. Однако такое разделение не совсем точно, поскольку качественные методы могут сопровождаться при обработке получаемых результатов и количественными представлениями, например с использованием средств математической статистики;

– методы, использующие средства естественного языка, и методы, использующие специальные языки. Смысл разделения также понятен, но тоже не совсем точен, поскольку графические методы (схемы, диаграммы и т.д.) в первый класс не попадают, но широко используются в науке;

– методы содержательные и формальные. Тоже не точно, поскольку компьютерное моделирование может требовать минимальной формализации.

И так далее.

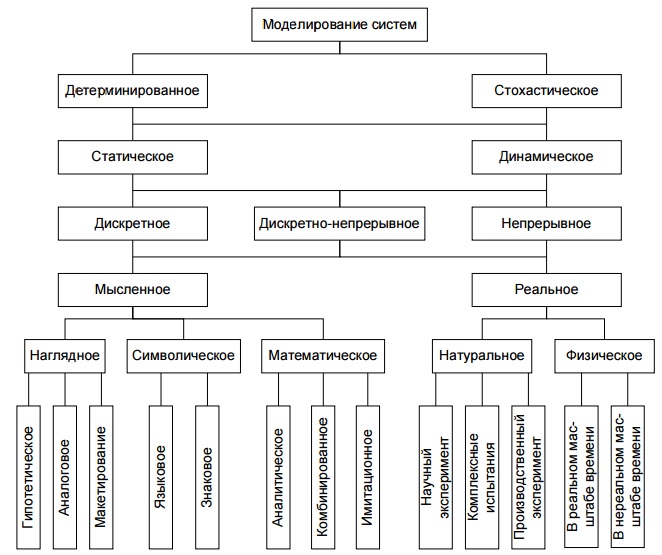
Существует множество более детальных классификаций моделей и/или видов моделирования. Ниже приведена система классификаций видов моделирования, заимствованная из общедоступной литературы.

Качественные методы моделирования. Рассмотрим некоторые качественные методы моделирования. Наиболее распространенным «качественным» методом моделирования, применяемым, в том числе, в рамках комплексного прогнозирования, является метод сценариев.

Метод «сценариев». Метод подготовки и согласования представлений о проектируемой системе, изложенных в письменном виде, получил название метода «сценариев».

Первоначально этот метод предполагал подготовку текста, содержащего логическую последовательность событий или возможные варианты решения той или иной проблемы, развернутые во времени. Однако позднее обязательное требование временных координат было снято, и сценарием стал называться любой документ, содержащий анализ рассматриваемой проблемы и предложения по ее решению, по развитию системы, независимо от того, в какой форме он представлен.

Как правило, предложения для подготовки подобных документов пишутся экспертами вначале индивидуально, а затем формируется согласованный текст.

Сценарий требует не только содержательных рассуждений, помогающих не упустить детали, но и содержит, как правило, результаты количественного технико-экономического и/или статистического анализа с предварительными выводами. Группа экспертов, подготавливающая сценарий, пользуется обычно правом получения необходимых сведений от тех или иных организаций, необходимых консультаций.

Роль специалистов при подготовке сценария – выявить общие закономерности развития системы; проанализировать внешние и внутренние факторы, влияющие на ее развитие и формулирование целей; провести анализ высказываний ведущих специалистов в периодической печати, научных публикациях и других источниках информации; создать вспомогательные информационные фонды, способствующие решению соответствующей проблемы.

В последнее время понятие сценария расширяется в направлении как областей применения, так и форм представления и методов их разработки: в сценарий вводятся количественные параметры и устанавливаются их взаимозависимости, предлагаются методики подготовки сценария с использованием компьютеров.

Сценарий позволяет создать предварительное представление о системе. Однако сценарий – это все же текст со всеми вытекающими последствиями (синонимия, омонимия, парадоксы), обусловливающими возможность неоднозначного его толкования. Вспомним Ф. Тютчева: «Мысль изреченная есть ложь». Поэтому его следует рассматривать как основу для дальнейшей разработки модели.

Графические методы. Графические представления позволяют наглядно отработать структуру моделируемых систем и процессов, происходящих в них. В этих целях используются графики, схемы, диаграммы, гистограммы, древовидные структуры и т.д. Дальнейшим развитием графических методов стало использование, в частности, теории графов и возникших на ее основе методов календарно-сетевого планирования и управления.

Метод структуризации. Структурные представления разного рода позволяют разделить сложную проблему с большой неопределенностью на более мелкие, лучше поддающиеся анализу, что само по себе можно рассматривать как некоторый метод моделирования, именуемый иногда системно-структурным. Виды структур, получаемые путем расчленения системы во времени – сетевые структуры или в «пространстве» – иерархические структуры, матричные структуры.

Количественные методы моделирования (математическое моделирование). Для исследования того или иного объекта математическими методами, включая и компьютерное моделирование, должна быть проведена формализация этого процесса, то есть построена математическая модель.

Методы математического моделирования можно в равной степени рассматривать и как методы научного исследования.

Под математическим моделированием понимается процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта и требуемой достоверности и точности решения этих задач.

Любая математическая модель, как и всякая другая, описывает реальный объект лишь с некоторой степенью приближения к действительности.

Можно выделить следующие этапы построения математической модели (см. также Рис. 13 и детализацию этапов ниже).

1. Определение предмета и цели моделирования, включая границы исследуемого объекта и те основные свойства, которые должны быть отражены моделью.

2. Выбор языка (аппарата) моделирования. На сегодняшний день не существует общепризнанной классификации методов математического моделирования. Существуют несколько десятков «аппаратов» моделирования, каждый из которых представляет собой разветвленный раздел математики. Описывать всех их подробно в рамках настоящей книги не представляется возможным (да и целесообразным).

3. Выбор переменных, описывающих состояние системы и существенные параметры внешней среды, а также шкал их измерения и критериев оценки (см. также Рис. 13).

4. Выбор ограничений, то есть множеств возможных значений переменных, и начальных условий (начальных значений переменных).

5. Определение связей между переменными с учетом всей имеющейся о моделируемом объекте информации, а также известных законов, закономерностей и т.п., описывающих его.

6. Исследование модели – или имитационное, или/и применение методов оптимизации.

7. Изучение устойчивости и адекватности модели.

Последующие этапы, связанные с практической реализацией модели и/или внедрением результатов моделирования, мы здесь не рассматриваем.

Приведенные этапы математического моделирования иногда приходится повторять, возвращаясь к более ранним этапам при уточнении цели моделирования, обеспечении точности, устойчивости, адекватности и т.д.

Завершив описание общих этапов математического моделирования, отметим, что последнее можно разделить на аналитическое и имитационное.

Для аналитического моделирования характерно то, что процессы функционирования элементов объекта записываются в виде некоторых функциональных соотношений (например, уравнений – алгебраических, дифференциальных, интегральных и т.п.) или логических условий. Аналитическая модель может быть исследована следующими методами:

- аналитическим, когда стремятся получить в общем (аналитическом) виде явные зависимости для искомых характеристик в виде определенных формул;

- численным, когда, не имея возможности решать уравнения в общем виде, стремятся получить числовые результаты при тех или иных конкретных начальных данных (например, с помощью компьютера);

- качественным, когда, не имея решения в явном виде, можно найти некоторые его свойства. Примером могут служить так называемые «мягкие» модели, в которых, например, анализ вида дифференциальных уравнений, описывающих самые разнообразные процессы (экономические, экологические, политические и др.) позволяет делать качественные выводы о свойствах их решений – существовании и типе равновесных точек, областях возможных значений переменных и т.п.

Для имитационного моделирования характерно исследование отдельных траекторий динамики моделируемого объекта. При этом фиксируются некоторые начальные условия (начальное состояние объекта или параметры модели) и рассчитывается одна траектория. Затем выбираются другие начальные условия, и рассчитывается другая траектория и т.д. То есть, аналитической зависимости между параметрами модели и будущими состояниями системы не ищется. Как правило, при имитационном моделировании используют численные методы, реализованные на компьютере. Плюс имитационного моделирования заключается в том, что оно позволяет проанализировать различные сценарии иногда даже для очень сложных моделей. Его недостаток состоит в отсутствии возможности получения, например, ответа на вопрос, в каких случаях (при каких значениях начальных условий и параметров модели) динамика системы будет удовлетворять заданным требованиям. Кроме того, обычно затруднителен анализ устойчивости имитационных моделей.

Итак, мы кратко рассмотрели вопрос о построении моделей, в том числе – математических (обсуждение устойчивости и адекватности моделей, а также связанных с моделями проблем оптимизации и задач управления, производится ниже).

С современными способами формализованного представления моделей можно ознакомиться в соответствующей специализированной литературе.

Отметим, что, несмотря на то, что на сегодняшний день накоплен значительный опыт разработки и использования самых разных методов моделирования (в том числе – математического), все равно в этом процессе решающую роль играет творчество, интуитивное искусство создания модели.

Оптимизация

Оптимизация в широком смысле слова находит применение в науке, технике и в любой другой области человеческой деятельности.

Оптимизация - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.

Поиски оптимальных решений привели к созданию специальных математических методов и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и др). Однако до второй половины 20 века методы оптимизации во многих областях науки и техники применялись очень редко, поскольку практическое использование математических методов оптимизации требовало огромной вычислительной работы, которую без ЭВМ реализовать было крайне трудно, а в ряде случаев - невозможно. При наличии ЭВМ задача заметно упрощается.

В процессе проектирования ставится обычно задача определения наилучших, в некотором смысле, структуры или значений параметров объектов. Такая задача называется оптимизационной. Если оптимизация связана с расчётом оптимальных значений параметров при заданной структуре объекта, то она называется параметрической оптимизацией. Задача выбора оптимальной структуры является структурной оптимизацией.