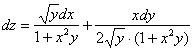Особенности вычисления частных производных

Подведем итог, чем же отличается нахождение частных производных от нахождения «обычных» производных функции одной переменной:

1) Когда мы находим частную производную 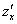, то переменная 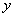считается константой.

2) Когда мы находим частную производную 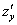, то переменная 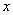считается константой.

3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (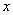 , 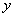либо какой-нибудь другой), по которой ведется дифференцирование.

Шаг второй. Находим частные производные второго порядка. Их четыре.

Обозначения:

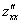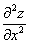или – вторая производная по «икс»

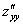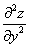или – вторая производная по «игрек»

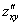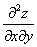или – смешанная производная «по икс игрек»

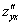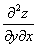или – смешанная производная «по игрек икс»

В понятии второй производной нет ничего сложного. Говоря простым языком, вторая производная – это производная от первой производной.

Для наглядности я перепишу уже найденные частные производные первого порядка:

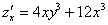
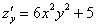
Сначала найдем смешанные производные:

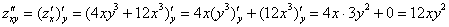
Как видите, всё просто: берем частную производную 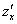и дифференцируем ее еще раз, но в данном случае – уже по «игрек».

Аналогично:

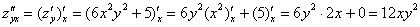
Для практических примеров, когда все частные производные непрерывны, справедливо следующее равенство:

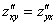
Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.

Находим вторую производную по «икс».

Никаких изобретений, берем 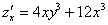и дифференцируем её по «икс» еще раз:

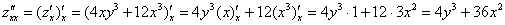
Аналогично:

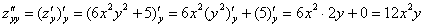
Следует отметить, что при нахождении 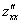, 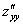нужно проявить повышенное внимание, так как никаких чудесных равенств для проверки не существует.

Пример 2

Найти частные производные первого и второго порядка функции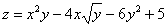

Это пример для самостоятельного решения (ответ в конце урока).

При определенном опыте частные производные из примеров №№1,2 будут решаться Вами устно.

Переходим к более сложным примерам.

Пример 3

Найти частные производные первого порядка функции 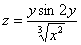. Проверить, что 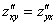. Записать полный дифференциал первого порядка .

Решение: Находим частные производные первого порядка:

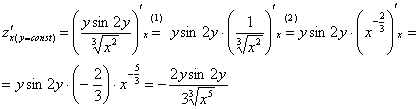
Обратите внимание на подстрочный индекс: , рядом с «иксом» не возбраняется в скобках записывать, что 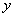– константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.

Дальнейшие комментарии:

(1) Выносим все константы за знак производной. В данном случае 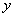и 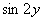, а, значит, и их произведение 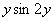считается постоянным числом.

(2) Не забываем, как правильно дифференцировать корни.

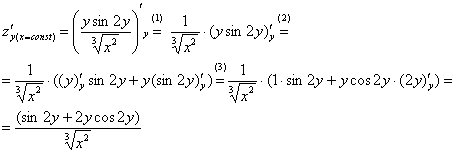
(1) Выносим все константы за знак производной, в данной случае константой является .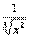

(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения .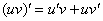

(3) Не забываем, что 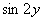– это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .

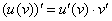Теперь находим смешанные производные второго порядка:

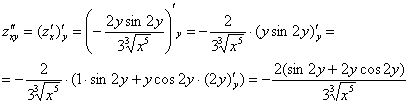
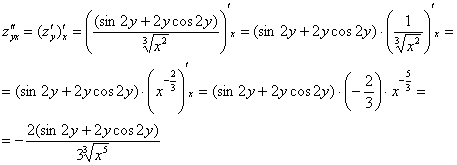
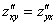, значит, все вычисления выполнены верно.

Запишем полный дифференциал 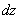. В контексте рассматриваемого задания не имеет смысла рассказывать, что такое полный дифференциал функции двух переменных. Важно, что этот самый дифференциал очень часто требуется записать в практических задачах.

Полный дифференциал первого порядка функции двух переменных имеет вид:

.

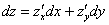В данном случае:

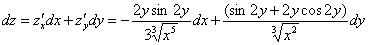
То есть, в формулу нужно просто подставить уже найденные частные производные первого порядка. Значки дифференциалов 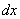и 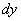в этой и похожих ситуациях по возможности лучше записывать в числителях:

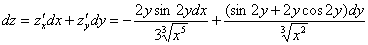
Пример 4

Найти частные производные первого порядка функции 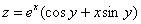. Проверить, что 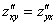. Записать полный дифференциал первого порядка .

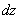Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.

Рассмотрим серию примеров, включающих в себя сложные функции.

Пример 5

Найти частные производные первого порядка функции .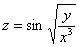

Записать полный дифференциал .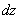

Решение:

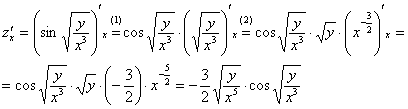
(1) Применяем правило дифференцирования сложной функции 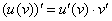. С урока Производная сложной функцииследует помнить очень важный момент: когда мы по таблице превращаем синус (внешнюю функцию) в косинус, то вложение 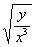(внутренняя функция) у нас не меняется.

(2) Здесь используем свойство корней: 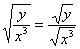, выносим константу 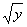за знак производной, а корень 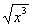представляем в нужном для дифференцирования виде.

Аналогично: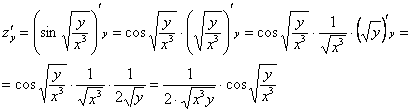

Запишем полный дифференциал первого порядка: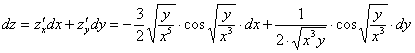

Пример 6

Найти частные производные первого порядка функции .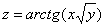

Записать полный дифференциал .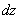

Это пример для самостоятельного решения (ответ в конце урока). Полное решение не привожу, так как оно достаточно простое

Довольно часто все вышерассмотренные правила применяются в комбинации.

Пример 7

Найти частные производные первого порядка функции .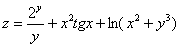

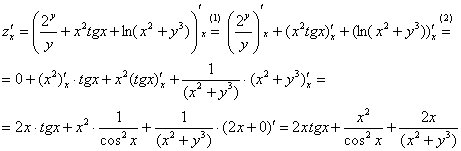
(1) Используем правило дифференцирования суммы.

(2) Первое слагаемое в данном случае считается константой, поскольку в выражении 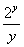нет ничего, зависящего от «икс» – только «игреки».

(Знаете, всегда приятно, когда дробь удается превратить в ноль).

Для второго слагаемого применяем правило дифференцирования произведения. Кстати, в алгоритме ничего бы не изменилось, если бы вместо 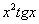была дана функция 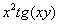– важно, что здесь мы имеем произведение двух функций, КАЖДАЯ из которых зависит от «икс», поэтому нужно использовать правило дифференцирования произведения. Для третьего слагаемого применяем правило дифференцирования сложной функции.

Найдем теперь частную производную по y:

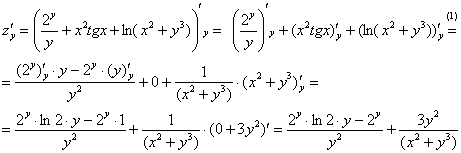
(1) В первом слагаемом и в числителе и в знаменателе содержится «игрек», следовательно, нужно использовать правило дифференцирования частного: 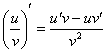. Второе слагаемое зависит ТОЛЬКО от «икс», значит, 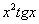считается константой и превращается в ноль. Для третьего слагаемого используем правило дифференцирования сложной функции.

Для тех читателей, которые мужественно добрались почти до конца урока, расскажу старый мехматовский анекдот для разрядки.

Однажды в пространстве функций появилась злобная производная и как пошла всех дифференцировать. Все функции разбегаются кто куда, никому не хочется превращаться! И только одна функция никуда не убегает. Подходит к ней производная и спрашивает:

– А почему это ты от меня никуда не убегаешь?

– Ха. А мне всё равно, ведь я «е в степени икс», и ты со мной ничего не сделаешь!

На что злобная производная с коварной улыбкой отвечает:

– Вот здесь ты ошибаешься, я тебя продифференцирую по «игрек», так что быть тебе нулем.

(Кто понял анекдот, тот освоил производные, минимум, на «тройку»).

Пример 8

Найти частные производные первого порядка функции .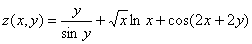

Это пример для самостоятельного решения. Полное решение и образец оформления задачи – в конце урока.

Пример 9

Дана функция двух переменных 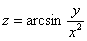. Найти все частные производные первого и второго порядков.

Это пример для самостоятельного решения. Полное решение и образец оформления где-то рядом.

Решения и ответы:

Пример 2:

, , ,

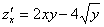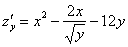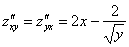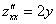
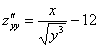
Пример 4: Ссылка для просмотра ниже.

Пример 6:

, ,
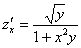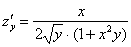