Бесконечно малые последовательности
Последовательность аn называется бесконечно малой , это означает, что предел этой последовательности после равен 0.
an – бесконечно малая Û lim an=0 то есть для любого ε>0 существует N, такое что для любого n>N выполняется n®+¥ |an|<ε
Важные примеры бесконечно малой последовательности:
1)an=1/n Докажем, что для любого ε>0 |1/n|<ε Þ 1/n<εÞ n>1/εÞ N[1/ε]+1
Свойства бесконечно малой последовательности.
Теорема. Сумма бесконечно малой есть бесконечно малое.
anbn®бесконечно малое Þ an+bn – бесконечно малое.
Теорема Произведение бесконечно малого есть бесконечно малое.
an,bn – бесконечно малое Þ anbn – бесконечно малое.
Теорема Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность
аn – ограниченная последовательность
an –бесконечно малая последовательность Þ anan – бесконечно малая последовательность.
Теорема о представление последовательности имеющий конечный предел.
lim an=a Û an=a+an
n®+¥
Последовательность an имеет конечный предел а тогда и только тогда, когда она представлена в виде an=a+an
где an – бесконечно малая.
Вещественные числаэто все числа, которые можно расположить на числовой прямой. В любом случае, их бесконечно много, ими могут быть любые дроби, целые и натуральные числа, т.к. вещественные числа это надмножество всех остальных (кроме комплексных). Теорема о вложенных отрезкахДля всякой системы вложенных отрезков существует хотя бы одна точка, принадлежащая всем отрезкам данной системы. Рассмотрим множество 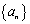 левых концов наших отрезков лежит на числовой прямой левее множества правых концов отрезков
левых концов наших отрезков лежит на числовой прямой левее множества правых концов отрезков 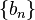 , поскольку Очевидно, что 1)
, поскольку Очевидно, что 1) 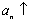 2)
2) 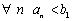 В силу аксиомы непрерывности, существует точка С, разделяющая эти два множества, то есть
В силу аксиомы непрерывности, существует точка С, разделяющая эти два множества, то есть 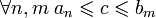 в частности
в частности 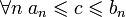 Последнее неравенство означает, что С — общая точка всех отрезков данной системы. 2. Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки с и с|, принадлежащие всем отрезкам системы:
Последнее неравенство означает, что С — общая точка всех отрезков данной системы. 2. Единственность общей точки. Пусть длина отрезков системы стремится к нулю. Покажем, что существует только одна точка, принадлежащая всем отрезкам системы. Предположим противное: пусть имеется две различные точки с и с|, принадлежащие всем отрезкам системы: 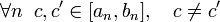 Тогда для всех номеров n выполняются неравенства:
Тогда для всех номеров n выполняются неравенства: 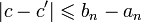 В силу условия стремления к нулю длин отрезков для любого
В силу условия стремления к нулю длин отрезков для любого 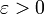 для всех номеров n, начиная с некоторого будет выполняться неравенство
для всех номеров n, начиная с некоторого будет выполняться неравенство 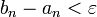 Взяв в этом неравенстве
Взяв в этом неравенстве 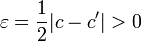 , получим
, получим 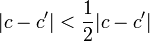 Противоречие. Лемма доказана полностью.
Противоречие. Лемма доказана полностью.
Предел последовательности. Предел последовательности числа а , называется пределом числовой последовательности аn, если для любого сколь угодно малого числа ε>0, найдётся натуральный номер N такой, что для всех чисел n³N выполняется модуль разности 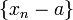
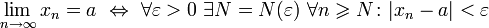
Примеры: Доказать, что ln(-1)2/n=0
Зададим любое ε>0, хотим чтобы |(-1)n-0|<ε, начиная с некоторого номера N, 1/n<ε Þ n>1/ε
N=[1/ε]+1
ε=0.01
N=[1/0.01]+1=101
|an|<0.01, если n³101
* * *
an=1-1/n2
lim(1-1/n2)=1
n®+¥
Для любого ε>0 |(1-1/n2)-1|<ε
|-1/n2|<ε Þ 1/n2<ε Þ n2>1/ε Þ n>1/Öε
N=[1/Öε]+1
Теорема о единственности предела. Если 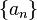 - сходящаяся, то предел единственный.
- сходящаяся, то предел единственный.
Доказательство. Пусть 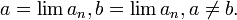 для определённости
для определённости 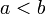 имеем:
имеем:
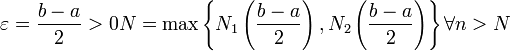
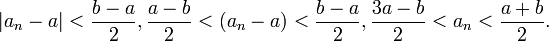
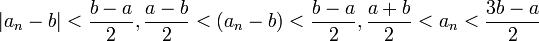 .
.
Получили противоречие 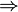 предел единственный.
предел единственный.
Теорема. Сходящиеся последовательности ограничены.
Доказательство. Пусть 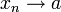 при
при 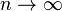
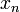

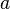
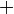
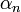 ,
, 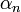 - бесконечно малая последовательность.
- бесконечно малая последовательность.
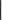
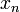
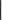

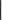
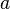
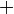
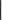
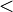
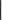
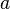
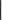
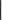
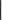
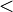
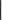
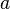
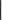
 , где
, где 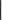
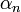
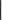
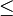
 ,
, 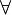
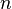
5) Теорема о сжатой переменной
Формулировка: Если существуют 3 последовательности, элементы одной из которых начиная с некоторого номера будут между элементами двух других при равных номерах, а также 2 другие последовательности имеют конечные пределы, и эти пределы равны, то наша последовательность тоже будет сходится к конечному пределу, и этот предел будет равен пределам двух других последовательностей.
Доказательство:
аn<bn<cn начиная с некоторого N
предел аn равен d и предел cn равен d
(!) что у последовательности bn тоже есть предел и он равен d
рассмотрим E>0
предел аn равен d, следовательно существует номер N1, начиная с которого |аn-d|<E, то есть E-d<аn<E+d
предел cn равен d, следовательно существует номер N2, начиная с которого |аn-d|<E, то есть E-d<cn<E+d
выберем наибольший из номеров (N)
тогда:
E-d<аn<bn<cn<E+d
то есть E-d<bn<E+d, следовательно последовательность bn имеет конечный предел и он равен d (если последнее не понятно из предыдущей записи, то просто смотрим на теорему №4: предел bn не меньше и не больше d, следовательно равен)
что и требовалась доказать.
