ДЕ9. Математическая статистика
1)Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 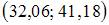 для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна … 36,62
для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна … 36,62
Решение:
Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки. Тогда точечная оценка будет равна 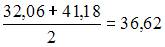
Тема: Проверка статистических гипотез
Соотношением вида 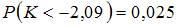 можно определить …
можно определить …
 | левостороннюю критическую область |
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии 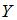 на
на 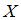 имеет вид
имеет вид 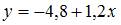 .
.
Тогда выборочный коэффициент корреляции может быть равен …
 | 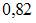 |
Решение:
Значение выборочного коэффициента корреляции, во-первых, принадлежит промежутку 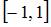 а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение
а во-вторых, его знак совпадает со знаком выборочного коэффициента регрессии. Этим условиям удовлетворяет значение 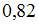
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 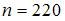
гистограмма частот которой имеет вид:
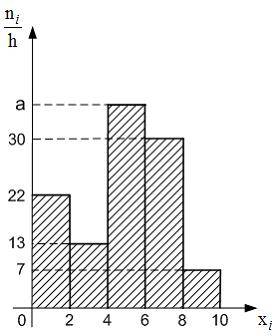
Тогда значение a равно …
 |
Решение:
Так как объем выборки вычисляется как 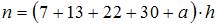 где
где 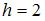 то
то
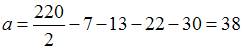
Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
 | 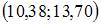 | ||
Тема: Проверка статистических гипотез
Основная гипотеза имеет вид 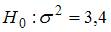 . Тогда конкурирующей может являться гипотеза …
. Тогда конкурирующей может являться гипотеза … 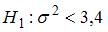
Решение:
Конкурирующей (альтернативной) называют гипотезу, которая противоречит основной гипотезе. Условию 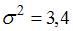 противоречит
противоречит 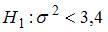 .
.
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 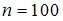 , полигон частот которой имеет вид:
, полигон частот которой имеет вид:
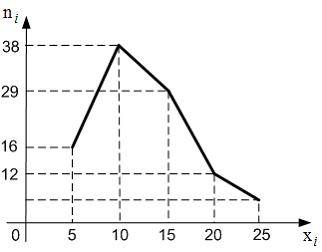
Тогда относительная частота варианты 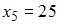 в выборке равна …
в выборке равна …  0,05
0,05
Решение:
Относительная частота 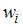 вычисляется по формуле
вычисляется по формуле 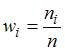 , где
, где 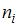 – частота варианты
– частота варианты 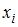 , а
, а 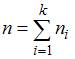 – объем выборки. Вычислим предварительно частоту варианты
– объем выборки. Вычислим предварительно частоту варианты 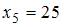 как
как 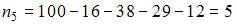 . Тогда
. Тогда 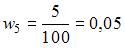
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 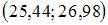 для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …
для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …
 | 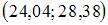 |
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала 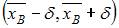 , где точечная оценка математического ожидания
, где точечная оценка математического ожидания 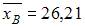 , а точность оценки
, а точность оценки 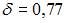 . В случае увеличения надежности точность оценки ухудшается, то есть значение
. В случае увеличения надежности точность оценки ухудшается, то есть значение 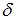 будет больше 0,77.
будет больше 0,77.
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 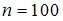

Тогда относительная частота варианты  равна …
равна …
 | 0,25 |
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии 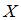 на
на 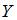 имеет вид
имеет вид 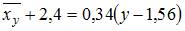 . Тогда выборочное среднее признака
. Тогда выборочное среднее признака 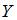 равно …
равно … 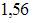
Тема: Проверка статистических гипотез
Левосторонняя критическая область может определяться из соотношения … 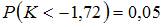
Решение:
Левосторонней называют критическую область, определяемую соотношением 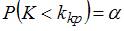 , где
, где 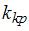 – отрицательное число, а
– отрицательное число, а 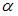 – уровень значимости. Таким соотношением является
– уровень значимости. Таким соотношением является 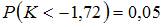
Тема: Проверка статистических гипотез
Двусторонняя критическая область может определяться из соотношения …
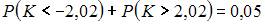
Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид …
 | 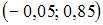 |
Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
 | 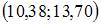 | ||
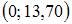 | |||
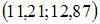 | |||
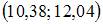 |
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала 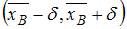 , где точечная оценка математического ожидания
, где точечная оценка математического ожидания 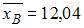 , а точность оценки
, а точность оценки 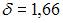 .
.
Следовательно, интервальная оценка будет иметь вид 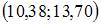
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 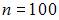 , гистограмма относительных частот которой имеет вид
, гистограмма относительных частот которой имеет вид
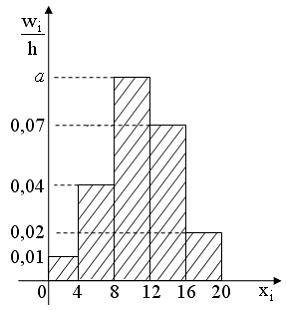
Тогда значение a равно …
Тема: Проверка статистических гипотез
Соотношением вида 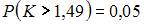 можно определить …
можно определить …
 | правостороннюю критическую область | ||
| левостороннюю критическую область | |||
| двустороннюю критическую область | |||
| область принятия гипотезы |
Решение:
Данное соотношение определяет правостороннюю критическую область, так как правосторонней называют критическую область, определяемую соотношением вида 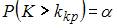 , где
, где 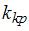 – положительное число, а
– положительное число, а 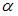 – уровень значимости.
– уровень значимости.
Тема: Проверка статистических гипотез
Левосторонняя критическая область может определяться из соотношения …
 | 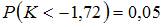 | ||
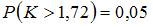 | |||
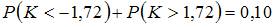 | |||
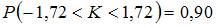 |
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии 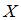 на
на 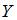 имеет вид
имеет вид 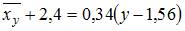 . Тогда выборочное среднее признака
. Тогда выборочное среднее признака 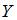 равно …
равно …
 | 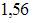 | ||
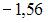 | |||
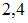 | |||
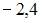 |
Решение:
Выборочное уравнение прямой линии регрессии 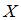 на
на 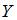 имеет вид
имеет вид 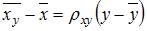 . Тогда выборочное среднее признака
. Тогда выборочное среднее признака 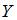 равно
равно 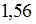 .
.
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 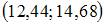 для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …
 | 1,12 | ||
| 0,01 | |||
| 2,24 | |||
| 13,56 |
Тема: Статистическое распределение выборки
Статистическое распределение выборки имеет вид

Тогда значение относительной частоты 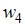 равно …
равно …
 | 0,25 | ||
| 0,05 | |||
| 0,26 | |||
| 0,75 |
Решение:
Сумма относительных частот равна единице. Поэтому 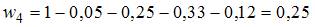 .
.
Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Решение задачи Коши 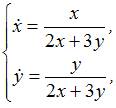
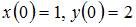 , имеет вид …
, имеет вид … 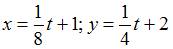
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии 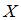 на
на 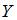 имеет вид
имеет вид 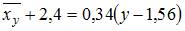 . Тогда выборочное среднее признака
. Тогда выборочное среднее признака 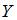 равно …
равно …
 | 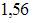 | ||
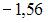 | |||
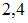 | |||
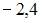 |
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 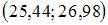 для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …
для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …
 | 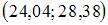 | ||
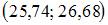 | |||
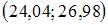 | |||
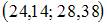 |
Решение:
Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала 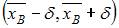 , где точечная оценка математического ожидания
, где точечная оценка математического ожидания 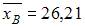 , а точность оценки
, а точность оценки 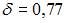 . В случае увеличения надежности точность оценки ухудшается, то есть значение
. В случае увеличения надежности точность оценки ухудшается, то есть значение 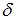 будет больше 0,77.
будет больше 0,77.
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 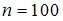 :
:

Тогда относительная частота варианты  равна …
равна …
 | 0,25 | ||
| 0,75 | |||
| 0,24 | |||
| 0,04 |
Тема: Проверка статистических гипотез
Соотношением вида 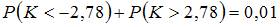 можно определить …
можно определить …
 | двустороннюю критическую область | ||
| правостороннюю критическую область | |||
| левостороннюю критическую область | |||
| область принятия гипотезы |
Решение:
Данное соотношение определяет двустороннюю критическую область, так как двусторонней называют критическую область, определяемую, например, соотношением вида 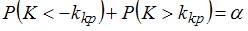 , где
, где 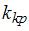 – положительное число, а
– положительное число, а 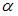 – уровень значимости.
– уровень значимости.
Тема: Элементы корреляционного анализа
Выборочное уравнение прямой линии регрессии 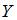 на
на 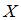 имеет вид
имеет вид 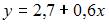 , а выборочные средние квадратические отклонения равны:
, а выборочные средние квадратические отклонения равны: 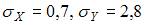 . Тогда выборочный коэффициент корреляции
. Тогда выборочный коэффициент корреляции 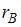 равен …
равен …
 | 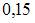 | ||
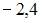 | |||
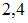 | |||
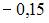 |
Решение:
Выборочный коэффициент корреляции 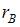 можно вычислить из соотношения
можно вычислить из соотношения 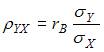 . Тогда
. Тогда 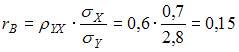 .
.
Тема: Проверка статистических гипотез
Соотношением вида 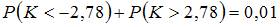 можно определить …
можно определить …
 | двустороннюю критическую область | ||
| правостороннюю критическую область | |||
| левостороннюю критическую область | |||
| область принятия гипотезы |
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 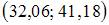 для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
 | 36,62 | ||
| 36,52 | |||
| 9,12 | |||
| 73,24 |
Решение:
Интервальная оценка математического ожидания нормально распределенного количественного признака представляет собой интервал, симметричный относительно точечной оценки. Тогда точечная оценка будет равна 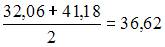 .
.
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 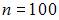 , полигон относительных частот которой имеет вид:
, полигон относительных частот которой имеет вид:
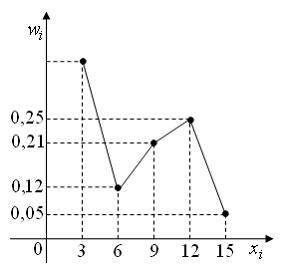
Тогда число вариант 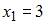 в выборке равно …
в выборке равно …
 | |||
Решение:
Вычислим предварительно относительную частоту варианты 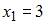 как
как 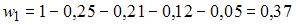 . Тогда из определения относительной частоты
. Тогда из определения относительной частоты 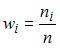 , получаем, что
, получаем, что 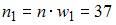
Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема 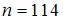 , полигон частот которой имеет вид:
, полигон частот которой имеет вид:
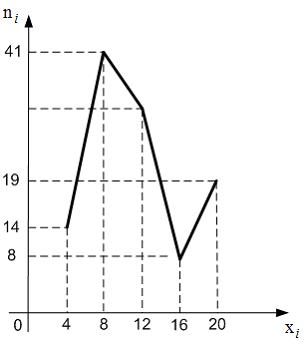
Тогда число вариант 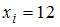 в выборке равно …
в выборке равно …
 | |||
Тема: Проверка статистических гипотез
Соотношением вида 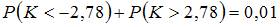 можно определить …
можно определить …
 | двустороннюю критическую область | ||
| правостороннюю критическую область | |||
| левостороннюю критическую область | |||
| область принятия гипотезы |
Тема: Интервальные оценки параметров распределения
Дан доверительный интервал 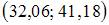 для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …
 | 36,62 | ||
| 36,52 | |||
| 9,12 | |||
| 73,24 |
Тема: Элементы корреляционного анализа
При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции 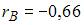 и выборочные средние квадратические отклонения
и выборочные средние квадратические отклонения 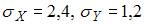 . Тогда выборочный коэффициент регрессии
. Тогда выборочный коэффициент регрессии 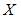 на
на 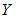 равен …
равен …
 | 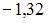 | ||
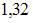 | |||
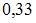 | |||
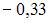 |
Решение:
Выборочный коэффициент регрессии 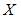 на
на 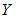 вычисляется по формуле
вычисляется по формуле 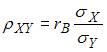 . Тогда
. Тогда 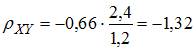
Тема: Статистическое распределение выборки
Статистическое распределение выборки имеет вид

Тогда объем выборки равен …
 | |||
Решение:
Объем выборки вычисляется по формуле 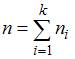 , где
, где 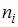 – частота варианты
– частота варианты 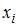 . Тогда
. Тогда 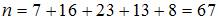 .
.
Тема: Проверка статистических гипотез
Соотношением вида 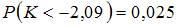 можно определить …
можно определить …
 | левостороннюю критическую область | ||
| правостороннюю критическую область | |||
| двустороннюю критическую область | |||
| область принятия гипотезы |
Решение:
Данное соотношение определяет левостороннюю критическую область, так как левосторонней называют критическую область, определяемую соотношением 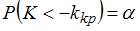 , где
, где 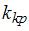 – положительное число, а
– положительное число, а 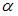 – уровень значимости.
– уровень значимости.
